3.6 De distributiewetten >

Hoofdstukken > Formules

De oppervlakte met en zonder haakjes

Controleer de volgende sommen en zet het rijtje nog een beetje voort. Vreemd toch?

$1 \cdot 2 = 1 + 1$
$2 \cdot 3 = 4 + 2$
$3 \cdot 4 = 9 + 3$
$4 \cdot 5 = 16 + 4$
$5 \cdot 6 = 25 + 5$
........

Bedenk twee sommen die veel verder in de rij zouden voorkomen. Is de uitkomst nog steeds hetzelfde?

Hoe kun je dit nou verklaren? Dat leer je in deze paragaaf.

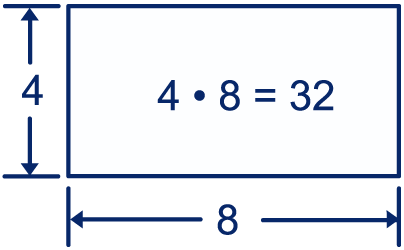
figuur 1

figuur 2

De oppervlakte van figuur 1 kun je eenvoudig vinden. De rechthoek heeft een lengte van 4 en een breedte van 8. De oppervlakte krijg je door de lengte te vermenigvuldigen met de breedte, dus $4 \cdot 8 = 32$ .
In figuur 2 is de lengte 5 en wordt de breedte gegeven door de variabele $a$ . De oppervlakte van deze rechthoek is dan $5 \cdot a$ .

Bepaal de onbekende oppervlaktes en zijde in de rechthoeken.

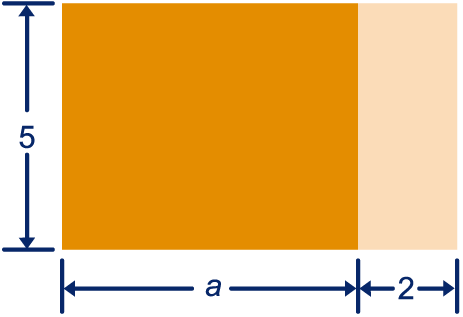
Een rechthoek is verdeeld in een donker en een licht deel. De breedte van het donkere deel is niet bekend; die noemen we $a$ . We gaan de oppervlakte van de rechthoek op twee manieren schrijven.

Neem de onderstaande twee berekeningen over en vul ze in.

1^e manier: lengte $\cdot$ breedte

lengte rechthoek	........
breedte rechthoek	........	$\times$
oppervlakte rechthoek	........

2^e manier: donkere deel $+$ lichte deel

oppervlakte donkere deel	........
oppervlakte lichte deel	........	$+$
oppervlakte rechthoek	........

Je hebt nu de oppervlakte op twee manieren berekend. De twee uitkomsten zijn dus gelijk.

Welke gelijkheid vind je nu?

Je kunt de bovenstaande gelijkheid controleren door enkele getallen in te vullen.

Controleer de gelijkheid voor $a = 7$ en voor $a = 100$ .

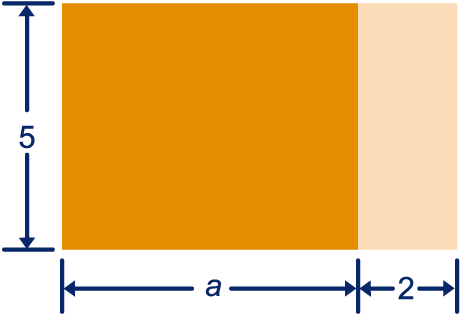
Je kunt de oppervlakte van de rechthoek op twee manieren opschrijven:

met haakjes:	$5 \cdot (a + 2)$
zonder haakjes:	$5 \cdot a + 10$

Deze uitdrukkingen zien er verschillend uit, maar na het invullen van een willekeurig getal voor $a$ geven ze dezelfde uitkomst. Zo krijg je de gelijkheid $5 \cdot (a + 2) = 5 \cdot a + 10$ .

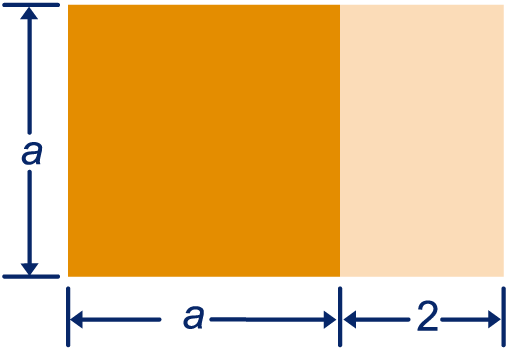
Nogmaals is een rechthoek getekend die is verdeeld in een donker en een licht stuk.

Schrijf de oppervlakte van de rechthoek weer op twee manieren op.

Welke gelijkheid vind je nu?

Controleer de gelijkheid voor $a = 5$ en $a = 10$ .

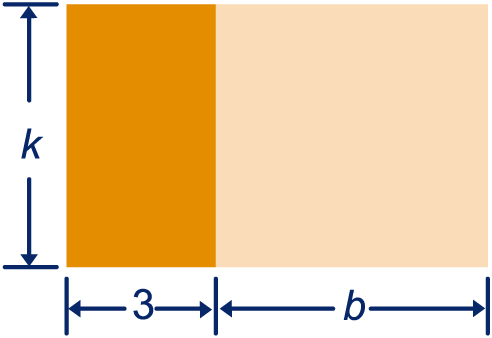
Welke gelijkheid vind je als je de oppervlakte van de afgebeelde rechthoek op twee manieren opschrijft? Vergeet niet je antwoord te controleren.

Je hebt steeds de oppervlakte van rechthoeken op twee manieren geschreven: één keer met haakjes en één keer zonder haakjes. Daaruit kon je dan een gelijkheid opstellen. Zo heb je gezien dat:

$5 \cdot (a + 2) = 5 \cdot a + 10$
$a \cdot (a + 2) = a \cdot a + 2 \cdot a = a^{2} + 2 \cdot a$
$k \cdot (3 + b) = 3 \cdot k + b \cdot k$

figuur 1

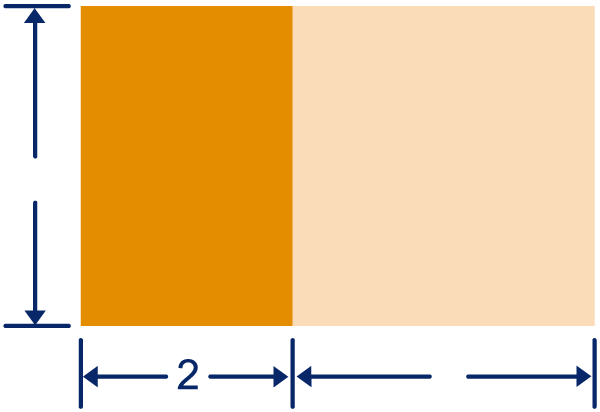
De rechthoek in figuur 1 is verdeeld in twee stukken. De oppervlakte is $3 \cdot (2 + a)$ .

Neem de rechthoek in figuur 1 over en vul de juiste maten in.

Schrijf de oppervlakte van de rechthoek zonder haakjes.

Je hebt nu $3 \cdot (2 + a)$ zonder haakjes geschreven.

Andersom kan ook: iets zonder haakjes met haakjes schrijven.
In de uitdrukking $3 \cdot a + 30$ staan geen haakjes. Het is de oppervlakte van een rechthoek die in twee stukken is verdeeld. De lengte van de rechthoek is 3.

figuur 2

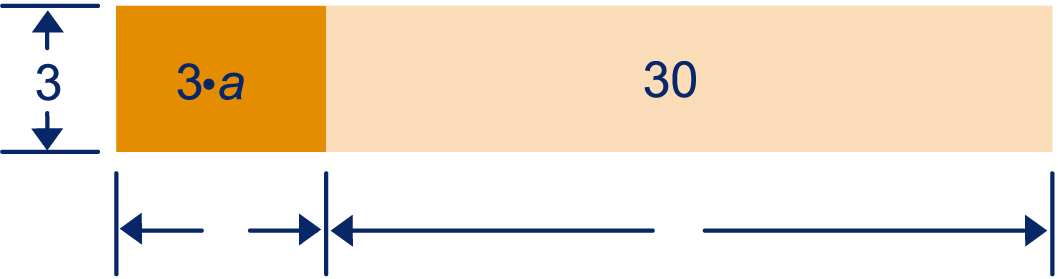
Neem de rechthoek in figuur 2 over en vul de ontbrekende maten in.

Schrijf de oppervlakte van de rechthoek met haakjes.

Oefenen met en zonder haakjes

Schrijf zonder haakjes. Teken er zelf een geschikte rechthoek bij. Als je het zonder rechthoek te tekenen kunt, is dat prima.
$a \cdot (3 + b)$
$(100 + x) \cdot 4$
$k \cdot (99 + k)$

Drie van de uitdrukkingen links zijn gelijk aan drie van de uitdrukkingen rechts, eventueel op een andere regel.

$5 \cdot (n + 10)$	$n^{2} + 10 \cdot n$
$(n + 50) \cdot n$	$5 \cdot n + 50$
$n \cdot (5 + 50)$	$n + 50 \cdot n$
$n \cdot (n + 10)$	$5 \cdot n + 50 \cdot n$
$(n + 5) \cdot 50$	$50 \cdot n + 50$

Schrijf de drie gelijkheden op.

Verander de twee rechts overgebleven uitdrukkingen zodat je nog twee gelijkheden kunt opschrijven.

Verzin er zelf nog twee gelijkheden bij.

Neem de opgaven over en vul de lege plekken in.

$3 \cdot a + 12 =$	$3 \cdot a + 3 \cdot ... =$	$3 \cdot (... + ...)$
$7 \cdot a + 35 =$	$7 \cdot a + 7 \cdot ... =$	$7 \cdot (... + ...)$
$a \cdot b + 3 \cdot a =$	$a \cdot b + a \cdot 3 =$	$a \cdot (... + ...)$

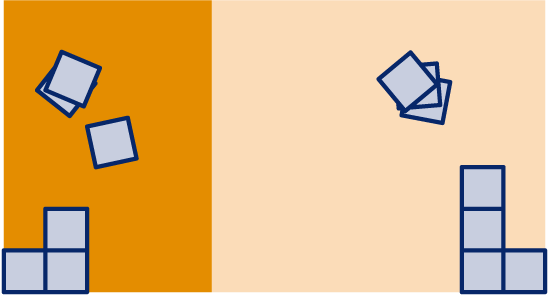
Een rechthoekig terras is geheel geplaveid met tegels van $1$ bij $1$ meter. Op het linker stuk liggen $35$ tegels, op het rechterstuk liggen $56$ tegels.

Wat zijn de lengte en de breedte van het terras? Schrijf op hoe je aan je antwoord gekomen bent.

11s

Paul en Hans krijgen dezelfde twee getallen. De getallen moeten gekwadrateerd en opgeteld worden. Paul kwadrateert de getallen eerst en telt ze dan bij elkaar op. Hans telt de getallen eerst op en kwadrateert het resultaat.

Leg uit waarom Hans altijd de grootste uitkomst krijgt. Teken geschikte vierkanten om dit te laten zien.

(hint)

Noem de getallen $a$ en $b$ en maak tekeningen bij de bewerkingen $a^{2} + b^{2}$ en ${(a + b)}^{2}$ .

De distributiewetten

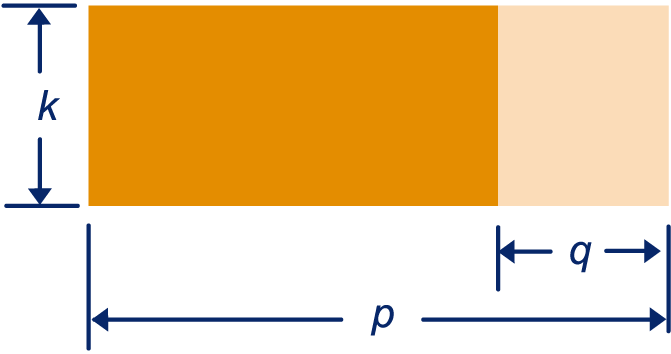
Een rechthoek is verdeeld in twee stukken: een donker en een licht stuk. De lengte van de rechthoek is $k$ en de totale breedte is $p$ . De breedte van het lichte stuk is $q$ .
We gaan de oppervlakte van het donkere stuk op twee manieren schrijven.

Neem de onderstaande twee berekeningen over en vul ze in.

1^e manier: lengte $\cdot$ breedte

lengte donkere deel	........
breedte donkere deel	........ $\times$ ........
oppervlakte donkere deel	........

2^e manier: totale oppervlakte $-$ lichte deel

totale oppervlakte	........
oppervlakte lichte deel	........ $-$ ........
oppervlakte donkere deel	........

Welke gelijkheid kun je nu opschrijven?

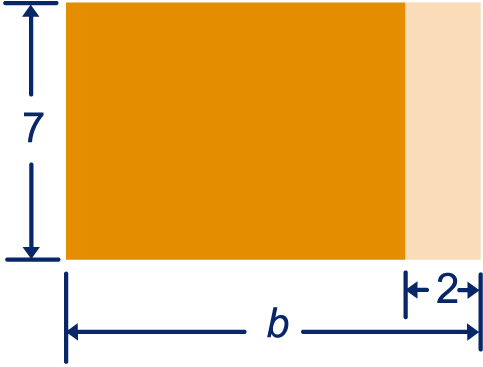
De lengte van een rechthoek is $7$ . De breedte van de hele rechthoek is $b$ . Het lichte deel heeft breedte $2$ . De oppervlakte van het donkere deel is dan $7 \cdot (b - 2)$ .
Schrijf de oppervlakte van het donkere deel ook zonder haakjes.

Schrijf zonder haakjes. Teken er een geschikte rechthoek bij als je dat handig vindt. Kun je het zonder rechthoek, dan is het ook prima.
$7 \cdot (b - 5)$
$k \cdot (8 - p)$

Neem de opgaven over en vul de lege plekken in.

$4 \cdot a - 40 =$	$4 \cdot a - 4 \cdot ... =$	$4 \cdot (... - ...)$
$a^{2} - 3 \cdot a =$	$a \cdot a - a \cdot ... =$	$a \cdot (... - ...)$
$a \cdot b - 3 \cdot a =$	$a \cdot b - a \cdot ... =$	$a \cdot (... - ...)$

Je hebt nu twee gelijkheden leren kennen:
$a \cdot (b + c) = a \cdot b + a \cdot c$
$a \cdot (b - c) = a \cdot b - a \cdot c$
Deze gelijkheden heten distributiewetten. Distributie komt van het werkwoord distribueren en dat betekent verdelen.

In de bovenstaande gelijkheden stellen $a$ , $b$ en $c$ getallen voor. In de tweede gelijkheid moet het getal $c$ kleiner zijn dan het getal $b$ .

Leg uit waarom.

We gaan de gelijkheid $a \cdot (b + c) = a \cdot b + a \cdot c$ eens nader bekijken. Neem eens voor $a$ het getal 4, voor $b$ het getal 8 en voor $c$ het getal 3.

Welk getal staat er dan links van het $=$ -teken? En rechts? Klopt dat?

Je hebt nu de gelijkheid $a \cdot (b + c) = a \cdot b + a \cdot c$ gecontroleerd voor $a = 4$ , $b = 8$ en $c = 3$ .

Controleer de gelijkheid $a \cdot (b - c) = a \cdot b - a \cdot c$ voor $a = 10$ , $b = 18$ en $c = 8$ .

De distributiewetten zien er misschien wat moeilijk uit, maar eigenlijk pas je deze wetten al jaren (onbewust) toe. Bijvoorbeeld als je $13 \cdot 25 + 7 \cdot 25$ en $6 \cdot 101$ uit je hoofd uitrekent.

Voorbeeld:

Voorbeelden

$13 \cdot 25 + 7 \cdot 25 = 25 \cdot (13 + 7) = 25 \cdot 20 = 500$
$6 \cdot 101 = 6 \cdot (100 + 1) = 6 \cdot 100 + 6 \cdot 1 = 600 + 6 = 606$

Maak zo ook de volgende sommen. Bij de sommen waar de variabele $a$ in voorkomt, blijft in je antwoord de variabele $a$ staan. Schrijf een tussenstap op.

$98 \cdot 25 + 2 \cdot 25 = ... \cdot (... + ...) = ........$
$11 \cdot a + 89 \cdot a$
$1 \cdot 29 + 2 \cdot 29 + 3 \cdot 29 + 4 \cdot 29$
$1 \cdot a + 2 \cdot a + 3 \cdot a + 4 \cdot a$

$39 \cdot 25 - 19 \cdot 25 = ... \cdot (... - ...) = ........$
$51 \cdot 25 - 11 \cdot 25$
$765 \cdot a - 760 \cdot a$
$123 \cdot a - 20 \cdot a - 3 \cdot a$

$17 \cdot 99 = ... \cdot (... - ...) = ........$
$9 \cdot 1005$
$19 \cdot 998$

17s

18s

Bereken de volgende som op een handige manier.
$1 \cdot 50 + 2 \cdot 50 + 3 \cdot 50 + \dots + 29 \cdot 50 + 30 \cdot 50 =$

Oefenen met de distributiewetten

Schrijf zonder haakjes zo eenvoudig mogelijk.

$4 \cdot (a + 5)$	$3 \cdot (x + a - 2)$
$(p - 3) \cdot a$	$(3 - x + 2) \cdot x$

Neem de opgaven over en vul de lege plekken in

$... \cdot (x + 2) = 7 \cdot x + 14$	$4 \cdot (x - ...) = ..... - 4$
$... \cdot (x - ...) = 2 \cdot x - 10$	$... \cdot (... + ...) = 5 \cdot a + 5 \cdot b$
$... \cdot (x - 4) = ..... - 20$	$... \cdot (... + ...) = x^{2} + 6 \cdot x$

In opgave 15 heb je formules verzonnen bij onderstaande rooster.

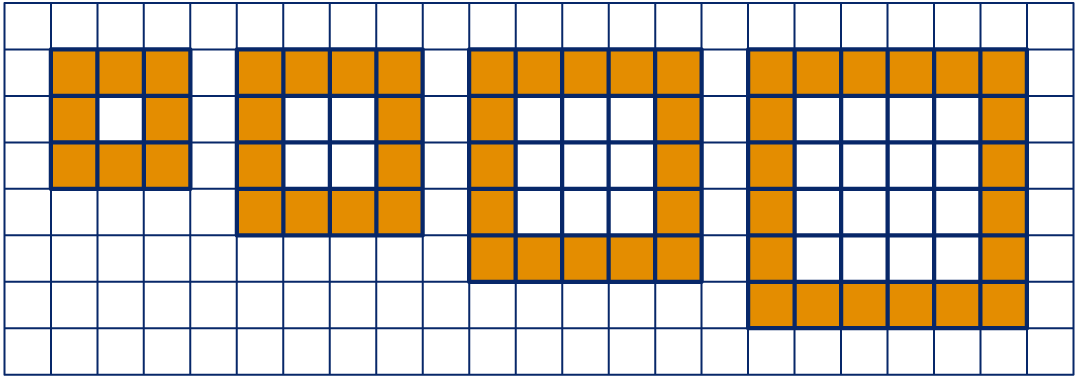
De letter O is in allerlei groottes gekleurd. De breedte $b$ van de letters varieert van 3 tot 6. Ines heeft de volgende formule verzonnen voor het aantal gekleurde hokjes $H$ :
$H = 4 \cdot (b - 2) + 4$
Schrijf deze formule zonder haakjes zo eenvoudig mogelijk. Controleer of de formule die je zo gevonden hebt, klopt.

Bedenk drie opgaven die je maatje op moet lossen. In de opgaven moeten de distributiewetten voorkomen. Jij lost de opgaven op die je van je maatje hebt gekregen.

In opgave 22 heb je kennis gemaakt met de onderstaande, vreemde rij. Probeer een verklaring te vinden voor deze rij.

$1 \cdot 2 = 1 + 1$
$2 \cdot 3 = 4 + 2$
$3 \cdot 4 = 9 + 3$
$4 \cdot 5 = 16 + 4$
$5 \cdot 6 = 25 + 5$
........

(hint)

Noem de twee getallen die met elkaar worden vermenigvuldigd $n$ en $n + 1$ . Teken een plaatje bij deze vermenigvuldiging.

Opmerking:

Wil je nog extra oefenen, bijvoorbeeld met een spelletje, dan kan dit met de applet memory: oppervlakteformules .
Het leukst is de optie 'trio's', want dan moet je telkens de drie dingen zoeken die bij elkaar horen: een plaatje, een formule met haakjes en een formule zonder haakjes.

Of je speelt de digitale mini-loco: mini-loco: distributiewet .