Van de cirkel zijn delen van $\frac{1}{3}$ en $\frac{1}{6}$ aangegeven.

Uit het plaatje kun je aflezen dat $\frac{1}{3} + \frac{1}{6} = \frac{1}{2}$ .

Maak ook een plaatje bij elk van de volgende optellingen. Gebruik verschillende kleuren. Schrijf de som als één breuk, zo eenvoudig mogelijk.

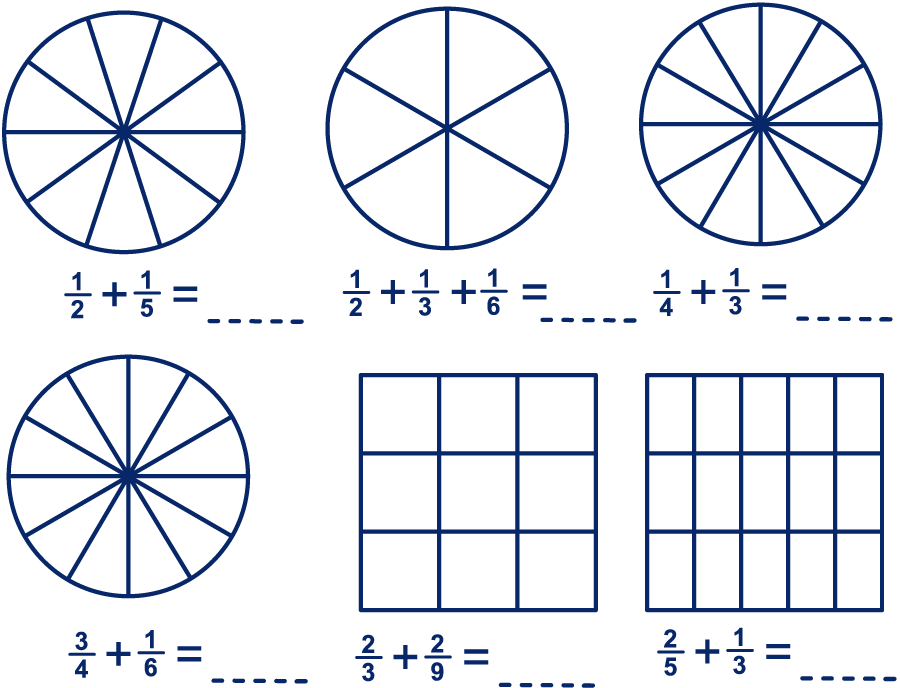
Voor $\frac{1}{2} + \frac{1}{5}$ verdeelden we de cirkel in tienden.

Vul de redenering verder in.
$\frac{1}{2}$ is ..... tienden; $\frac{1}{5}$ is ..... tienden.
Kort opgeschreven: $\frac{1}{2} + \frac{1}{5} = \frac{...}{10} + \frac{...}{10} = \frac{...}{10}$ .

Als je $\frac{1}{2} + \frac{1}{7}$ wilt berekenen, in hoeveel stukjes zou je de cirkel dan verdelen?

Maak de redenering af.
$\frac{1}{2} + \frac{1}{7} = ..... + ..... = .....$

Als je $\frac{1}{2} + \frac{1}{6}$ zou willen berekenen, in hoeveel stukjes zou je de cirkel dan verdelen?

Bereken op dezelfde manier. Schrijf je antwoord zo eenvoudig mogelijk. Schrijf ook je tussenstappen op ( $p$ en $q$ zijn variabelen).

$\frac{2}{3} + \frac{1}{12}$	$\frac{p}{5} + \frac{1}{2}$
$\frac{3}{7} - \frac{1}{4}$	$\frac{1}{5} - \frac{1}{7}$
$\frac{1}{2} - \frac{1}{4} + \frac{1}{5}$	$\frac{4}{5} - \frac{3}{7}$
$\frac{2}{5} + \frac{1}{2}$	$\frac{3}{5} - \frac{q}{7}$
$\frac{4}{5} + \frac{1}{2}$

De Egyptenaren in de oudheid kenden alleen stambreuken. Dat zijn breuken met teller 1; dus $\frac{1}{2}$ , $\frac{1}{3}$ , $\frac{1}{4}$ , enzovoorts.
In het plaatje kun je goed zien dat het verschil tussen twee opvolgende stambreuken kleiner is, naarmate de noemer groter is.

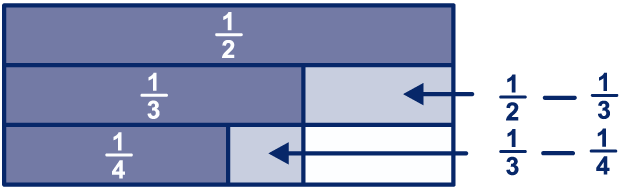
Je ziet: $\frac{1}{2} - \frac{1}{3} > \frac{1}{3} - \frac{1}{4}$
Schrijf zo eenvoudig mogelijk.

$1 - \frac{1}{2}$	$\frac{1}{4} - \frac{1}{5}$
$\frac{1}{2} - \frac{1}{3}$	$\frac{1}{5} - \frac{1}{6}$
$\frac{1}{3} - \frac{1}{4}$	$\frac{1}{99} - \frac{1}{100}$

De Egyptenaren schreven in plaats van $\frac{3}{4}$ een $\frac{1}{2} + \frac{1}{4}$ , in plaats van $\frac{11}{12}$ schreven zij $\frac{1}{2} + \frac{1}{3} + \frac{1}{12}$ .

Controleer of dit laatste goed is.

Schrijf als som van verschillende stambreuken.

$\frac{3}{8} = ..... + .....$	$\frac{4}{5} = \frac{1}{2} + ..... + .....$
$\frac{4}{9} = ..... + .....$	$\frac{11}{15} = \frac{1}{2} + ..... + .....$

Bereken de volgende sommen ( $p$ en $q$ zijn variabelen).

$\frac{4}{5} + \frac{1}{2}$	$\frac{1}{5} - \frac{1}{7}$
$\frac{p}{5} + \frac{1}{2}$	$\frac{1}{5} - \frac{q}{7}$
$\frac{p}{5} + \frac{p}{2}$	$\frac{q}{5} - \frac{q}{7}$

Als je breuken bij elkaar optelt of van elkaar aftrekt, moet je er voor zorgen dat de noemers gelijk zijn. We zeggen dan dat we de breuken eerst gelijknamig maken.

Voor verder oefenen met het optellen en aftrekken van breuken ga je naar de website de Wageningse Methode, kies software Basisvorming 1 en ga naar Oefenen met Breuken. Voor optellen en aftrekken neem je "Hoeveel zijn de breuken samen?" en "Hoeveel verschillen de breuken?".
Er zijn ook een aantal digitale mini-loco's die je kunt maken.

Voor een instructiefilmpje van Leerlingen voor leerlingen over optellen van breuken ga je naar Optellen van breuken.

Optellen en aftrekken kan ook met variabelen. Hieronder staan twee voorbeelden.

$\frac{2}{a} + \frac{3}{7} = \frac{14}{7 a} + \frac{3 a}{7 a} = \frac{14 + 3 a}{7 a}$

$\frac{2 a}{3} - \frac{a}{5} = \frac{10 a}{15} - \frac{3 a}{15} = \frac{7 a}{15}$

Maak zo zelf de volgende sommen.

$\frac{a}{3} + \frac{a}{9}$	$\frac{3}{a} + \frac{9}{a}$
$\frac{5 a}{6} + \frac{a}{9}$	$\frac{3}{a} + \frac{2}{5}$
$\frac{a}{3} - \frac{2 a}{9}$	$\frac{3 a}{a} - \frac{1}{2}$
$\frac{4 a}{3} - \frac{5 a}{9}$	$\frac{2}{7} - \frac{1}{a}$

Elk van de linker figuren heeft steeds oppervlakte 1. In het rechter plaatje is het deel aangegeven dat gekleurd is.

Hier zie je zes andere figuren met oppervlakte 1.

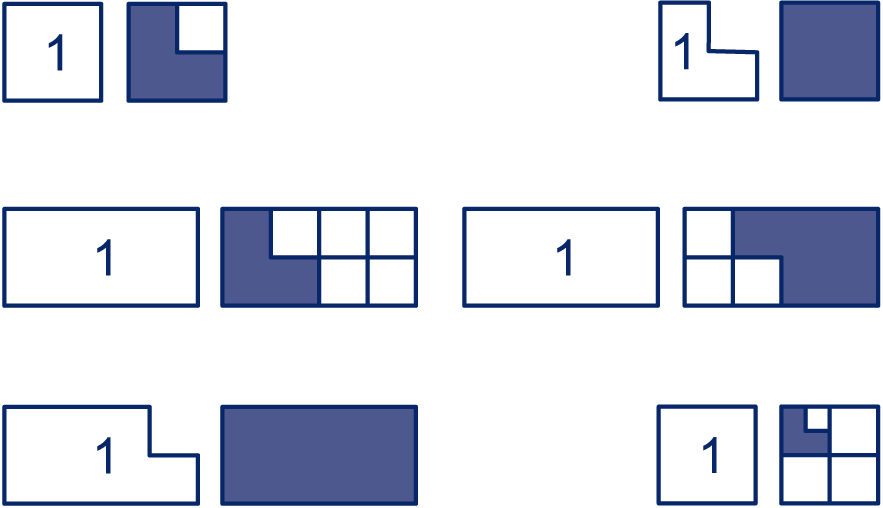
Geef aan welk deel telkens in de rechter figuur gekleurd is.

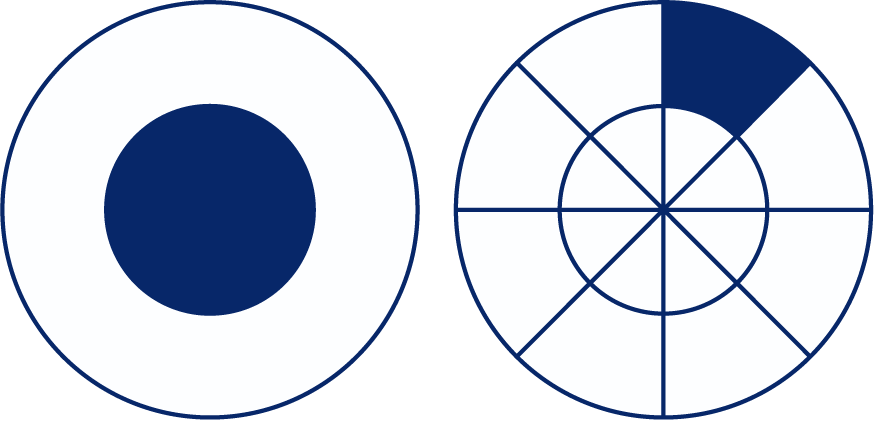
Van de linker cirkel is $\frac{1}{4}$ deel gekleurd.

Welk deel van de rechter cirkel is gekleurd?

Bereken ook welk deel van de driehoek en het vierkant gekleurd is.