Soorten driehoeken

Een driehoek met een rechte hoek noemen we een rechthoekige driehoek.

Teken een rechthoekige gelijkbenige driehoek met twee zijden van 4 cm.

Teken een gelijkbenige driehoek met een zijde van 3 cm en een zijde van 5 cm.
Er zijn twee mogelijkheden.

Teken een rechthoekige driehoek met een zijde van 3 cm en een zijde van 5 cm.
Er zijn twee mogelijkheden.

Teken een driehoek $A B C$ met $∠ A = 35 °$ . Maak $A B = 5$ cm en $A C = 3$ cm.

Teken een driehoek $K L M$ met $∠ K = 35 °$ .
Maak $K L = 5$ cm. Zorg ervoor dat $L M = 3$ cm; daarbij kun je je passer goed gebruiken. Er zijn twee mogelijke plaatsen voor $M$ .

Teken een driehoek met een hoek van $35 °$ en zijden van 4 en 5 cm. Er zijn drie verschillende mogelijkheden; teken ze alledrie.

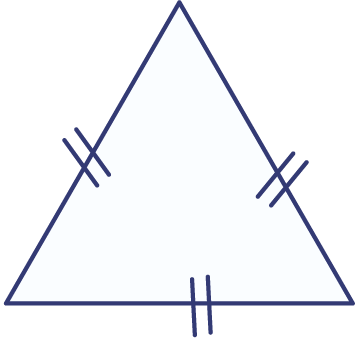
Een driehoek met drie gelijke zijden heet een gelijkzijdige of regelmatige driehoek.

Wat weet je van de hoeken van een gelijkzijdige driehoek?

Hoeveel scherpe hoeken kan een driehoek hebben?

Hoeveel rechte hoeken kan een driehoek hebben?

Hoeveel stompe hoeken kan een driehoek hebben?

In een driehoek zijn altijd twee hoeken scherp.
Als de derde hoek ook scherp is, dan noemen we de driehoek scherphoekig.
Als de derde hoek recht is, noemen we de driehoek rechthoekig.
Als de derde hoek stomp is, noemen we de driehoek stomphoekig.

Waar of niet waar?

Elke gelijkzijdige driehoek is scherphoekig.

Elke gelijkbenige driehoek is scherphoekig.

Elke driehoek kun je verdelen in twee rechthoekige driehoeken.

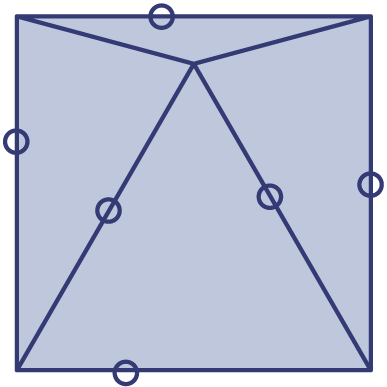
Een vierkant is verdeeld in vier driehoeken. Gelijke zijden zijn met eenzelfde teken aangegeven.

Zeg van elk van de vier driehoeken of hij gelijkbenig/gelijkzijdig is en ook of hij scherphoekig/rechthoekig/stomphoekig is.

De driehoeken hebben in totaal twaalf hoeken. Sommige hoeken zijn gelijk.

Van hoeveel verschillende groottes zijn de hoeken?

Een ladder van 5 meter staat tegen een muur. De voet van de ladder staat 1 meter van de muur af.

Teken het zijaanzicht op schaal $1 : 100$ .

Meet hoe groot de hoek is die de ladder met de grond maakt.

Meet hoe hoog de ladder tegen de muur reikt.

Een sluis is 9 meter breed. De twee sluisdeuren zijn elk 5 meter. Als de sluisdeuren dicht zijn, maken ze een stompe hoek met elkaar.

Teken het bovenaanzicht op schaal.

Meet hoe groot de hoek is die de sluisdeuren met elkaar maken.

10s

Waar of niet waar?

Elke driehoek kun je verdelen in twee scherphoekige driehoeken.

Elke driehoek kun je verdelen in twee stomphoekige driehoeken.

Elke driehoek kun je verdelen in drie stomphoekige driehoeken.

Elke driehoek kun je verdelen in drie gelijkbenige driehoeken.

Elke rechthoekige driehoek kun je verdelen in twee gelijkbenige driehoeken.

11s

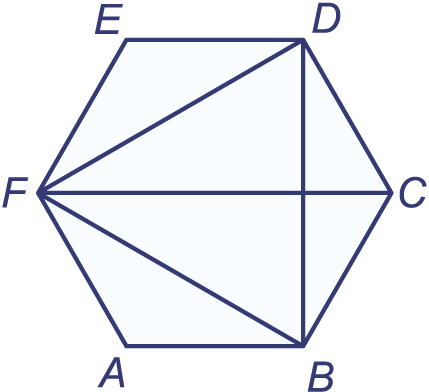
$A B C D E F$ is een regelmatige zeshoek. Er zijn vier diagonalen getekend.

Zeg van elk van de volgende driehoeken of hij gelijkbenig/gelijkzijdig en ook of hij scherphoekig/rechthoekig/stomphoekig is: $A B F$ , $B D F$ , $B C F$ .

$A B C D E F G H$ is een kubus. $M$ is het midden van $B F$ .

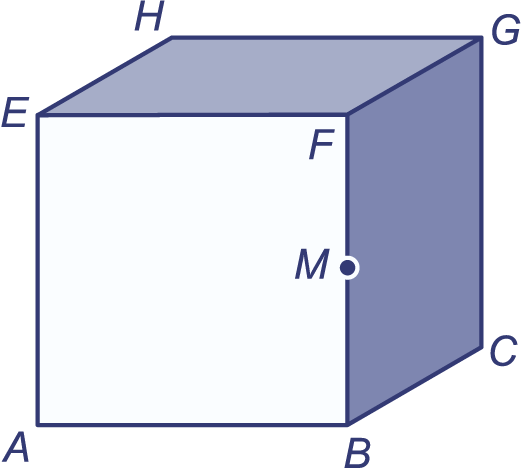
Zeg van elk van de volgende driehoeken of hij gelijkbenig/gelijkzijdig en scherphoekig/rechthoekig/stomphoekig is: $A B C$ , $A M C$ , $B C G$ , $B G E$ , $E H M$ .

Kijklijnen

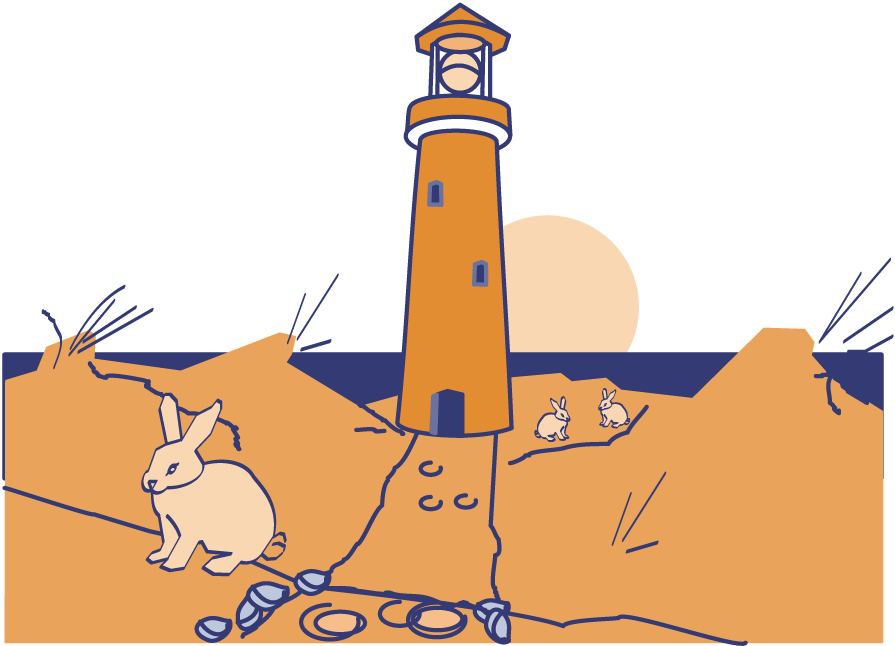
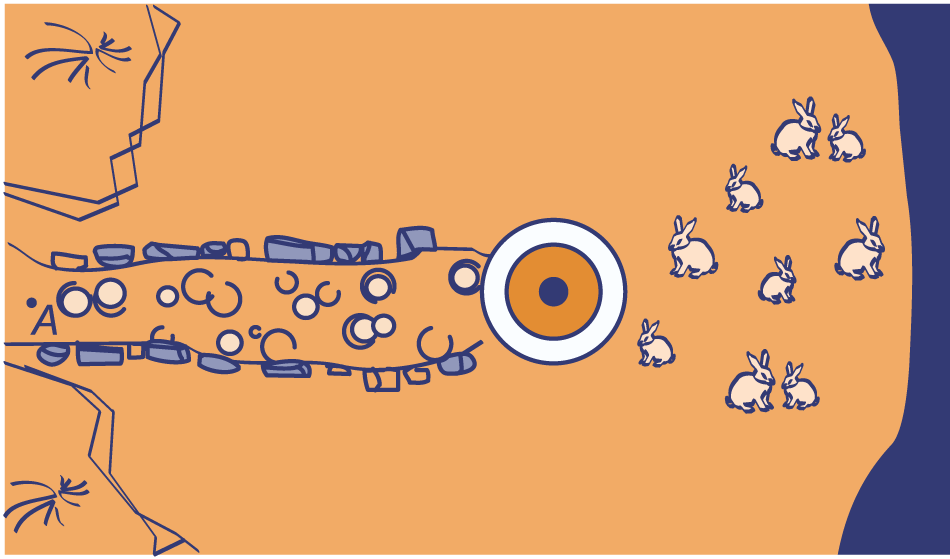
De vuurtorenwachter loopt naar de vuurtoren. Achter de toren spelen konijntjes in het gras. Ze lopen niet meer weg voor de vuurtorenwachter. Het tweede plaatje is een bovenaanzicht. Daarin kun je zien waar de konijntjes op een gegeven moment zitten.

Laat in applet Vuurtorenwachter zien hoeveel konijntjes hij kan zien.
Hoe groot is dan de hoek tussen de kijklijnen?

Thuis vertelt de vuurtorenwachter: "Als ik naar de toren loop, kom ik steeds dichter bij de konijntjes. Ze lopen niet weg. Toch zie ik steeds minder konijntjes."

Hoe komt dat? Leg dat met het tweede plaatje uit.

Als de vuurtorenwachter dicht genoeg bij de vuurtoren komt, ziet hij vanaf een bepaalde plek helemaal geen konijntjes meer.

Zoek dat punt in applet Geen konijntjes meer. Hoe groot is dan de hoek tussen de linker en rechter kijklijn langs de vuurtoren?

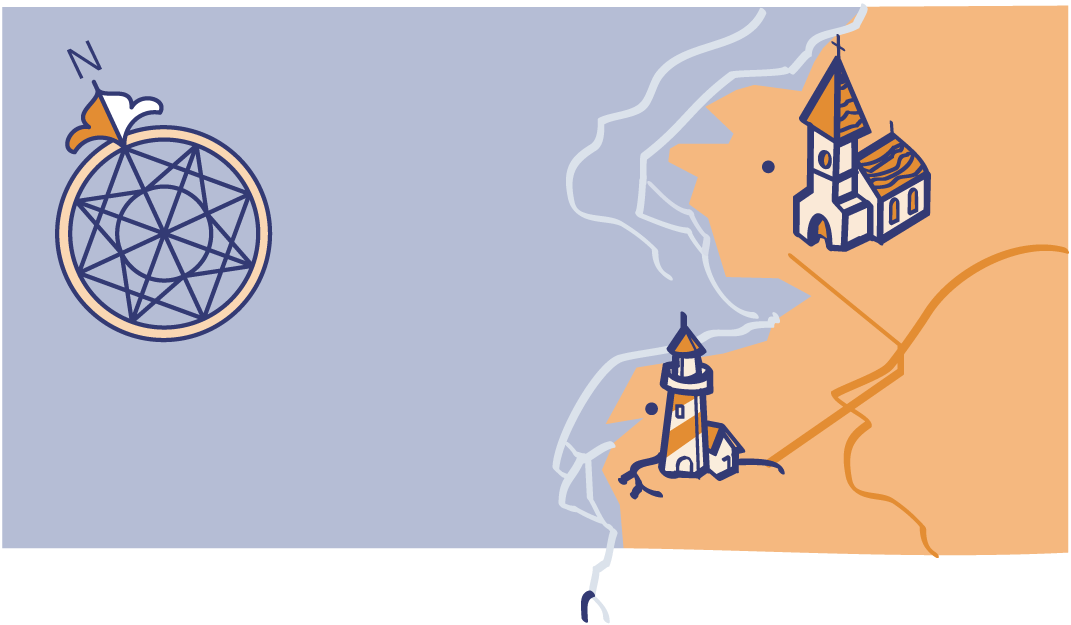
Op een eiland is de precieze plaats van de vuurtoren met een stip aangegeven en ook de precieze plaats van de kerk. Links op het kaartje is een windroos getekend. De pijl wijst naar het noorden.

Op zee, in de buurt van dit eiland, vaart een boot. Als de stuurman naar het oosten kijkt, ziet hij de kerktoren. Als de stuurman naar het zuidoosten kijkt, ziet hij de vuurtoren.

Geef in applet Boot - door twee lijnen te tekenen - de plaats van het schip aan.

Ronnie woont op dit eiland. Als hij vanuit zijn huis naar het noorden kijkt, ziet hij de kerk. Als hij naar het noordwesten kijkt, ziet hij de vuurtoren.

Geef in applet Huis de plaats aan waar Ronnie woont.

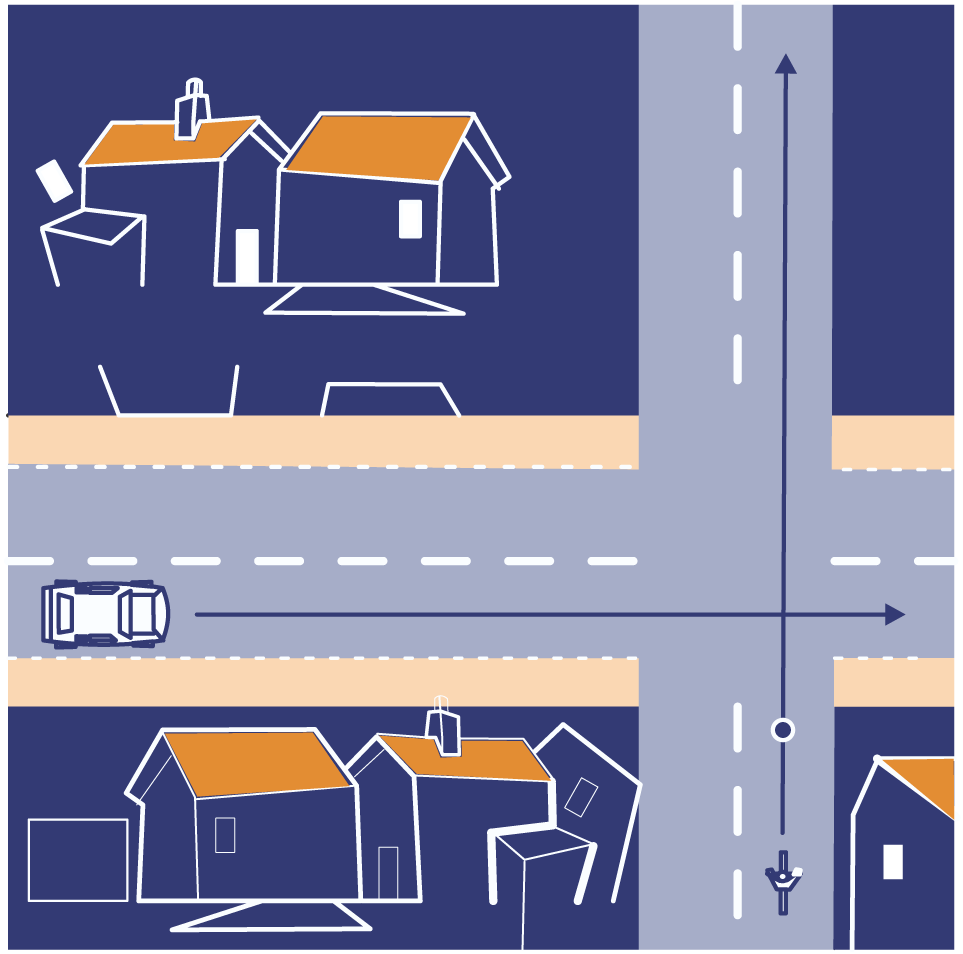
Een auto en een fiets naderen een gevaarlijke kruising. De kruising is zo gevaarlijk door de dichte bebouwing langs de wegen. Ze willen allebei recht door.

In het plaatje zie je waar de auto en de fiets zich op een bepaald moment bevinden.

Zien ze elkaar op dat moment? Waarom (niet)?

Meet op het werkblad hoe groot de kijkhoek van de fietser op dat moment is. Dat is de hoek tussen de meest linkse en meest rechtse kijklijn die niet door de bebouwing wordt tegengehouden.

De fiets rijdt 20 km/u en de auto 50 km/u.

Geef op het werkblad aan waar de voorkant van de auto is als de voorkant van de fiets bij de plek is die met het rondje is aangegeven.
Zien ze elkaar nu?

Veronderstel dat ze geen van beiden opletten en gewoon hun weg vervolgen zonder vaart te minderen.

Krijgen we een botsing?

In de applet Blikveld van een fietser kun je dit uitvoeren.

14s

15s

figuur 1

In figuur 1 is $K$ de plaats van de kerktoren. Er is ook een vuurtoren $V$ . Ad staat bij plaats $A$ ; de richtingen vanuit $A$ naar $K$ en naar $V$ maken een hoek van $30 °$ met elkaar. Bea staat bij plaats $B$ ; de richtingen vanuit $B$ naar $K$ en naar $V$ maken een hoek van $20 °$ met elkaar.

Er zijn vier mogelijke plaatsen voor $V$ die aan deze gegevens voldoen. Eén ervan zie je in figuur 2.

figuur 2

Teken op het werkblad de andere drie mogelijkheden voor de plaats van de vuurtoren.