Omgeschreven cirkel

Teken op een blaadje een scherphoekige driehoek. Noem de hoekpunten $A$ , $B$ en $C$ .

Vouw heel precies de middelloodlijn van zijde $A B$ en ook van zijde $B C$ .

Het snijpunt van de twee middelloodlijnen noemen we $M$ .

Teken de cirkel met middelpunt $M$ die door $A$ gaat.

Als je precies gewerkt hebt, lijkt de cirkel ook door $B$ en $C$ te gaan.
Dat de cirkel door $B$ en $C$ moet gaan, kunnen we beredeneren. Daarvoor moet je begrijpen dat $M A = M B = M C$ .

Waarom geldt: $M A = M B$ ?

Waarom geldt: $M B = M C$ ?

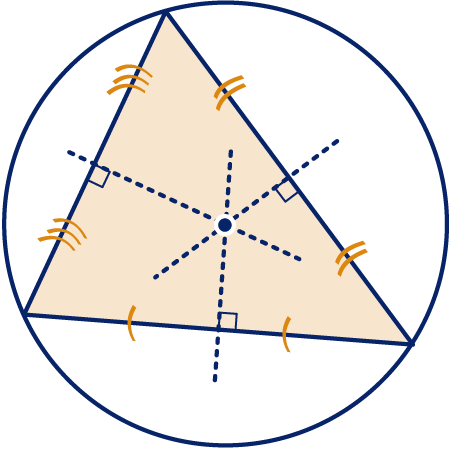
Uit d en e volgt dat $M A = M B = M C$ , dus dat de cirkel met middelpunt $M$ zowel door $A$ , $B$ als $C$ gaat. Tevens volgt hieruit dat $M$ op de middelloodlijn van $A C$ ligt. $M$ is dus het snijpunt van de drie middelloodlijnen.

Teken een op een blaadje een stomphoekige driehoek $A B C$ .

Vouw de middelloodlijnen van twee zijden (zoals in de vorige opgave). Noem het snijpunt van de twee vouwlijnen $M$ .

Teken de cirkel met middelpunt $M$ die door $A$ gaat. Deze cirkel gaat ook door $B$ en $C$ .

Teken een scherphoekige driehoek.

Zoek het middelpunt van de omgeschreven cirkel van de driehoek door twee middelloodlijnen te tekenen met je geodriehoek.

Teken de omgeschreven cirkel van de driehoek.

Teken een stomphoekige driehoek.

Teken de omgeschreven cirkel van de driehoek. Ga net zo te werk als in de vorige opgave.

Bij elke rechthoek kun je een cirkel tekenen die door de vier hoekpunten van de rechthoek gaat.

Waar ligt het middelpunt van deze cirkel?

Het middelpunt van de omgeschreven cirkel van een rechthoekige driehoek is het midden van de schuine zijde.

Hoe kun je dat uit onderdeel a beredeneren?

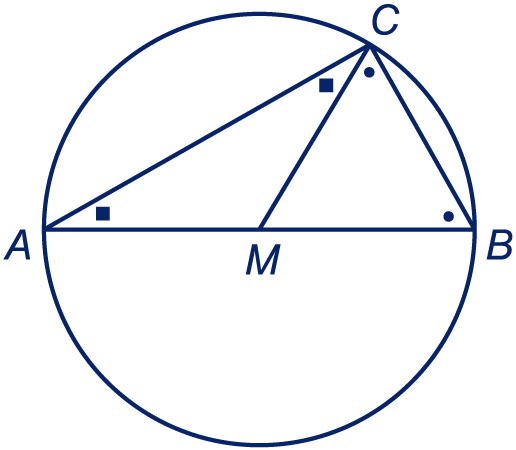
$M$ is het middelpunt van de omgeschreven cirkel van driehoek $A B C$ . $M$ ligt op zijde $A B$ .

Waarom zijn de hoeken $M A C$ en $M C A$ even groot? En waarom zijn de hoeken $M B C$ en $M C B$ even groot?

De twee hoeken bij $C$ zijn dus samen de helft van de vier hoeken waar een tekentje in staat.

Hoe groot is dus hoek $A C B$ ?

In onderdeel b heb je gezien dat het middelpunt van de omgeschreven cirkel van een rechthoekige driehoek het midden van de schuine zijde is. Het omgekeerde is dus ook waar: als het middelpunt van de omgeschreven cirkel van een driehoek op een zijde ligt, is de driehoek rechthoekig. Dat heb je in d gezien.

Ingeschreven cirkel

Teken op een blaadje driehoek $A B C$ ,
met $A B = 8$ cm, $B C = 6$ cm en $A C = 10$ cm.

Vouw heel precies de deellijn van hoek $A$ en ook van hoek $B$ . Noem het snijpunt van de vouwlijnen $M$ .

Teken met de geodriehoek de loodlijn vanuit $M$ op zijde $A B$ . Noem het snijpunt van zijde $A B$ met deze loodlijn $P$ en teken de cirkel met middelpunt $M$ die door $P$ gaat.

Als je precies gewerkt hebt, lijkt de cirkel niet alleen zijde $A B$ te raken, maar ook de andere twee zijden van driehoek $A B C$ .
Dat komt omdat $M$ even ver van de zijden van driehoek $A B C$ af ligt. Dat beredeneren we in de volgende onderdelen.

Waarom ligt $M$ even ver van zijde $A B$ als zijde $B C$ ?

Waarom ligt $M$ even ver van zijde $A B$ als zijde $A C$ ?

Uit d en e volgt dat $M$ even ver van de zijden van driehoek $A B C$ af ligt en dus dat de cirkel alle zijden van driehoek $A B C$ raakt. Tevens volgt hieruit dat de deellijn van hoek $C$ ook door $M$ gaat.

Elke driehoek heeft een omgeschreven cirkel.

Dat is de cirkel die door de hoekpunten van de driehoek gaat.

De drie middelloodlijnen van de zijden van de driehoek gaan door het middelpunt van de omgeschreven cirkel.

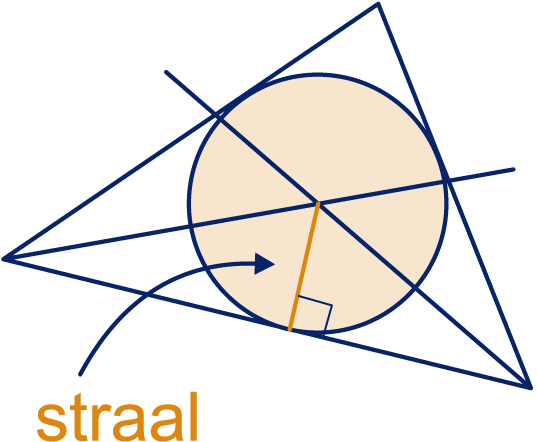
Elke driehoek heeft een ingeschreven cirkel. Dat is de cirkel die de zijden van de driehoek raakt.

De deellijnen van de hoeken van de driehoek gaan door één punt. Dit punt is het middelpunt van de ingeschreven cirkel. Als je de cirkel wilt tekenen, moet je eerst de straal vinden. Laat vanuit het middelpunt een loodlijn neer op één van de zijden, dan is dat de straal.

Uit de lap stof in het plaatje moet een zo groot mogelijk rond kleed geknipt worden.

Bepaal het middelpunt van het kleed.

Teken de cirkel waarlangs je het kleed moet knippen.

Van een gelijkbenige driehoek $A B C$ is gegeven $A B = 8$ cm en $∠ A = ∠ B = 56 °$ .

Teken de driehoek.

Teken met de geodriehoek de drie deellijnen van de hoeken.

Teken de ingeschreven cirkel van driehoek $A B C$ .

Boer Jansen heeft een driehoekig stuk weiland. Daarop wil hij zijn geit laten grazen. Die geit zit met een touw vast aan een paaltje. Het touw maakt hij zo lang dat de geit niet buiten de wei kan grazen. De boer wil de geit een zo groot mogelijk stuk van de wei laten afgrazen.

Teken op het werkblad de plaats waar de boer het paaltje in de grond moet slaan.

Kleur het gebied dat de geit kan afgrazen.

10s

In driehoek $A B C$ is $∠ A = 50 °$ en $∠ B = 60 °$ . Het middelpunt van de ingeschreven cirkel noemen we $M$ .

Maak een schets van de situatie.

Door $M$ met $A$ , $B$ en $C$ te verbinden, krijg je bij $M$ drie hoeken (die samen $360 °$ zijn).

Bereken hoe groot die hoeken zijn.

11s

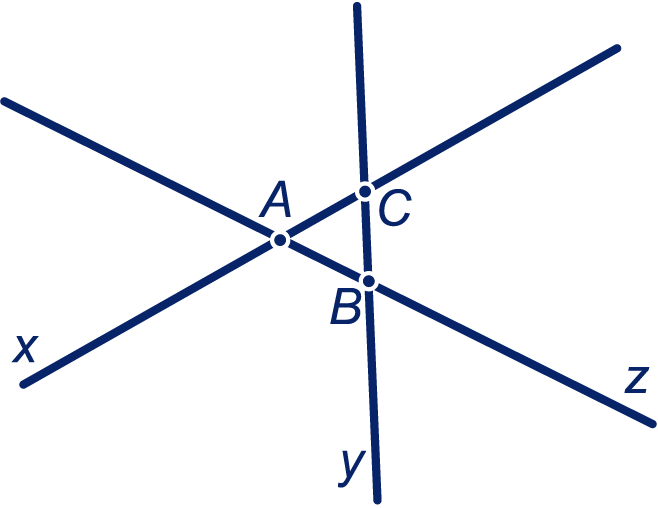
De drie lijnen $x$ , $y$ en $z$ snijden elkaar in de punten $A$ , $B$ en $C$ . De ingeschreven cirkel van driehoek $A B C$ raakt aan alle drie de lijnen $x$ , $y$ en $z$ .
Er zijn nog meer cirkels te tekenen die aan alle drie de lijnen raken.

Teken heel precies de middelpunten van deze cirkels. Licht toe hoe je ze gevonden hebt.

Teken de cirkels.

Op het werkblad is een cirkel getekend.

Zoek het middelpunt van die cirkel. Schrijf op hoe je te werk bent gegaan.