1

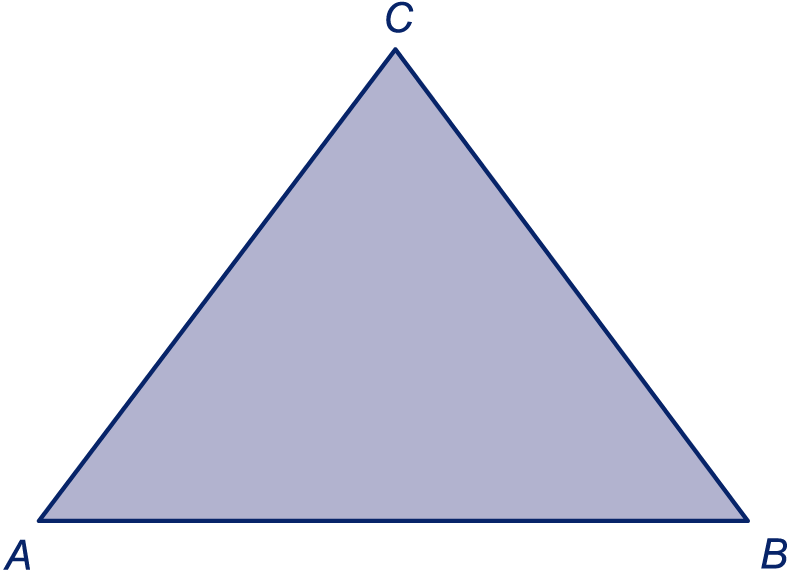
De gelijkbenige driehoek in het plaatje staat ook twee keer op het werkblad.

a

Teken heel precies de omgeschreven cirkel van driehoek $A B C$ .

b

Teken in een nieuwe figuur heel precies de ingeschreven cirkel van de driehoek.

c

Leg uit dat de de top van de driehoek, het middelpunt van de omgeschreven cirkel en het middelpunt van de ingeschreven cirkel op één lijn liggen.

De punten binnen driehoek $A B C$ kun je verdelen in drie soorten: die het dichtst bij lijn $A B$ liggen, die het dichtst bij lijn $B C$ liggen en die het dichtst bij lijn $A C$ liggen.

d

Kleur de punten die het dichtst bij lijn $B C$ liggen.

De punten binnen driehoek $A B C$ kun je ook verdelen in drie andere soorten: die het dichtst bij punt $A$ liggen, die het dichtst bij punt $B$ liggen en die het dichtst bij punt $C$ liggen.

e

Kleur de punten die het dichtst bij $B$ liggen.

2

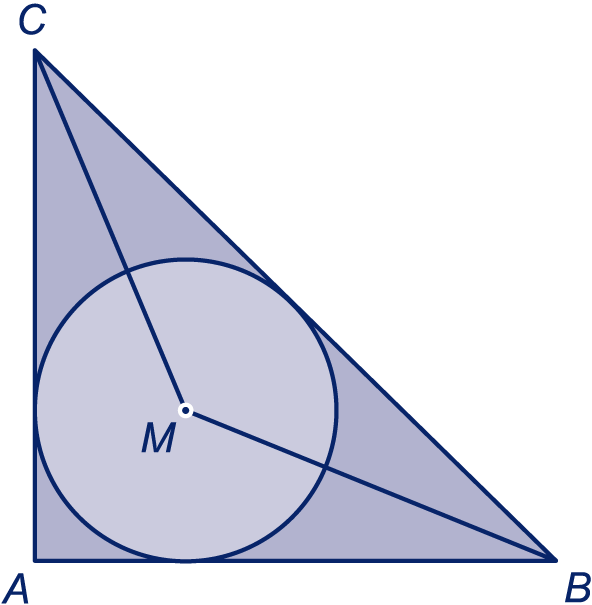
Driehoek $A B C$ is gelijkbenig en rechthoekig. $M$ is het middelpunt van de ingeschreven cirkel van driehoek $A B C$ .

Bereken de grootte van hoek $B M C$ .
Schrijf netjes op hoe je dat gevonden hebt.

3

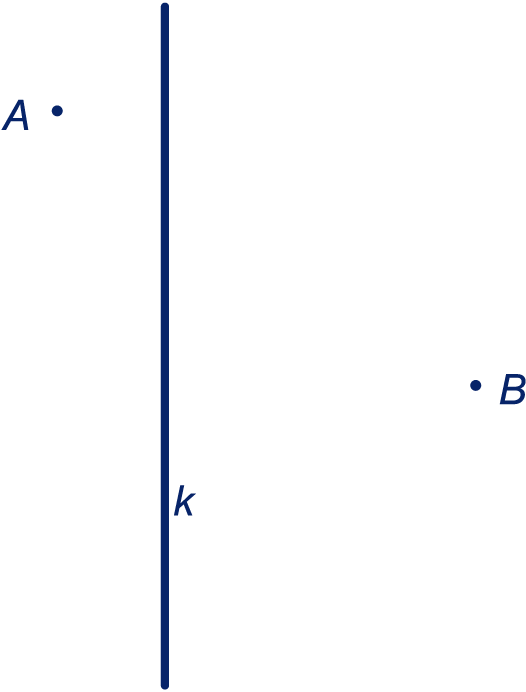
De tekening bij deze opgave staat ook op het werkblad.

Kleur het gebied waar de punten liggen met de volgende twee eigenschappen: ze liggen minder dan 1 cm van lijn $k$ én ze liggen dichter bij $A$ dan bij $B$ .

4

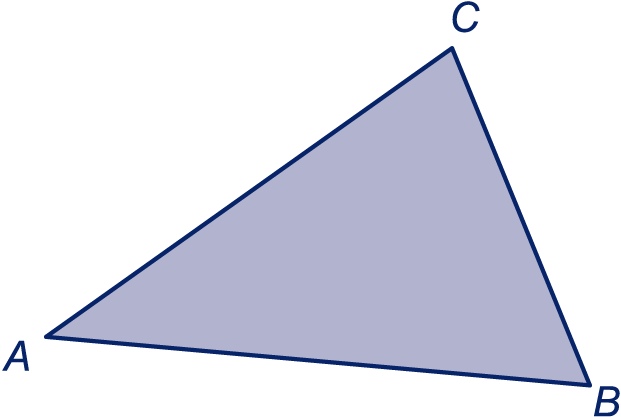
Driehoek $A B C$ staat ook op het werkblad.

Kleur de punten binnen de driehoek met de volgende twee eigenschappen: ze liggen dichter bij lijn $A C$ dan bij lijn $B C$ én ze liggen dichter bij $B$ dan bij $A$ .

5

a

Teken met je geodriehoek een gelijkbenige driehoek $A B C$ met $A C = B C = 4$ cm en $∠ B A C = 50 °$ .

b

Teken de deellijn van hoek $A$ en ook de deellijn van hoek $B$ .

c

Bereken $∠ A C B$ .

$S$ is het snijpunt van de twee deellijnen.

d

Bereken $∠ A S B$ .

e

Waarom is lijn $C S$ de deellijn van hoek $A C B$ ?

f

Bereken $∠ A S C$ .

g

Waarom is lijn $C S$ de middelloodlijn van lijnstuk $A B$ ?

6

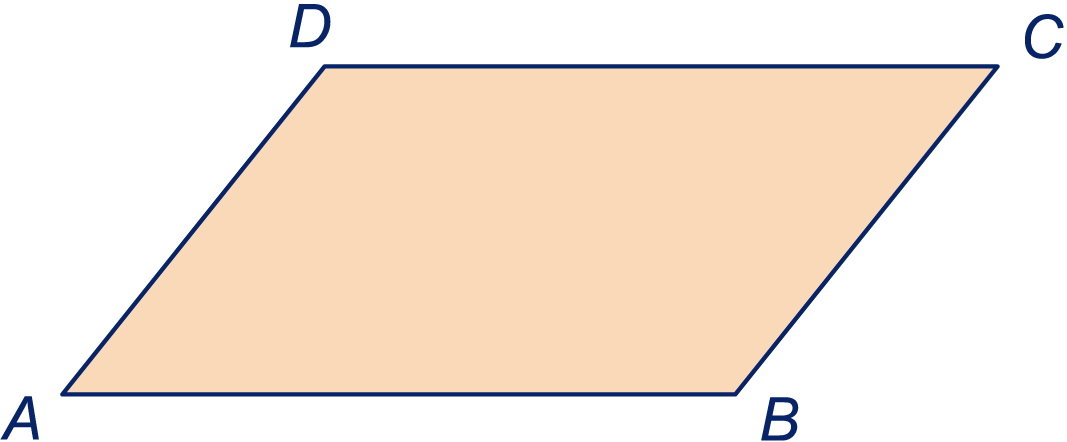
Het parallellogram in de tekening staat ook op het werkblad. In het hoofdstuk Hoeken heb je gezien dat $∠ A + ∠ D = 180 °$ .

a

Teken de deellijn van hoek $A$ en die van hoek $D$ .

Het snijpunt van de twee deellijnen noemen we $S$ .

b

Bereken $∠ S A D$ .

c

Bereken $∠ A D C$ en daarna $∠ A D S$ .

d

Hoe groot is dus hoek $A S D$ ?

Je hebt de deellijnen van de hoeken $A$ en $D$ getekend.

e

Teken ook de deellijnen van de andere twee hoeken van het parallellogram.

f

Welk soort figuur wordt door de vier deellijnen ingesloten?

7

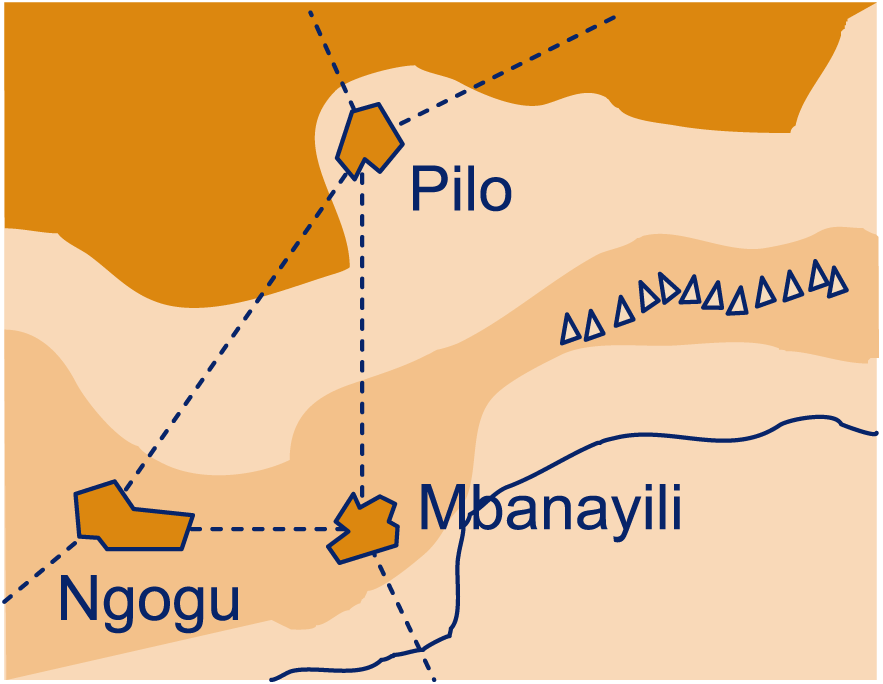
Ghana is een land in Afrika. Het grootste deel van het jaar is het noorden van Ghana erg droog. In dat gebied liggen de dorpen Pilo, Ngogu en Mbanayili. De bewoners van deze drie dorpen besluiten een waterput te graven. Die put moet even ver van elk van de drie dorpen af liggen.

Zoek deze plaats op het werkblad. Geef die plek op je kaartje aan met een rode stip. Schrijf er "put" bij.
Laat in je tekening duidelijk zien hoe je die plek gevonden hebt.

8

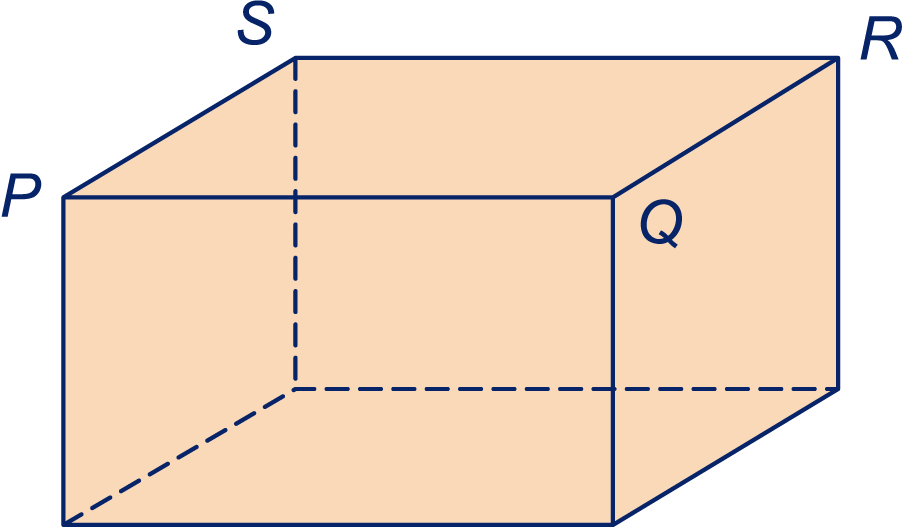
De balk staat ook op het werkblad.

$P$ , $Q$ , $R$ en $S$ zijn hoekpunten van de balk. Bekijk de middens van de twaalf ribben. Vier van die middens liggen op gelijke afstand van $P$ en $Q$ .

a

Geef deze vier middens van de ribben aan met een dikke blauwe punt.

b

Kleur nu alle punten blauw, die binnenin de balk even ver van $P$ als van $Q$ liggen.

Er is één punt in het bovenvlak, dat even ver van de vier hoekpunten $P$ , $Q$ , $P$ en $S$ ligt.

c

Kleur dit punt rood.

d

Kleur nu alle punten binnenin de balk rood, die even ver van de vier punten $P$ , $Q$ , $R$ en $S$ af liggen.

9

a

Teken een lijn met daarop een punt $C$ , zoals in het plaatje.

b

Teken, heel precies, alle mogelijke verschillende gelijkbenige driehoeken $A B C$ , waarvan een hoek $40 °$ is en een zijde 3 cm. De getekende lijn moet deellijn van de driehoek zijn.
Schrijf in elke hoek van de driehoek hoe groot hij is en geef aan welke zijde(n) 3 cm is (zijn).