21.4 Oppervlaktes van allerlei figuren >

Oppervlakte van roosterfiguren

10, 10, 5, 5, 10

F: 7∙3 – 10,5 – 3,5 = 7
G: 4∙5 – 6 – 3 – 2,5 = 8,5
H: 8∙7 – 7,5 – 10,5 – 2,5 – 7,5 – 20 = 8
I: 4∙4 – 2 – 2 – 2 – 2 = 8
J: 3∙4 – 6 – 2 = 4

De oppervlakte van een parallellogram

Alle vier de parallellogrammen hebben oppervlakte 12 hokjes.

... 12 hokjes.

$2 \cdot 3,7 = 7,4$ dm²

$5 : 2 = 2,5$ dm

Linker parallellogram: basis 2,5 cm, hoogte 3,2 cm
Rechter parallellogram: basis 3,8 cm, hoogte 2,1 cm.

De oppervlakte van het linker parallellogram is $2,5 \cdot 3,2 = 8$ cm².
De oppervlakte van het rechter parallellogram is $3,8 \cdot 2,1 = 7,98$ cm².
Dat de uitkomsten niet precies gelijk zijn, komt door meetfouten.

De hoogte die bij basis 4 cm hoort is 2,1 cm (als je het parallellogram in de juiste afmetingen tekent.) Dat geeft oppervlakte 8,4 cm².
De hoogte die bij basis 3 cm hoort is 2,8 cm. Dat geeft oppervlakte 8,4 cm²

Zie het antwoord op vraag a.

basis 3 en hoogte 3,5 (gemeten) geeft oppervlakte 10,5 cm²

basis 3 en hoogte 2 (gemeten) geeft oppervlakte 6 cm²

De oppervlakte van $A B C D$ is $10 \cdot 7,5 = 75$ m².

$B C = 75 : 6 = 12,5$ m

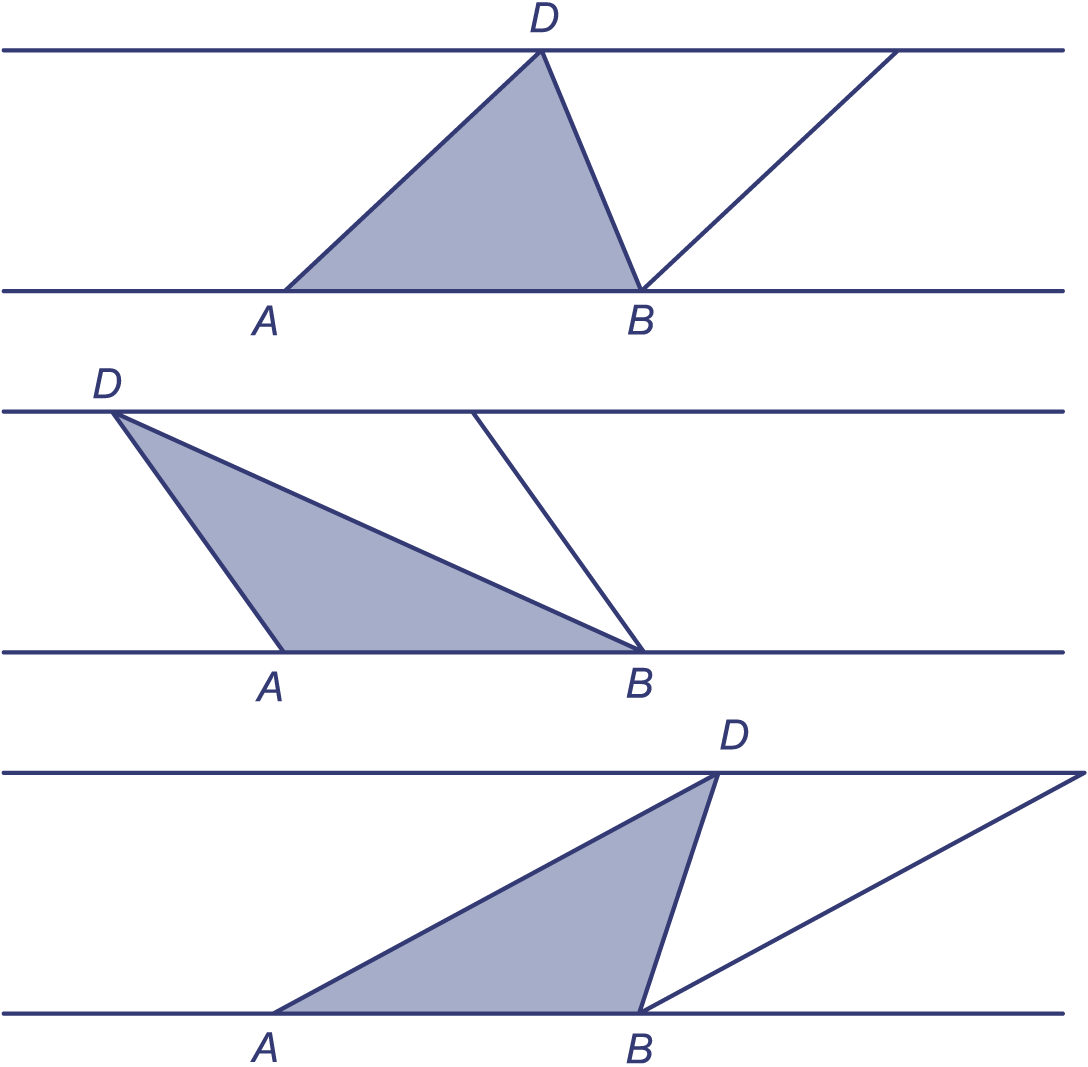
Ze hebben alledrie dezelfde oppervlakte. Dat komt omdat de figuren dezelfde basis en dezelfde hoogte hebben.
(De derde figuur moet voor dit argument in twee parallellogrammen verdeeld worden.)

Ze hebben alledrie oppervlakte 12. De derde figuur kun je verdelen in vier parallellogrammen, met oppervlakte 2, 4, 2 en 4.
De middelste figuur kun je (in gedachten) in dunne schijfjes verdelen. Dat zijn nagenoeg parallellogrammen en daarvan is de oppervlakte 2 keer de hoogte. De totale oppervlakte wordt dan 2 keer de som van al die hoogtes, dus 2 keer 6.

De oppervlakte is hoogstens 24, namelijk als de hoeken recht zijn, en kan willekeurig dicht bij 0 liggen als het parallellogram erg "plat" is (met twee hoeken van bijna $0 °$ )

De oppervlakte van een driehoek

De parallellogrammen hebben oppervlakte $41 \cdot 19 = 779$ mm², $24 \cdot 32 = 768$ mm² , $60 \cdot 13 = 780$ mm²; zeg dat de oppervlakte van de parallellogrammen ongeveer 780 mm² is.
De oppervlakte van de driehoek is dan de helft daarvan, dus (ongeveer) 390 mm².

opp. $A B C D = 3 \cdot 2 = 6$ cm²
opp. $A B D = 6 : 2 = 3$ cm²

opp. $A B C = 12 \cdot 8 : 2 = 48$

De zijde $B C$ kun je berekenen, want $B C \cdot 10 : 2 = 48$ . Dus $10 \cdot B C = 96$ , dus $B C = 9,6$ .

$B C^{2} = 15^{2} + 20^{2} = 625$ . Dus $B C = \sqrt{625} = 25$ .

opp. $A B C = 20 \cdot 15 : 2 = 150$

$B C \cdot A D : 2 = 150$
$25 \cdot A D : 2 = 150$
$25 \cdot A D = 300$
$A D = 12$

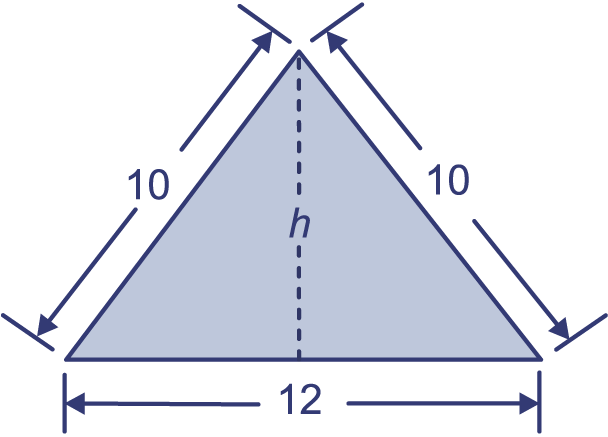
Teken de hoogtelijn en bereken de hoogte $h$ van de driehoek met de stelling van Pythagoras.

$h^{2} = 10^{2} - 6^{2} = 64$ , dus $h = \sqrt{64} = 8$ .
opp. driehoek = $12 \cdot 8 : 2 = 48$

Een hellende kant is $20$ bij $\sqrt{8^{2} + 15^{2}} = 17$
Oppervlakte voorkant: $\frac{1}{2} \cdot 16 \cdot 15 = 120$
Oppervlakte hellende kant: $17 \cdot 20 = 340$
Totaal: $2 \cdot 120 + 2 \cdot 340 = 920$ dm² $= 9,2$ m²

Inhoud $= \frac{1}{2} \cdot 15 \cdot 16 \cdot 20 = 2400$ dm³