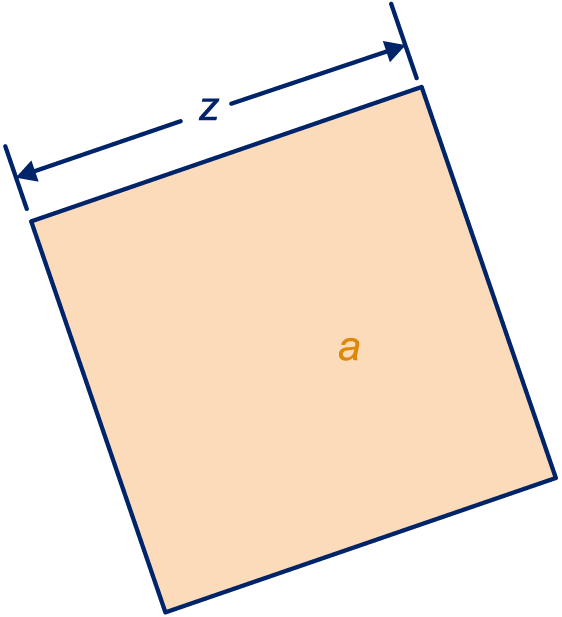
27.2 Zijde en oppervlakte van een vierkant >

Wat is een wortel?

De zijde van een vierkant noemen we $z$ (cm) en de oppervlakte $a$ ( ${cm}^{2}$ ).

Neem de tabel over en vul hem verder in.
Voorbeeld $1 \frac{1}{2} \cdot 1 \frac{1}{2} = \frac{3}{2} \cdot \frac{3}{2} = \frac{9}{4} = 2 \frac{1}{4}$

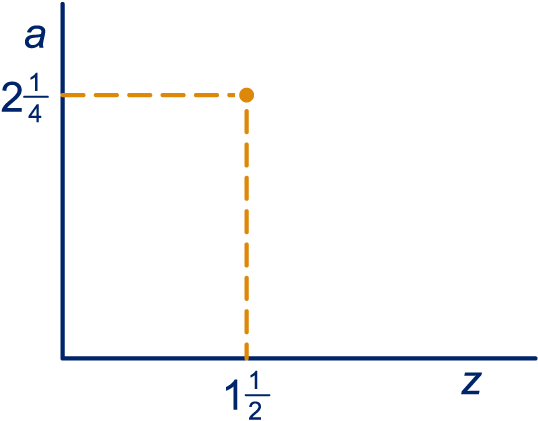
Teken op een blad mm-papier de punten bij de tabel, $z$ horizontaal ( $0 \leq z \leq 5$ ) en $a$ verticaal.
Hiernaast is dat gedaan voor $z = 1 \frac{1}{2}$ en $a = 2 \frac{1}{4}$ .
Verbind de punten met een vloeiende lijn.

Lees zo nauwkeurig mogelijk af wat $z$ is als $a = 5$ .

Bij een zijde hoort een oppervlakte en bij een oppervlakte hoort een zijde.

Als de zijde $z$ is, dan is de oppervlakte $z^{2}$ .
Als de oppervlakte $a$ is, dan is de zijde $\sqrt{a}$ .

$\sqrt{a}$ wordt ook wel de vierkantswortel van $a$ genoemd. In het Engels spreekt men van “square root” $a$ . (square=vierkant, root=wortel). Pas in de 17de eeuw heeft het teken $\sqrt{}$ algemeen ingang gevonden. Misschien is het teken afkomstig van de kleine letter $r$ (van het Latijnse woord radix, wat wortel betekent).

Met $\sqrt{2 \frac{1}{4}}$ bedoelen we de zijde van een vierkant met oppervlakte $2 \frac{1}{4}$ . Je kunt dit getal zonder $\sqrt{}$ -teken schrijven: $\sqrt{2 \frac{1}{4}} = 1 \frac{1}{2}$ .

Wat is het kwadraat van $\sqrt{\frac{1}{4}}$ , van $\sqrt{1,96}$ , van $\sqrt{7}$ , van $\sqrt{1234}$ (zonder rekenmachine)?

Als een getal eindigt op het cijfer $3$ , dan eindigt het kwadraat van dat getal op het cijfer $9$ . Kun jij dat uitleggen?

Maak een lijst voor de cijfers $0$ tot en met $9$ :
als een getal eindigt op het cijfer $\dots$ , dan eindigt het kwadraat van dat getal op het cijfer $\dots$ .

Waarom kan $98765432$ geen kwadraat zijn?

Kun je zonder je rekenmachine te gebruiken zeggen hoeveel cijfers achter de komma ${301,23}^{2}$ heeft?

Als een getal $4$ cijfers achter de komma heeft, hoeveel cijfers achter de komma heeft het kwadraat van dat getal dan? Leg dat uit.

De getallen hieronder kun je ook zonder $\sqrt{}$ -teken schrijven. Doe dat, zonder rekenmachine.

$\sqrt{1}$

$\sqrt{100}$

$\sqrt{\frac{1}{100}}$

$\sqrt{10.000}$

$\sqrt{0,01}$

$\sqrt{0,0004}$

$\sqrt{36}$

$\sqrt{0,36}$

$\sqrt{121}$

$\sqrt{1,21}$

$\sqrt{0,09}$

$\sqrt{0,49}$

$\sqrt{\frac{1}{4}}$

$\sqrt{6 \frac{1}{4}}$

$\sqrt{\frac{9}{25}}$

$\sqrt{\frac{25}{9}}$

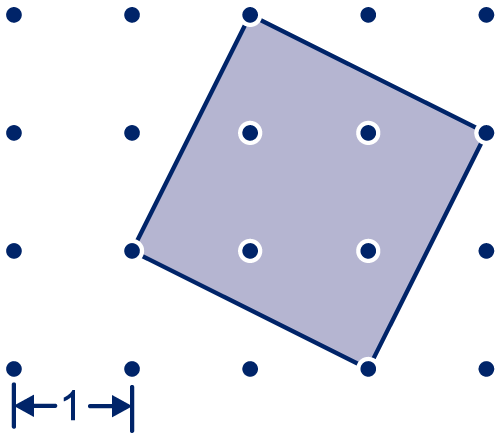
In het rooster is een vierkant getekend

Bepaal de exacte oppervlakte van het vierkant door hokjes te tellen.
Teken hiervoor het vierkant eventueel over op roosterpapier.

Meet de lengte van de zijde van het vierkant.

Kwadrateer het getal dat je in het vorige onderdeel hebt gemeten. Is het gemeten getal gelijk aan $\sqrt{5}$ ?

Het gemeten getal is een benadering van $\sqrt{5}$ . Op de rekenmachine vind je een nauwkeuriger benadering van $\sqrt{5}$ , (de meeste rekenmachines geven negen decimalen): $\sqrt{5} \approx 2,236067977$ .

$2,236067977$ is niet precies gelijk aan $\sqrt{5}$ . Leg dat uit met opgave 6.

Lees uit de grafiek van opgave 3 af wat $z$ is als $a = 20$ .
Het getal dat je afgelezen hebt, is een benadering voor $\sqrt{20}$ .

Benader het getal $\sqrt{20}$ ook ook met je rekenmachine.
Zie je een verband tussen $\sqrt{20}$ en $\sqrt{5}$ ?

Dat $\sqrt{20}$ en $2 \cdot \sqrt{5}$ ongeveer hetzelfde zijn kun je in de grafiek en met het rekenmachine wel zien, maar dat $\sqrt{20}$ en $2 \cdot \sqrt{5}$ exact hetzelfde zijn, kun je met een berekening concluderen door beide getallen te kwadrateren.
${(2 \cdot \sqrt{5})}^{2} = 2 \cdot \sqrt{5} \cdot 2 \cdot \sqrt{5} = 2 \cdot 2 \cdot \sqrt{5} \cdot \sqrt{5} = 2 \cdot 2 \cdot 5 = 20$ en ${(\sqrt{20})}^{2} = 20$ .

Laat zo ook zien dat
$3 \cdot \sqrt{6} = \sqrt{54}$ ; $5 \cdot \sqrt{6} = \sqrt{150}$ ; $4 \cdot \sqrt{5} = \sqrt{80}$ .

In het vervolg schrijven we $3 \sqrt{6}$ in plaats van $3 \cdot \sqrt{6}$ .

Neem over en vul in plaats van het vraagteken het passende getal in.
Voorbeeld
$3 \sqrt{6} = \sqrt{54}$

$3 \sqrt{5} = \sqrt{?}$	$\frac{1}{2} \sqrt{20} = \sqrt{?}$
$2 \sqrt{7} = \sqrt{?}$	$0,1 \sqrt{200} = \sqrt{?}$

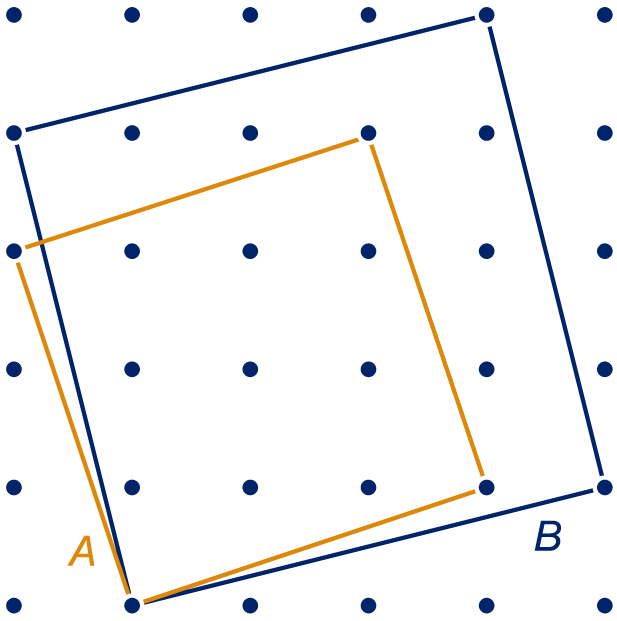
Getekend zijn twee vierkanten, $A$ en $B$ .

Bepaal door hokjes te tellen de oppervlakte van $A$ .

Teken $A$ over op roosterpapier en benader $\sqrt{10}$ door de zijde van $A$ te meten, in één decimaal nauwkeurig.

Tom heeft $3,2$ cm gemeten als zijde van vierkant $A$ .
Hij berekent ${3,2}^{2} = 10,24$ .

Is $3,2$ groter of kleiner dan $\sqrt{10}$ ?

Hoe groot is de oppervlakte van vierkant $B$ ?

Benader door meten de wortel uit de oppervlakte van $B$ .

Ga door rekenen na of je antwoord te groot of te klein is.

Neem over en vul het juiste teken in: <, > of =. Controleer je antwoord door te kwadrateren. De eerste is al als voorbeeld gedaan.

$\sqrt{3}$	>	$1,7$	want ${1,7}^{2} = 2,89 < 3$
$\sqrt{17}$	__	$4,1$	want _____________
$\sqrt{33}$	__	$5,8$	want _____________
$\sqrt{56,2}$	__	$7,5$	want _____________
$\sqrt{6,25}$	__	$2,5$	want _____________

Getekend is een vierkant. De hoekpunten zijn roosterpunten.
Jim heeft de oppervlakte berekend en vond $12,96$ .

Hoe heeft hij dat antwoord gevonden?

Wat vind jij daarvan?

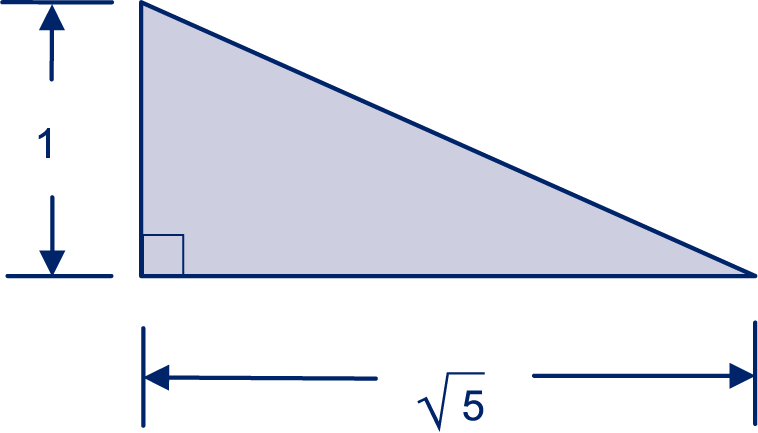
Van een rechthoekige driehoek zijn de rechthoekszijden $1$ en $\sqrt{5}$ .

Hoe lang is de schuine zijde? Geef het exacte antwoord, laat zo nodig een $\sqrt{}$ -teken in je antwoord staan.

Afstanden in een rooster

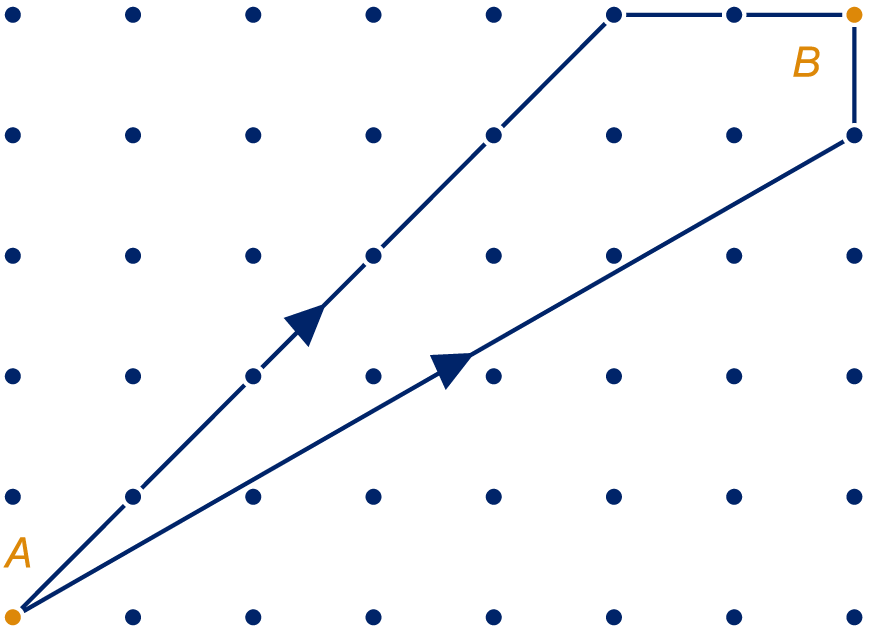
We werken in een rooster van $1$ bij $1$ cm. Daarin zijn twee routes getekend van $A$ naar $B$ . De tekening bij de opgave staat op het werkblad op ware grootte. Als je de routes meet, blijken ze ongeveer even lang te zijn.

Kun jij met je rekenmachine berekenen welke van de twee de langste is?

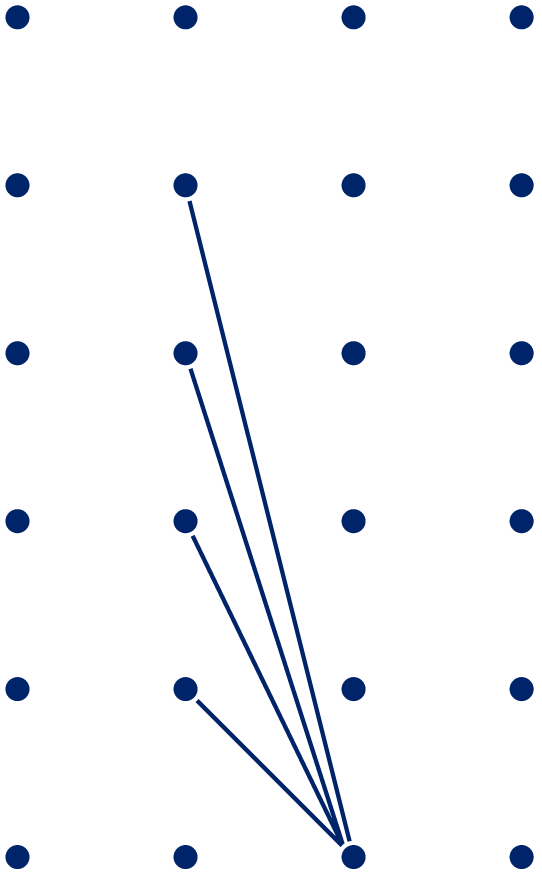
In het rooster van $1$ bij $1$ cm zijn vier lijnstukken getekend.

Schrijf op hoe lang ze zijn. Geef een exact antwoord, gebruik zo nodig een $\sqrt{}$ -teken en geef een benadering in één decimaal nauwkeurig.

Teken op roosterpapier lijnstukken met de volgende lengtes: $\sqrt{18}$ , $\sqrt{20}$ , $\sqrt{26}$ en $\sqrt{32}$ .

13s

15s

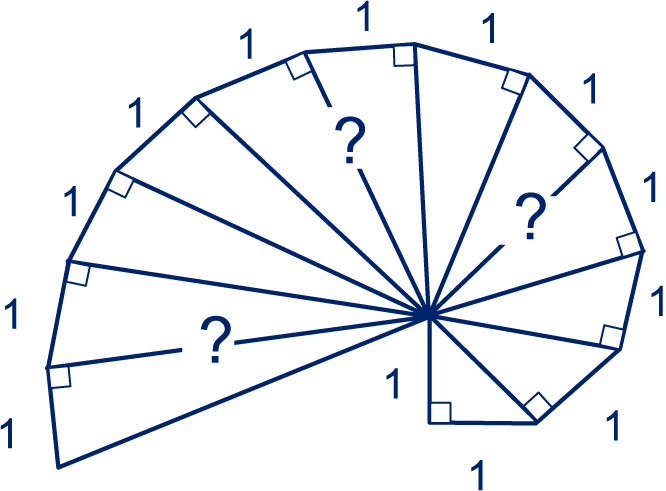
Het “slakkenhuis” bestaat uit op elkaar aansluitende rechthoekige driehoeken, waarvan een rechthoekszijde lengte $1$ heeft. De kleinste driehoek heeft twee rechthoekszijden $1$ .
Bij drie lijnstukken staat een vraagteken.

Hoe lang zijn die lijnstukken?
Geef exacte antwoorden , gebruik zo nodig een $\sqrt{}$ -teken.

In de tweede figuur is het slakkenhuis voortgezet.

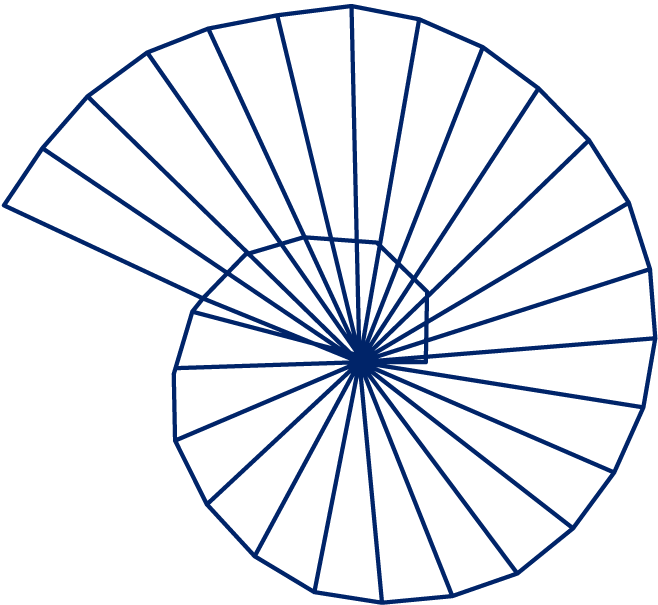
Zijn de hoeken om het centrum alle even groot?
Licht je antwoord toe.

Het eerste lijnstuk heeft lengte $1$ , het tweede $\sqrt{2}$ .
Het hoeveelste lijnstuk is heeft lengte $1000$ ?

Zijden en oppervlakte van rechthoeken

Een wedstrijdbiljart heeft een oppervlakte van $4 m^{2}$ . Het laken is twee keer zo lang als breed.

Bereken de afmetingen van het biljartlaken in mm nauwkeurig. Gebruik je rekenmachine.

Een rechthoek heeft oppervlakte $15 m^{2}$ . De rechthoek is $3$ keer zo lang als breed.

Bereken de afmetingen van de rechthoek in mm nauwkeurig. Gebruik je rekenmachine.

16s

18s

We gaan rechthoeken in de breedte dubbelvouwen (we halveren dus de langste zijde). Meestal is de halve rechthoek niet gelijkvormig met de oorspronkelijke rechthoek. Dat kan hij wel zijn! We starten met een rechthoek van $2$ bij $3$ . De lange zijde is $1 \frac{1}{2}$ keer zo lang als de korte zijde.
De halve rechthoek meet $1 \frac{1}{2}$ bij $2$ . De lange zijde is $1 \frac{1}{3}$ keer zo lang als de korte zijde.

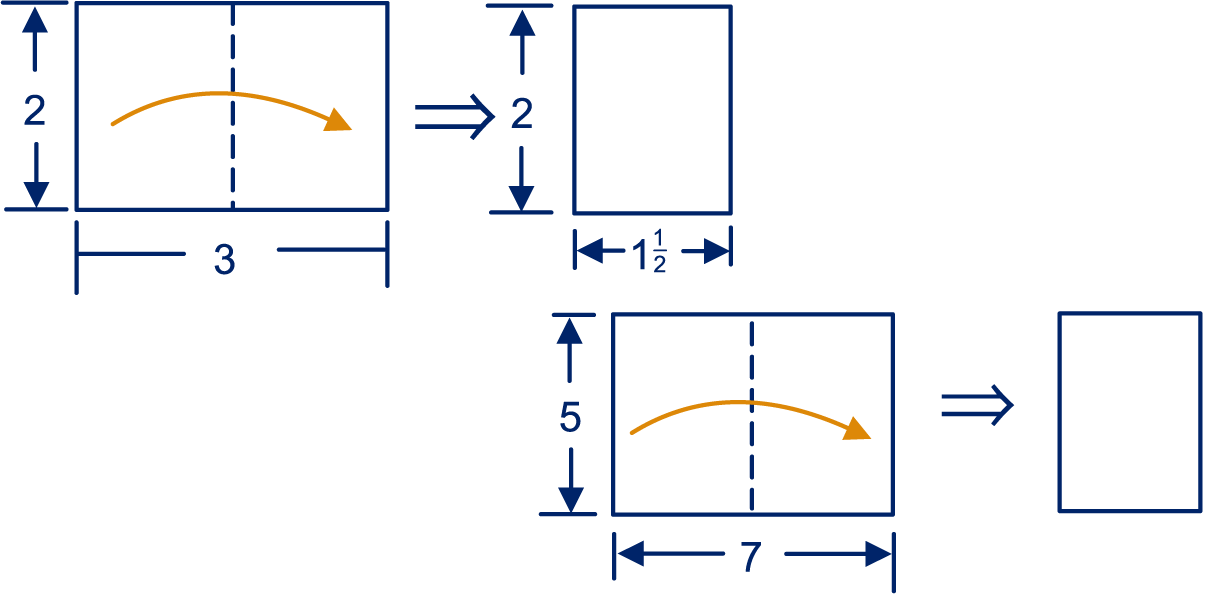
Is de halve rechthoek gelijkvormig met de oorspronkelijke rechthoek?
Zelfde vraag bij een rechthoek van $5$ bij $7$ .

En bij een rechthoek van $12$ bij $17$ .

De rechthoek van $12$ bij $17$ is wel bijna gelijkvormig met zijn eigen helft; het scheelt niet zo veel.
Er is een rechthoek die precies gelijkvormig is zijn eigen helft. Zeg dat die rechthoek lengte $2$ heeft en breedte $x$ .

Bereken $x$ exact.

Opmerking
De blaadjes waarop jouw zelftoetsen en proefwerken staan gedrukt, zijn van die verhouding: als je ze dubbelvouwt krijg je een rechthoek die gelijkvormig is met het uitgevouwen vel. Diezelfde verhouding tref je aan bij een krantenpagina, bij briefkaarten, enzovoort.