27.2 Zijde en oppervlakte van een vierkant >

Wat is een wortel?

Langzamer.

Nee. Hij doet alsof de oppervlakte gelijkmatig toeneemt. Je moet als zijde $\sqrt{12}$ nemen.

Noem de zijde van het oorspronkelijke vierkant $x$ dan is de toename van de oppervlakte $2 x + 1 = 1001$ , dus $x = 500$ .
De oppervlakte was $500^{2} = 250.000$ .

$1$

$10$

$\frac{1}{10}$

$100$

$0,1$

$0,02$

$6$

$0,6$

$11$

$1,1$

$0,3$

$0,7$

$\frac{1}{2}$

$2 \frac{1}{2}$

$\frac{3}{5}$

$1 \frac{2}{3}$

$\frac{1}{4}$ ; $1,96$ ; $7$ ; $1234$

$(\dots 0 + 3) \cdot (\dots 0 + 3) = \dots 0 \cdot \dots 0 + 2 \cdot 3 \cdot \dots 0 + 9$ en dit eindigt op een $9$ .

Getal eindigt op...	Kwadraat van dat getal eindigt op...
$1$	$1$
$2$	$4$
$3$	$9$
$4$	$6$
$5$	$5$
$6$	$6$
$7$	$9$
$8$	$4$
$9$	$1$
$0$	$0$

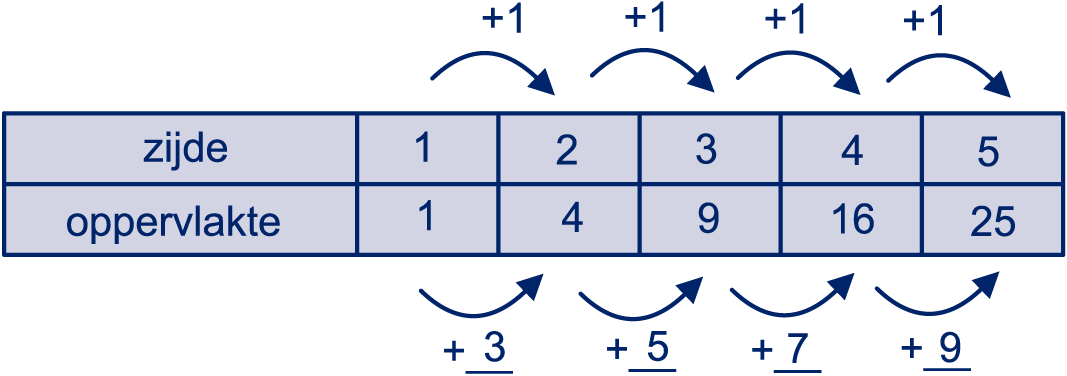
Uit het vorige onderdeel blijkt dat geen enkel kwadraat op het cijfer $2$ eindigt.

$4$

$8$ ; je vermenigvuldigt dan tienduizendsten met tienduizendsten. Je krijgt dan honderdmiljoensten die je niet kunt vereenvoudigen (ga dat na).

Het aantal decimalen is twee keer zo groot.

$5$

$2,2$ ongeveer

${2,2}^{2} = 4,84$ , nee

Als je dat getal kwadrateert, krijg je een getal met $18$ cijfers achter de komma, dus niet het getal $5$ .

$2, 3^{2} = 5, 29$ , dus $2,3$ is groter dan $\sqrt{5}$ .

$\sqrt{3}$	>	$1,7$	want ${1,7}^{2} = 2,89 < 3$
$\sqrt{17}$	>	$4,1$	want ${4,1}^{2} = 16,81 < 17$
$\sqrt{33}$	<	$5,8$	want ${5,8}^{2} = 33,64 > 33$
$\sqrt{56,2}$	<	$7,5$	want ${7,5}^{2} = 56,25 > 56,2$
$\sqrt{6,25}$	$=$	$2,5$	want ${2,5}^{2} = 6,25$

Hij heeft de zijde gemeten en die lengte gekwadrateerd: ${3,6}^{2} = 12,96$ .

Als het vierkant roosterpunten als hoekpunten heeft, is dat fout, want dan zie je met hokjes tellen dat de oppervlakte $13$ is.

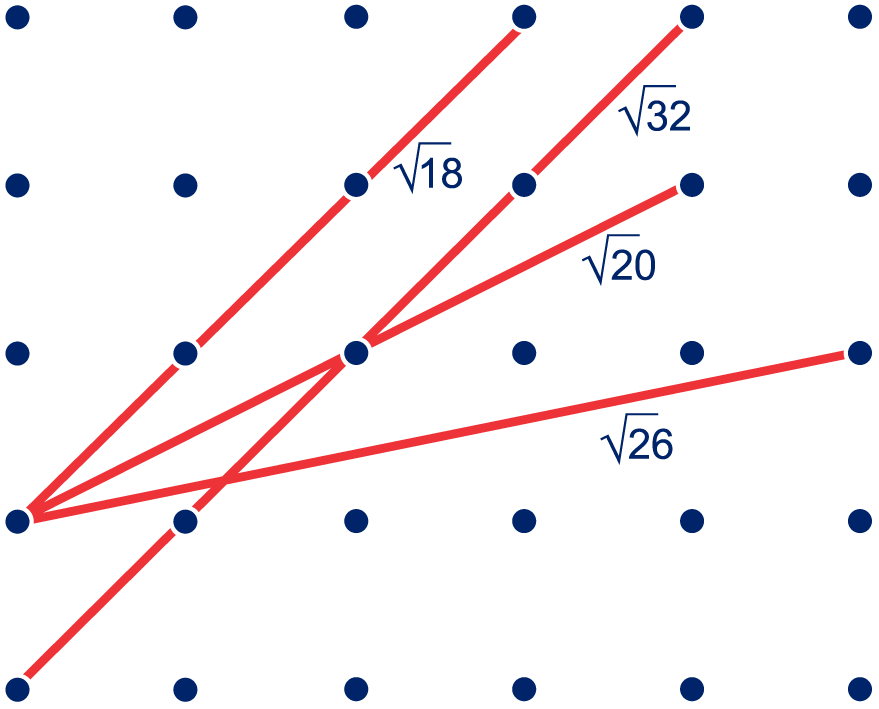
Lengte schuine zijde is $\sqrt{{\sqrt{5}}^{2} + 1^{2}} = \sqrt{6}$ .

Afstanden in een rooster

Bovenlangs: $\sqrt{5^{2} + 5^{2}} + 2 = \sqrt{50} + 2 \approx 9,07$
Onderlangs: $\sqrt{7^{2} + 4^{2}} + 1 = \sqrt{65} + 1 \approx 9,06$
Dus bovenlangs is langer.

$\sqrt{1^{2} + 1^{2}} = \sqrt{2} \approx 1,4$ ; $\sqrt{1^{2} + 2^{2}} = \sqrt{5} \approx 2,2$ ; $\sqrt{1^{2} + 3^{2}} = \sqrt{10} \approx 3,2$ ; $\sqrt{1^{2} + 4^{2}} = \sqrt{17} \approx 4,1$

13s

15s

$\sqrt{5}$ ; $\sqrt{8} = 2 \sqrt{2}$ ; $\sqrt{12} = 2 \sqrt{3}$

Nee, de overstaande rechthoekszijde is steeds $1$ en de schuine zijde wordt langer.

$1000^{2} = 1 000 000$

Zijden en oppervlakte van rechthoeken

Het wedstrijdbiljart bestaat dus uit twee vierkanten ‘tegen elkaar’ aangelegd. Eén zo’n vierkant heeft dan oppervlakte $2$ m², dus dat vierkant is $\sqrt{2}$ bij $\sqrt{2}$ m.
Het laken is dus $1414$ bij $2828$ mm.

De rechthoek bestaat uit drie vierkanten ‘tegen elkaar’ aangelegd. Eén zo’n vierkant heeft dan oppervlakte $5$ m², dus dat vierkant is $\sqrt{5}$ bij $\sqrt{5}$ m.
De rechthoek is dus $\sqrt{5}$ bij $3 \sqrt{5}$ m, dat is $2236$ bij $6708$ mm.

$‐ 2$ en $2$

$‐ \sqrt{10}$ en $\sqrt{10}$

16s

19s

Nee, want $\frac{3}{2} \neq \frac{2}{1 \frac{1}{2}} = \frac{4}{3}$ .
Nee, want $\frac{7}{5} \neq \frac{5}{3 \frac{1}{2}} = \frac{10}{7}$ .

Nee, want $\frac{17}{12} \neq \frac{12}{8 \frac{1}{2}} = \frac{24}{17}$ .

$\frac{x}{2} = \frac{1}{x} \Leftrightarrow x^{2} = 2$ , dus $x = \sqrt{2}$ , want $x > 0$ .

$2 x^{2} = 4$ $x^{2} = 2$ $x = \sqrt{2}$ of $x = ‐ \sqrt{2}$	$3 x^{2} = 15$ $x^{2} = 5$ $x = \sqrt{5}$ of $x = ‐ \sqrt{5}$
${(2 x)}^{2} = 40$ $4 x^{2} = 40$ $x^{2} = 10$ $x = \sqrt{10}$ of $x = ‐ \sqrt{10}$ ( $x = \frac{1}{2} \sqrt{40}$ of $x = ‐ \frac{1}{2} \sqrt{40}$ )	${(\frac{1}{2} x)}^{2} = 40$ $\frac{1}{4} x^{2} = 40$ $x^{2} = 160$ $x = \sqrt{160}$ of $x = ‐ \sqrt{160}$ ( $x = 2 \sqrt{40}$ of $x = ‐ 2 \sqrt{40}$ )