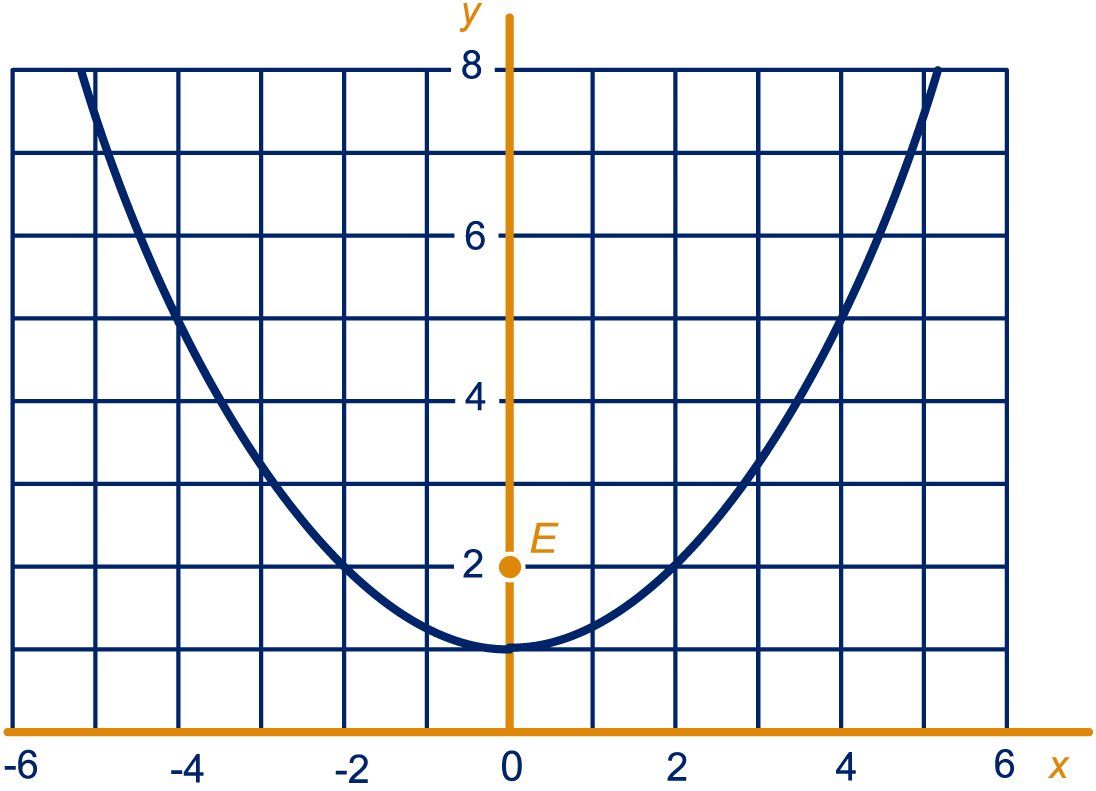
Als het goed is, heb je in de Intro dit plaatje gekregen. De punten op de parabool liggen even ver van $E$ als van de $x$ -as.
We proberen de coördinaten van punten op de parabool te berekenen. Je kunt zo zien dat het punt $(2,2)$ op de parabool ligt, want de afstand tot $E$ en de afstand tot de $x$ -as zijn beide 2.

Het punt $(4,5)$ lijkt op de parabool te liggen.

Wat is de afstand van $(4,5)$ tot de $x$ -as?
Bereken de afstand van $(4,5)$ tot $E$ . (Dat kan met de stelling van Pythagoras.)

Dus $(4,5)$ ligt inderdaad op de parabool.

Neem nu een willekeurig punt $P (x, y)$ .

Wat is de afstand van $P$ tot de $x$ -as uitgedrukt in $y$ ?
Wat is de afstand van $P$ tot $E$ uitgedrukt in $x$ en $y$ ?

Dus als $P (x, y)$ even ver van de $x$ -as als van $E$ ligt, geldt: $y^{2} = x^{2} + {(y - 2)}^{2}$ .

Werk in deze vergelijking de haakjes weg en vereenvoudig zo veel mogelijk. Schrijf je antwoord als $y$ = ....

Als je het goed gedaan hebt, heb je de vergelijking $y = \frac{1}{4} x^{2} + 1$ gevonden. Je kunt met deze vergelijking controleren dat bijv. $(4,5)$ op de parabool ligt.

Bereken de eerste coördinaat van de punten die op afstand 3, 4 en 6 van $E$ afliggen. Doe dat in twee decimalen nauwkeurig. Gebruik de vergelijking.

Het eiland is nu $E (0, \frac{1}{4})$ en de kust is de lijn $k$ met vergelijking $y = ‐ \frac{1}{4}$ .

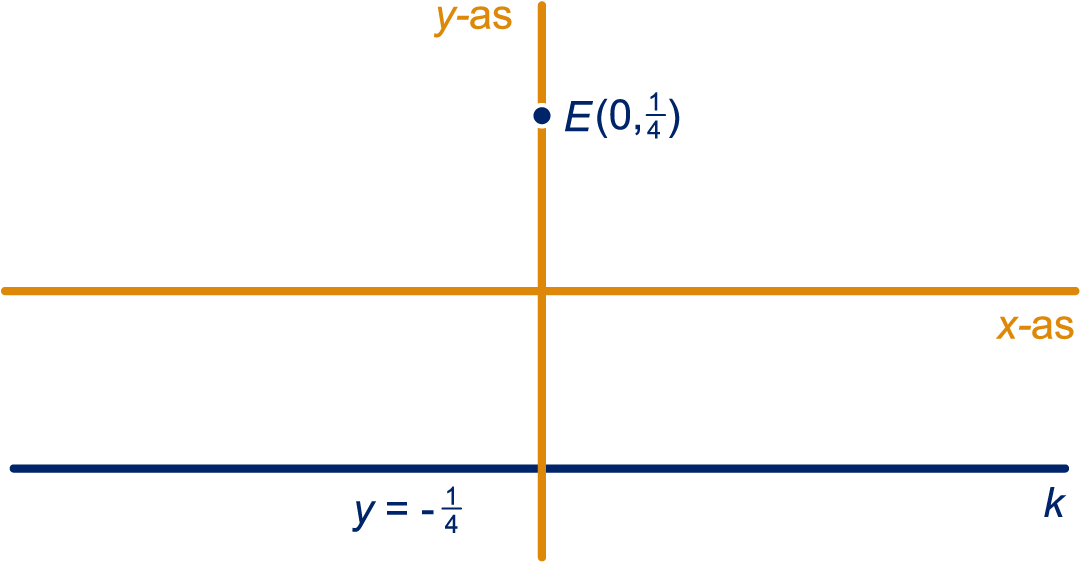
We zoeken weer een vergelijking voor de punten die even ver van $E$ als van $k$ liggen.

Bepaal van elk van de punten $P (1 \frac{1}{2},2)$ , $Q (‐3,9)$ en $R (8,64)$ zowel de afstand tot $E$ als de afstand tot lijn $k$ . Geef exacte antwoorden.

Toon aan: $(x, y)$ ligt even ver van $k$ als van $E$ , als geldt: ${(y + \frac{1}{4})}^{2} = x^{2} + {(y - \frac{1}{4})}^{2}$ .

Werk de haakjes in de vergelijking weg en schrijf de vergelijking zo eenvoudig mogelijk.

In een geschikt gekozen assenstelsel (met een geschikte eenheid) is de gebogen lijn de parabool met vergelijking $y = x^{2}$ . Deze parabool noemen we de standaardparabool.

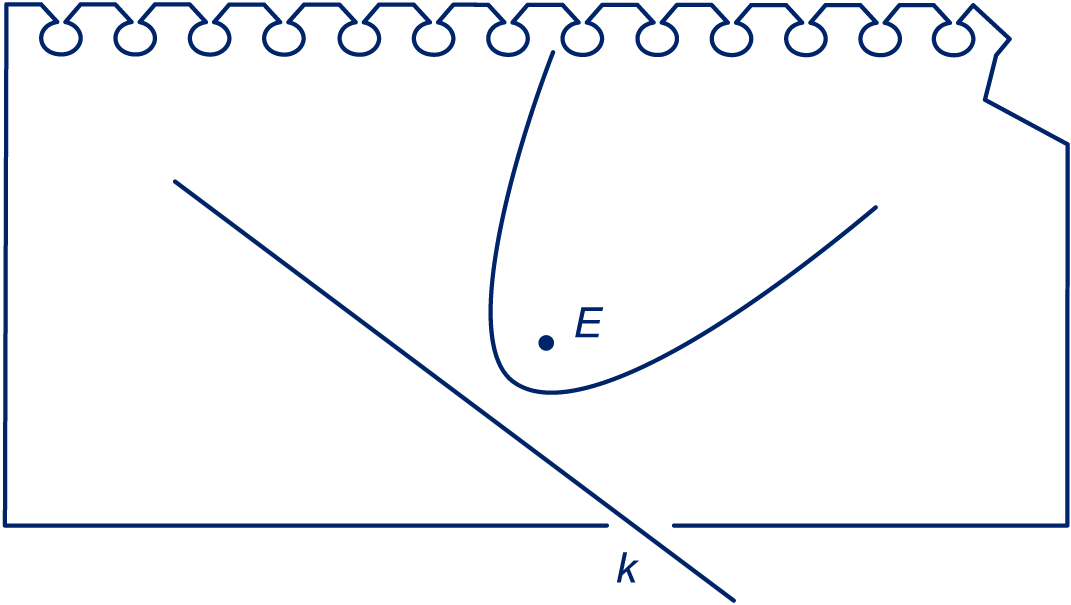
Gegeven een punt $E$ en een lijn $k$ .
De punten die even ver van $k$ als $E$ af liggen vormen een parabool.
$k$ heet de richtlijn en $E$ heet het brandpunt van de parabool.