Schoolbord, tv-scherm, A4-papier, deur, foto.

Bol, cilinder, piramide.

-

-

-

Groot Brittannië: $15:30=1:2$; Duitsland: $18:30=3:5$;
Nederland: $20:30=2:3$; Zwitserland: $30:30=1:1$

Groot Brittannië: $15:30=30:60$; Duitsland: $18:30=30:50$;
Nederland: $20:30=30:45$; Zwitserland: $30:30=30:30$

Baan Duitse vlag: $6:30=1:5$
Baan Nederlandse vlag: $\frac{20}{3}:30=20:90=2:9$

Eerste mogelijkheid: $22:33=x:18$ $\to$ $2:3=x:18$ $\to$ $x=12$
Tweede mogelijkheid: $22:33=18:x$ $\to$ $2:3=18:x$ $\to$ $x=27$

Eerste mogelijkheid: $22:33=x:a$ $\to$ $2:3=x:a$ $\to$ $\frac{2}{3}=\frac{x}{a}$ $\to$ $x=\frac{2}{3}a$
Tweede mogelijkheid: $22:33=a:x$ $\to$ $2:3=a:x$ $\to$ $\frac{2}{3}=\frac{a}{x}$ $\to$ $2x=3a$ $\to$ $x=\frac{3}{2}a=1\frac{1}{2}a$

factor $=\frac{12}{16}=\frac{3}{4}$

breedte $=\frac{3}{4}\times 12=9$ cm

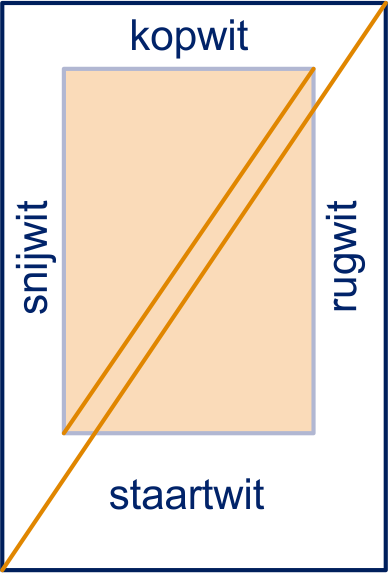
De diagonalen lopen evenwijdig. Het bedrukte deel is gelijkvormig met de hele bladzijde.

Zie voorbeeld hieronder: $5:8\ne 3:6$

De breedte van de zetspiegel wordt $20-9=11$ cm. Als de zetspiegel gelijkvormig moet zijn met de pagina zelf geldt voor de hoogte $h$ van de zetspiegel: $20:11=30:h$, dus $h=\frac{30\cdot 11}{20}=\mathrm{16,5}$ cm.
Er blijft voor het kop- en staartwit samen $30-\mathrm{16,5}=\mathrm{13,5}$ cm over.

Teken bijvoorbeeld een rechthoek van 10 bij 16 cm.

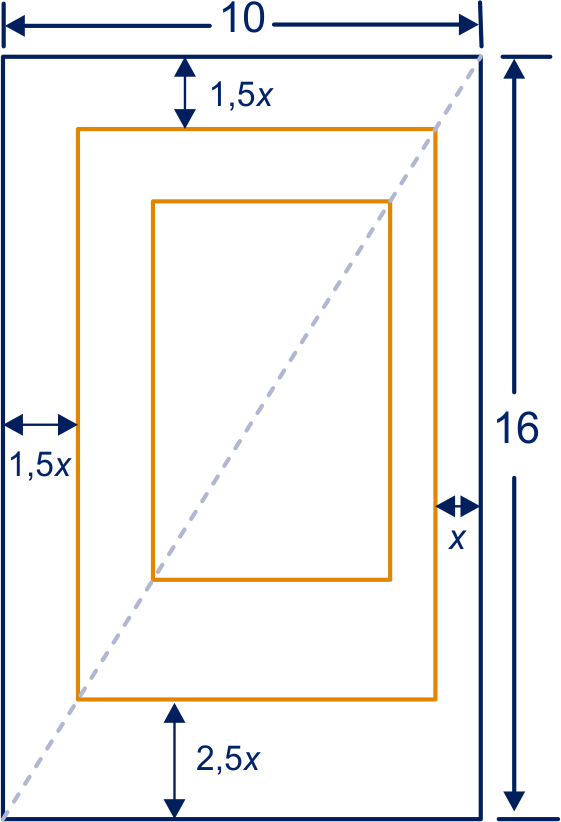
snijwit = $\mathrm{1,5}x$;
kopwit = $\mathrm{1,5}x$;
staartwit = $\mathrm{2,5}x$;
Bij een rechthoek van $10$ bij $16$ cm geldt dan:
breedte = $10-x-\mathrm{1,5}x=10-\mathrm{2,5}x$;
hoogte = $16-\mathrm{1,5}x-\mathrm{2,5}x=16-4x$

$\frac{\text{hoogte}}{\text{breedte}}=\frac{16-4x}{10-\mathrm{2,5}x}=\frac{4(4-x)}{\mathrm{2,5}(4-x)}=\frac{4}{\mathrm{2,5}}=\frac{8}{5}$, dus $\text{hoogte}:\text{breedte}=8:5$ en dus is de zetspiegel gelijkvormig met de hele pagina.

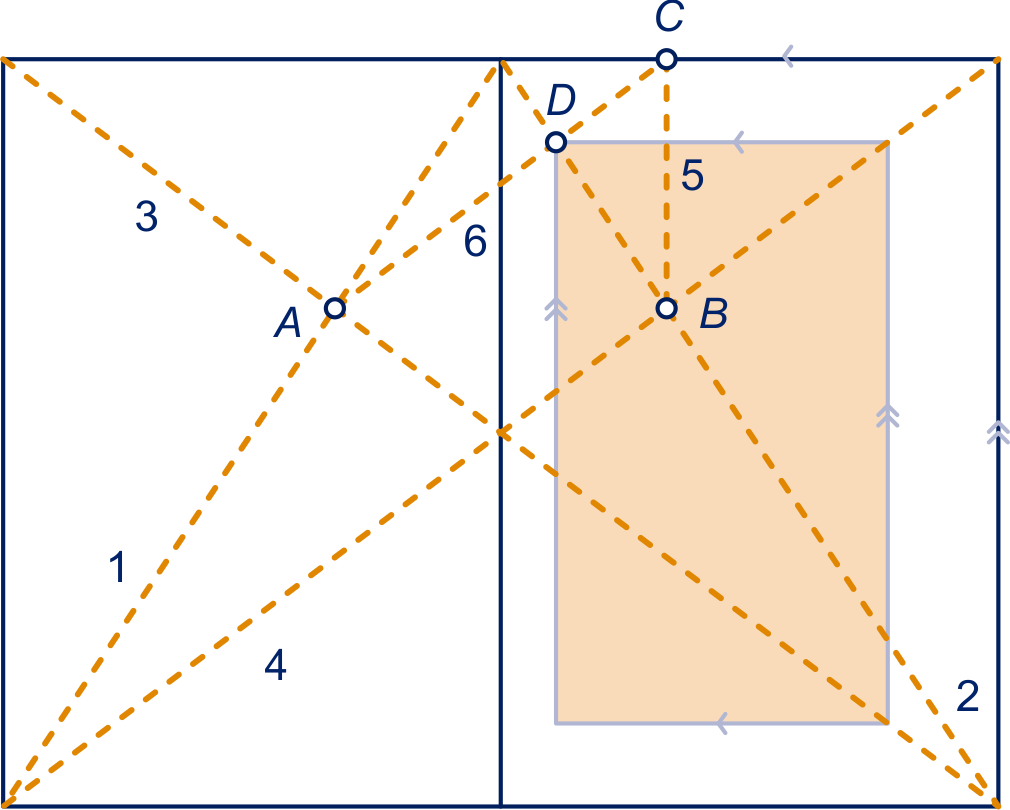
Trek eerst de twee pagina-diagonalen (1 en 2). Dan de twee spread-diagonalen (3 en 4). Dit geeft de punten A en B. Dan vanuit punt B loodrecht naar de bovenzijde geeft punt C (5). Lijnstuk AC (6) snijden met een paginadiagonaal geeft punt D. Dan met lijnstukken evenwijdig aan de paginazijdes de bladspiegel aftekenen.

Via het tellen van de hokjes wordt het $\frac{21}{\mathrm{40,5}}=\frac{14}{27}$ deel bedrukt, ofwel ongeveer $52\text{\%}$

rugwit : snijwit = 1 : 2;
kopwit : staartwit = 1 : 2

Zie linker figuur hieronder: de hoekpunten liggen op één lijn.
(Of: de diagonalen liggen op elkaar.)

Zie tweede figuur hieronder. Je ziet vier gelijkvormige rechthoeken.

Zie derde figuur hieronder.

Zie derde figuur hieronder.
De rechthoeken $ABCD$ en $AGFE$ zijn gelijkvormig. De hoeken met de stippen zijn even groot. Een stip en sterretje maken samen een hoek van $90°$. Dus in driehoek $AGS$ is hoek $S$ = $180°$ – (stip + sterretje) $=180°-90°=90°$.

Zie vierde figuur hieronder.
Draai rechthoek $EFGC$ om punt $C$ over $90°$ tegen de wijzers van de klok in. Diagonaal $CF$ draait ook $90°$ en komt in het verlengde van diagonaal $AC$ te liggen. De rechthoeken $ABCD$ en $CEFG$ zijn dan gelijkvormig.

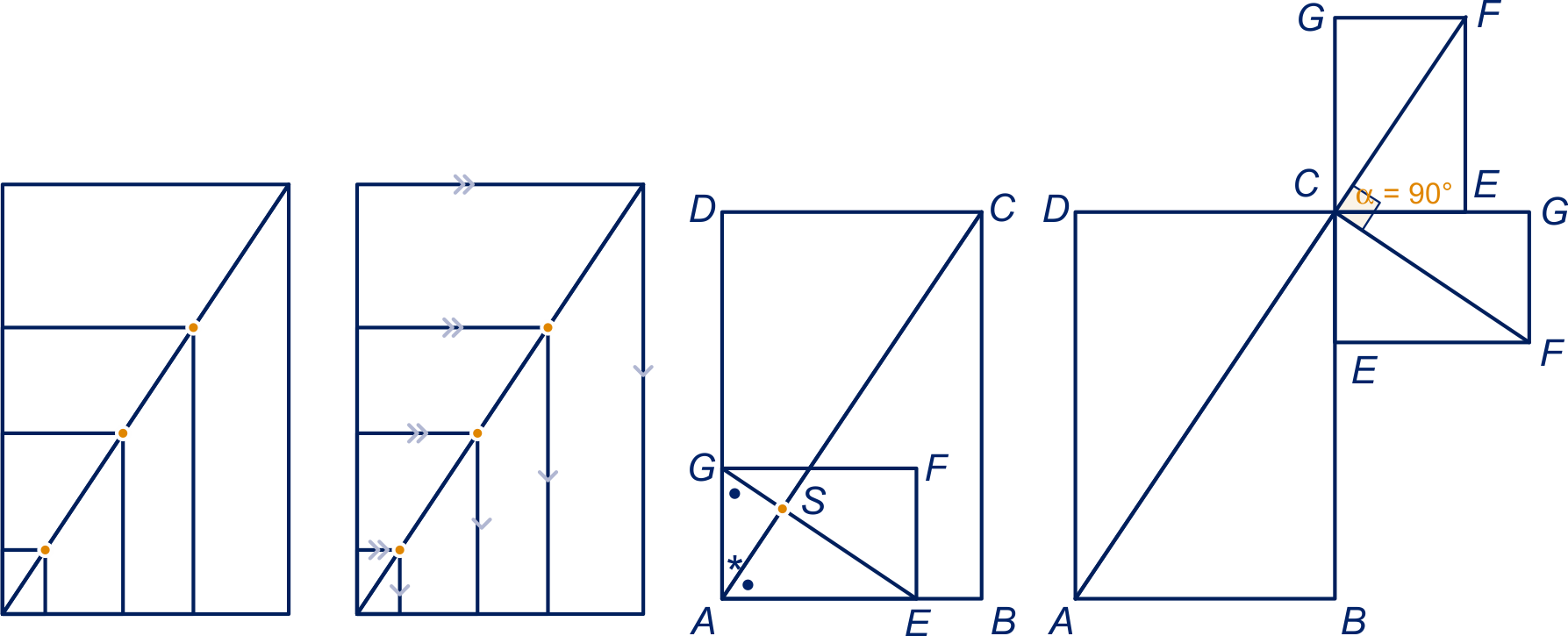
Omdat de rechthoeken gelijkvormig zijn, zijn ook de rechthoekige driehoeken gelijkvormig. Ze hebben dus dezelfde hoeken. Als de ene scherpe hoek van de driehoek $\text{α}$ is, dan is de andere hoek $\text{90}°-\text{α}$; in zo'n punt waar de diagonalen bij elkaar komen, komen deze twee hoeken samen en dus is de hoek tussen de diagonalen $\text{α}+(90°-\text{α})=90°$.

-

factor = $\mathrm{0,72}$

$v=\mathrm{1,5}$ invullen in de formule geeft $f=\mathrm{0,721}$.

Zie afmetingen in figuur hieronder.
Voor $R_0,R_2,R_4$ geldt $\text{breedte}:\text{lengte}=15:20=\mathrm{7,5}:10=\mathrm{3,75}:5=3:4$, dus ze zijn gelijkvormig.
Voor $R_1,R_3,R_5$ geldt $\text{breedte}:\text{lengte}=10:15=5:\mathrm{7,5}=\mathrm{2,5}:\mathrm{3,75}=2:3$, dus ze zijn gelijkvormig.

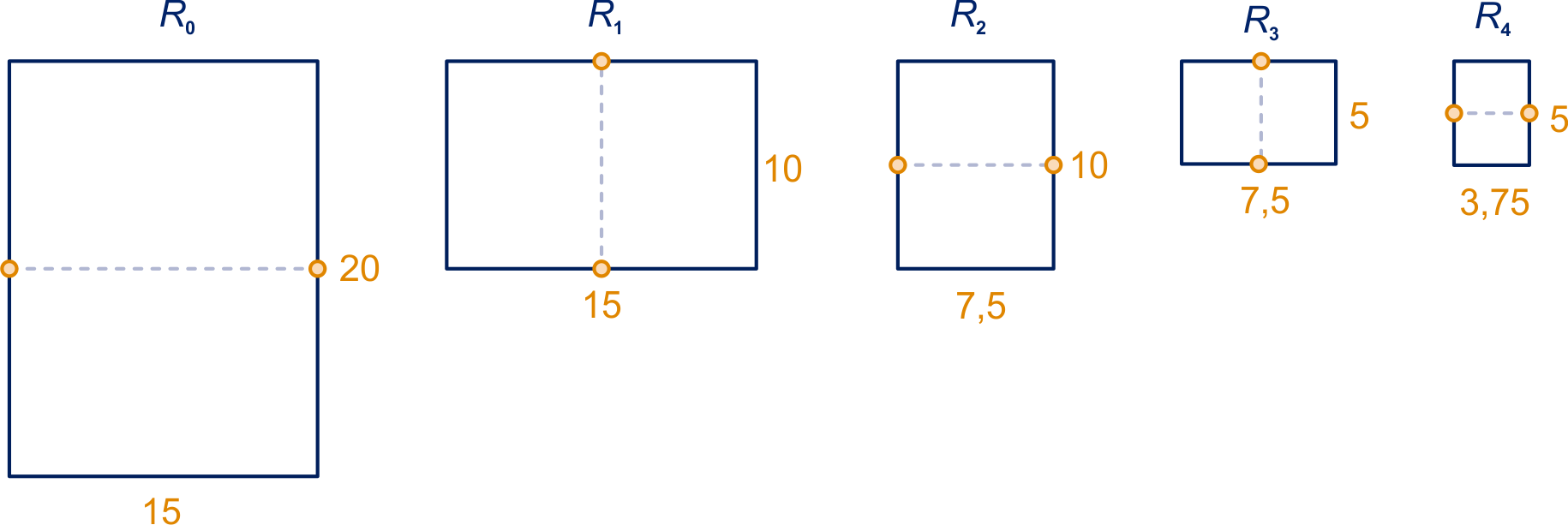
Zie figuur hieronder.
$R_0,R_2,R_4\mathrm{,...}$ blijven vierkanten, dus zijn gelijkvormig.
De verhouding van de zijden van $R_1,R_3,R_5\mathrm{,...}$ is steeds $1:2$, dus ze zijn gelijkvormig.

-

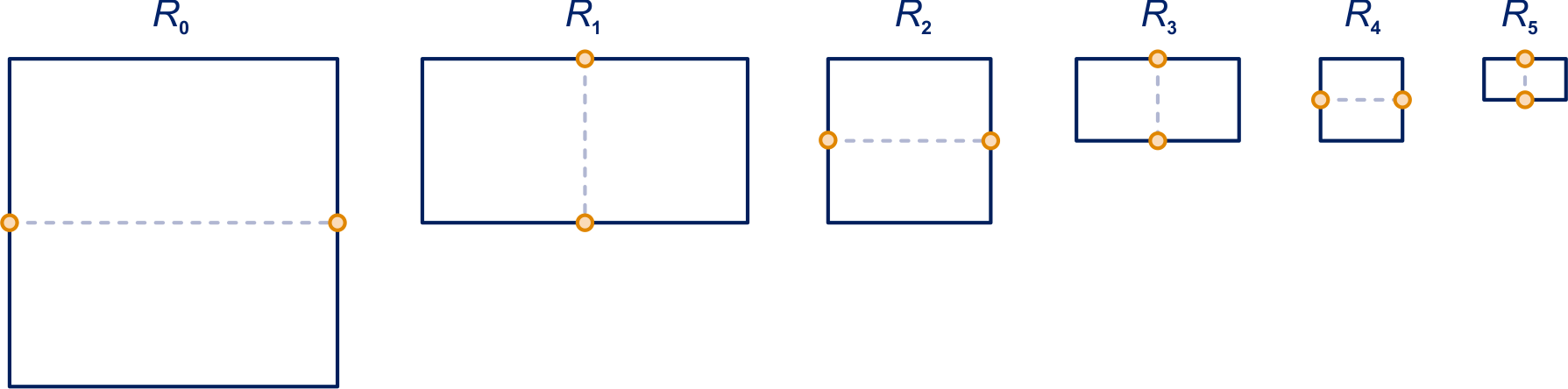
De korte zijde van $R_0$ is $x$ en de lange zijde is $2$.

$x\cdot x=2$, ofwel $x^2=2$

$x=\sqrt{2}\approx \mathrm{1,41}$

$10$ keer zo groot, dus dan $x=10\cdot \sqrt{2}$.

$a$ keer zo groot, dus dan $x=a\cdot \sqrt{2}$.

$\text{breedte}:\text{lengte}=1:\sqrt{2}$

$a\cdot a\sqrt{2}=a^2\cdot \sqrt{2}=1$
$\to$ $a^2=\frac{1}{\sqrt{2}}\approx \mathrm{0,707...}$,
dus $a=\sqrt{\mathrm{0,707...}}\approx \mathrm{0,841}$ m.
De korte zijde is $\mathrm{0,841}$ m = $841$ mm.
De lange zijde is $\sqrt{2}\cdot \mathrm{0,841}\approx \mathrm{1,189}$ m = $1189$ mm.

Oppervlakte A1-vel = $\mathrm{0,5}$ m²;
Afmetingen: $\mathrm{594,5}$ mm bij $841$ mm.

Zie tabel bij vraag c.

$2^5=32$ stuks

Gebruik verhouding = $\sqrt{2}\approx \mathrm{1,414}$
en factor = $\sqrt{\frac{1}{2}}=\frac{1}{\sqrt{2}}\approx \mathrm{0,707}$.

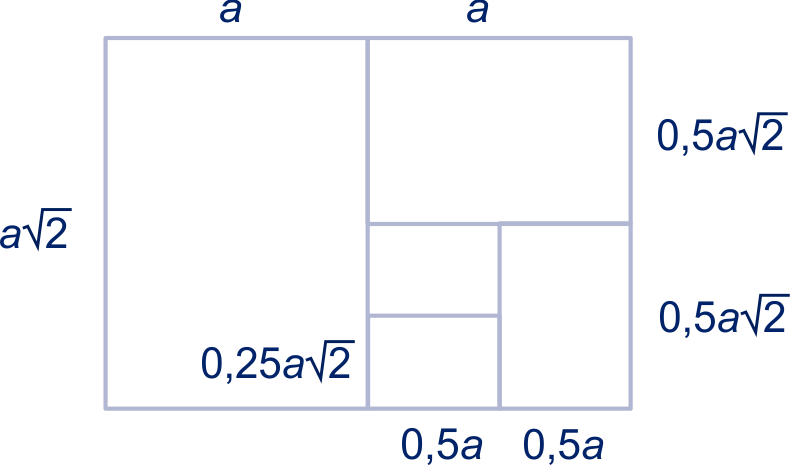
Begin met een A-formaat met afmetingen $a$ bij $a\sqrt{2}$; de langste zijde wordt gehalveerd (dus $a\sqrt{2}$ wordt $\frac{1}{2}a\sqrt{2}$) en de breedte wordt de nieuwe lengte;
De horizontale rechthoek heeft afmetingen $\frac{1}{2}a\sqrt{2}$ bij $a$;
De volgende rechthoek heeft afmetingen $\frac{1}{2}a$ bij $\frac{1}{2}a\sqrt{2}$;
Het gat heeft breedte $\frac{1}{2}a$ en dat is precies de lengte van het vierde A-formaat.

Invullen verhouding $v=\sqrt{2}$ geeft:
$f=\frac{‐1+\sqrt{1+4{(\sqrt{2})}^2}}{2\cdot \sqrt{2}}=\frac{‐1+\sqrt{9}}{2\cdot \sqrt{2}}=\frac{‐1+3}{2\cdot \sqrt{2}}=\frac{2}{2\cdot \sqrt{2}}=\frac{1}{\sqrt{2}}$, dus klopt.

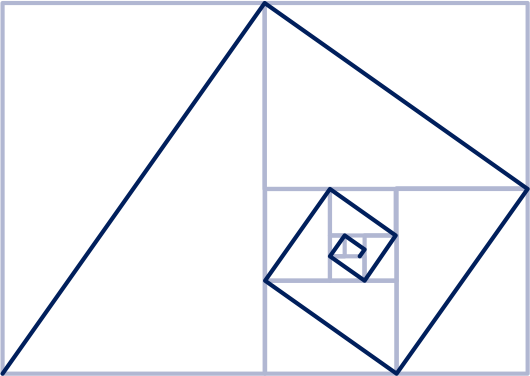
Twee opeenvolgende grijze diagonalen ontstaan door de bijbehorende A-formaten twee keer dubbel te vouwen. De diagonaal is dan gehalveerd.
Of: de lengtevergrotingsfactor van twee opeenvolgende A-formaten is $\frac{1}{\sqrt{2}}$; dus twee stappen verder is de lengtevergrotingsfactor ${\left(\frac{1}{\sqrt{2}}\right)}^2=\frac{1}{2}$, dus de diagonaal is dan gehalveerd.
Of: Van A0 naar A1, van A1 naar A2, etc. wordt de oppervlakte gehalveerd. Na twee stappen is de oppervlaktevergrotingsfactor $\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$. De lengtevergrotingsfactor is dan $\sqrt{\frac{1}{4}}=\frac{1}{2}$, dus de diagonaal is dan gehalveerd.

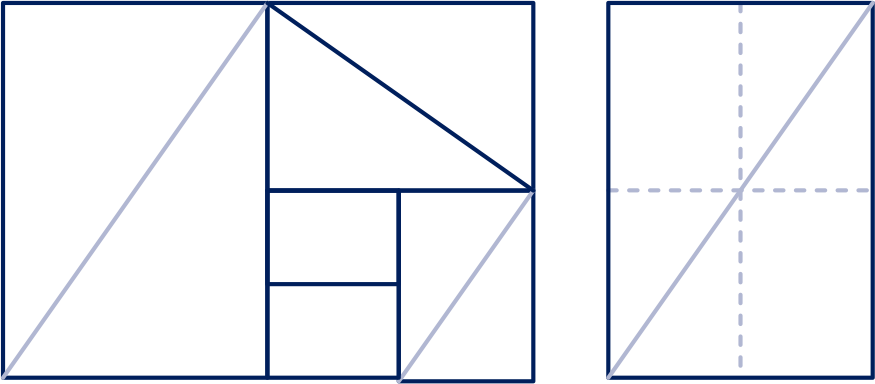
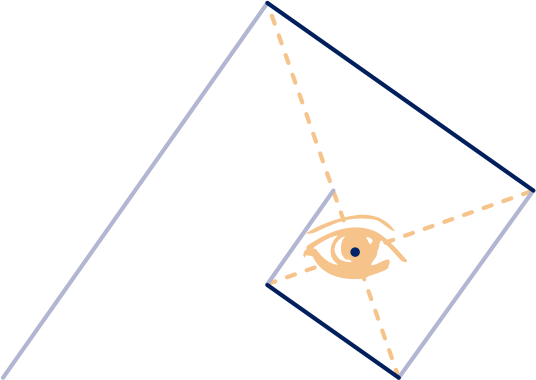
Verbind de knikken door één knik over te slaan met een rechte lijn. Het snijpunt is het oog van de spiraal.