De rechthoeken zijn niet gelijkvormig, maar dat is m.b.v. de diagonalen (evenwijdig of loodrecht) lastig te zien. Berekeningen moeten uitkomst bieden.

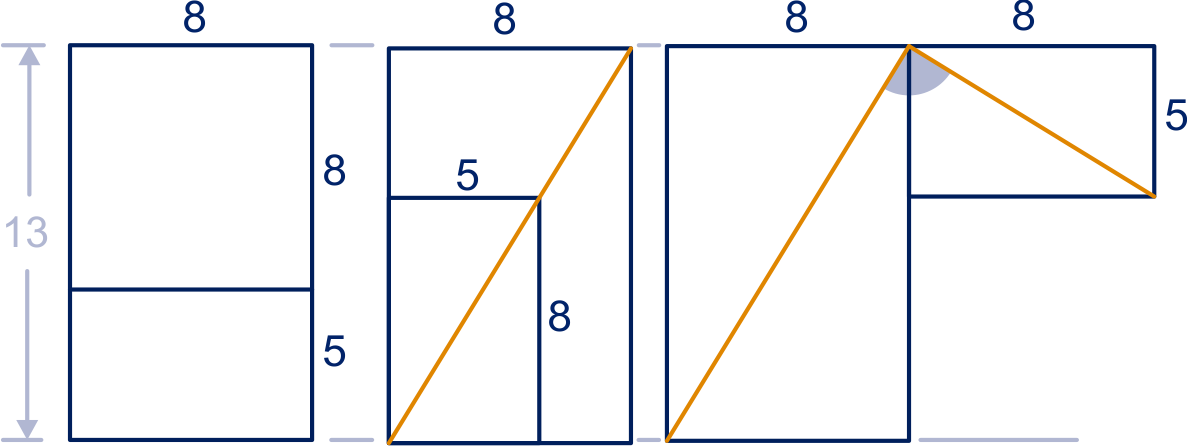
Grote rechthoek: $\frac{\text{lengte}}{\text{breedte}}=\frac{13}{8}=1\frac{5}{8}=\mathrm{1,625}$;
Kleinere rechthoek: $\frac{\text{lengte}}{\text{breedte}}=\frac{8}{5}=1\frac{3}{5}=\mathrm{1,6}$

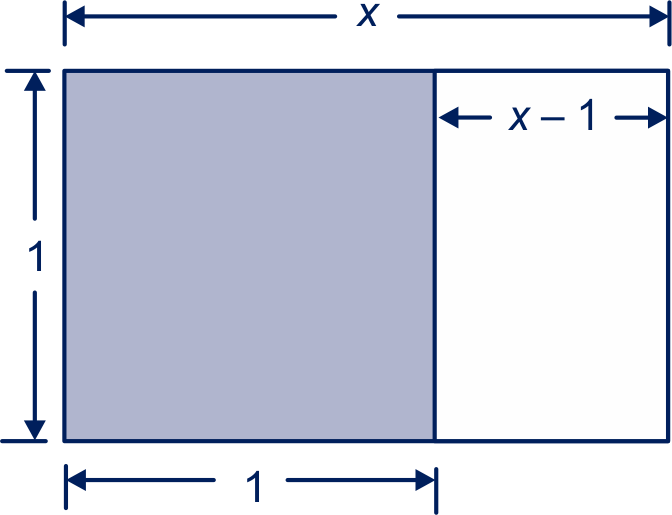
De zijden van de overgebleven rechthoek zijn $x-1$ en $1$.

De korte zijde van de grote rechthoek is vermenigvuldigd met $(x-1)$, dus de lange zijde van de grote rechthoek moet ook hiermee vermenigvuldigd worden.
De lengte van de lange zijde van de kleine rechthoek wordt dan $x\cdot (x-1)$.
Maar de lengte van de lange zijde van de kleine rechthoek is gelijk aan $1$. Dus geldt: $x\cdot (x-1)=1$.

$x\cdot (x-1)=1$ $\to$ $x^2-x=1$ $\to$ $x^2-x-1=0$

De abc-formule geeft dat de positieve waarde voor $x$ is: $x=\frac{1+\sqrt{5}}{2}=\frac{1}{2}+\frac{1}{2}\sqrt{5}\approx \mathrm{1,618}$

Opmeten en de verhouding van de twee stukken uitrekenen; $\frac{\text{lang}}{\text{kort}}\approx \mathrm{1,62}$

Opmeten en de verhouding van de twee stukken uitrekenen; $\frac{\text{lang}}{\text{kort}}\approx \mathrm{1,62}$

Als je een lengte verdeelt die zich verhouden als $2:3$, dan wordt het ene stuk het $\frac{2}{5}$ deel en het andere stuk het $\frac{3}{5}$ deel.
Dus als je een lengte verdeelt die zich verhouden als $1:\text{φ}$, dan wordt het ene stuk $\frac{1}{1+\text{φ}}$ deel van het lijnstuk en het andere deel het $\frac{\text{φ}}{1+\text{φ}}$ deel.
Dus voor het verdelen van een vierkant met zijde $6$ wordt de zijde verdeeld in stukken met lengtes $\frac{1}{1+\text{φ}}\cdot 6\approx \mathrm{2,29}$ cm en $\frac{\text{φ}}{1+\text{φ}}\cdot 6\approx \mathrm{3,71}$ cm.

De stukken zijn $\frac{1}{1+\text{φ}}\cdot 8\approx \mathrm{3,06}$ cm en $\frac{\text{φ}}{1+\text{φ}}\cdot 8\approx \mathrm{4,94}$ cm.

De quotiënten geven nagenoeg de gulden verhouding weer.

De sommen van opeenvolgende getallen geven de daaropvolgende waarde.

Boven $a$ staat $a\cdot \text{φ}$; daarboven staat $a\cdot \text{φ}\cdot \text{φ}=a\cdot {\text{φ}}^2$

$\text{φ}\cdot a$ ligt boven $a$. Daar weer boven ligt ${\text{φ}}^2\cdot a$. Twee opeenvolgende waarden levert de nieuwe waarde op, dus $a+\text{φ}\cdot a={\text{φ}}^2\cdot a$.