Er zijn twee getallen tussen en
zo dat .
Welke waarden zijn dat?
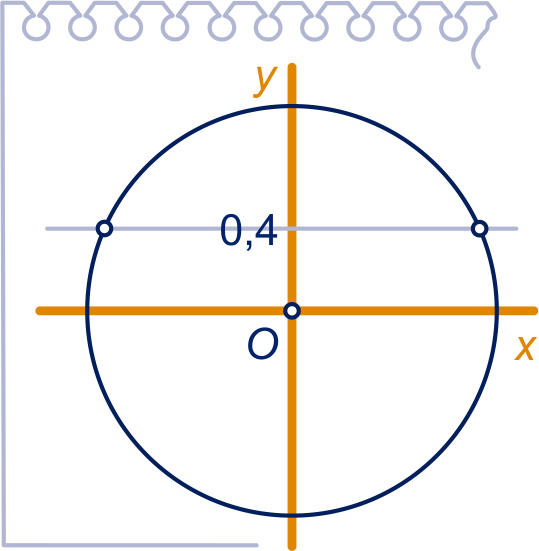
In het plaatje hiernaast zijn de bijbehorende punten op de eenheidscirkel aangegeven.
Je rekenmachine levert je één van deze twee waarden via de inverse van de sinus:
.
De andere waarde vind je door het bijbehorende punt te spiegelen in de -as: .
Bereken (in drie decimalen nauwkeurig) de getallen
tussen en waarvoor de volgende waarden heeft.
Teken eventueel een plaatje in de eenheidscirkel.
In het voorbeeld hierboven heb je de getallen gevonden tussen en waarvoor geldt: .
Geef ook de getallen tussen en met
.
En de getallen tussen
en
met .
Alle oplossingen van de vergelijking zijn:
en
met
geheel. Zie opgave 40.
Er zijn twee getallen tussen
en zo dat .
Welke waarden zijn dat?
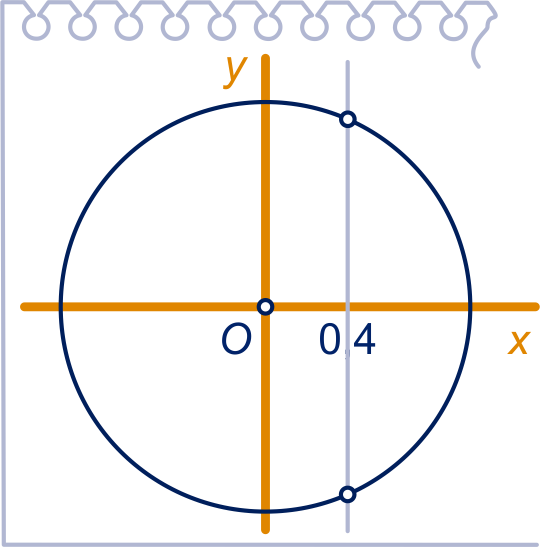
In het plaatje hiernaast zijn de bijbehorende punten op de eenheidscirkel aangegeven. Je rekenmachine levert je één van deze twee waarden:
.
Door het bijbehorende punt te spiegelen in de -as, vind je nog een oplossing: .
De andere oplossing tussen en is:
.
Bereken de getallen tussen en waarvoor de de volgende waarden heeft. Teken eventueel een plaatje in de eenheidscirkel.
Twee kogeltjes bewegen, het eerste volgens:
het tweede volgens: .
Geef op de eenheidscirkel zo nauwkeurig mogelijk de punten aan waar het eerste kogeltje is als beide kogeltjes op gelijke hoogte zijn. (Dat zijn vier plaatsen.)
Bepaal exact de tijdstippen tussen en waarbij de kogeltjes gelijke hoogte hebben.
Gegeven twee functies: en .
Teken de grafieken van beide functies op de GR.
Geef van beide de periode.
De vergelijking heeft als exacte oplossing.
Controleer dat zonder je rekenmachine te gebruiken.
De tekening van de grafieken op de GR doet vermoeden dat de oplossingen van de vergelijking ook periodiek zijn.
Heb je een vermoeden over de periode?
Bepaal de exacte oplossingen van de vergelijking:
voor
(bijvoorbeeld met behulp van je vermoeden).
Als je dit moeilijk vindt, kun je deze vraag meer rekentechnisch oplossen: zie voorbeeld 1 van paragraaf 6.
Gegeven zijn twee functies: en .
Teken de grafieken van beide functies op de GR. Geef van beide de periode.
Los op zonder GR: , voor .
Gegeven zijn twee functies: en .
Teken de grafieken van beide functies op de GR. Geef van beide de periode.
Los op zonder GR: , voor .
Gegeven zijn twee functies: en .
Teken de grafieken van beide functies op de GR. Geef van beide de periode.
Los op zonder GR: , voor .
