1

Gegeven is de functie $f : x \to 5 + 2 \sin (3 (x - \frac{1}{4} π))$ .

a

Bepaal zonder GR welke waarden $y$ aan kan nemen. Licht je antwoord toe.

b

Bepaal zonder GR de oplossingen $x$ van de vergelijking $y = 4$ .
Hoeveel oplossingen zijn er als $‐ π \leq x \leq 2 π$ ?

De hoek waaronder de lijn $y = 4$ de grafiek van $f$ snijdt is in elk snijpunt hetzelfde.

c

Leg dat uit en bereken de hoek in graden nauwkeurig.

2

Een kogeltje beweegt volgens ${\begin{cases} x = 1 + 2 \cos (3 t - \frac{1}{2} π) \\ y = 5 + 2 \sin (3 t - \frac{1}{2} π) \end{cases}$ .

a

Welke beweging wordt door deze parametervoorstelling beschreven? (Baan, hoeksnelheid, startpunt, snelheid?)

b

Bereken exact de momenten $t$ tussen $0$ en $6$ waarop het kogeltje op hoogte $6$ is.

3

Gegeven is de cirkelbeweging: ${\begin{matrix} x = 3 + 2 \cos (π (1 - t)) \\ y = 4 + 2 \sin (π (1 - t)) \end{matrix}$ .

a

Geef middelpunt, straal, periode en fasehoek van de beweging.

b

Wat is de grootte van de snelheid van het kogeltje als de afstanden in meters en de tijd in seconden gemeten wordt?

4

Geef een parametervoorstelling van het kogeltje dat met een hoeksnelheid van $π$ rad/s beweegt over de cirkel met straal $2$ en middelpunt $(1, ‐ \sqrt{3})$ , tegen de wijzers van de klok in en dat op $t = 0$ in $O (0,0)$ is ( $t$ in seconden).

5

Een kogeltje gaat in $4 π$ seconden een cirkel met straal $3$ rond.

a

Wat is de hoeksnelheid (in rad/s) en de snelheid van dat kogeltje?

Op zeker moment is het kogeltje op een hoogte die het $π$ seconden later weer heeft.

b

Bereken exact hoe ver die punten van elkaar liggen.

6

a

Bereken zonder rekenmachine $\cos (t)$ als $\sin (t) = 0,96$ en $t$ tussen $\frac{1}{2} π$ en $π$ ligt.

b

Bereken in drie decimalen nauwkeurig alle waarden van $t$ tussen $‐ π$ en $π$ als $\sin^{2} (t) = 0,36$ .

c

Leg uit dat $\cos (\frac{3}{8} π) = \sin (\frac{1}{8} π) = \sin (\frac{7}{8} π)$ .

7

Gegeven zijn: α en β tussen $\frac{1}{2} π$ en $π$ met: $\sin (α) = \frac{1}{5} \sqrt{5}$ en $\sin (β) = \frac{1}{2}$ .

Bereken zonder rekenmachine $\sin (α + β)$ , $\cos (α - β)$ , $\sin (2 α)$ en $\cos (2 α)$ .

8

Een kogeltje beweegt volgens ${\begin{matrix} x = t \cos (t) \\ y = t \sin (t) \end{matrix}$ , met $t > 0$ .

a

Bepaal de snelheidsvector bij de beweging.

b

Bereken het moment waarop de snelheid van het kogeltje $3$ is exact.

9

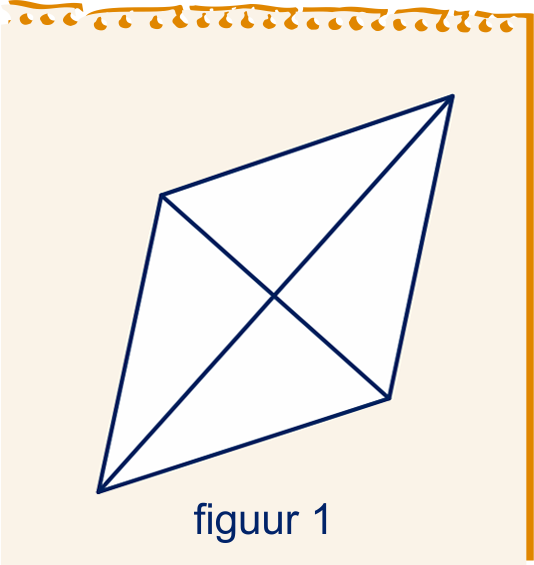
De ruit in figuur 1 heeft zijden van lengte $1$ . De scherpe hoeken zijn $2 α$ .

a

Druk de lengte van de diagonalen uit in α.

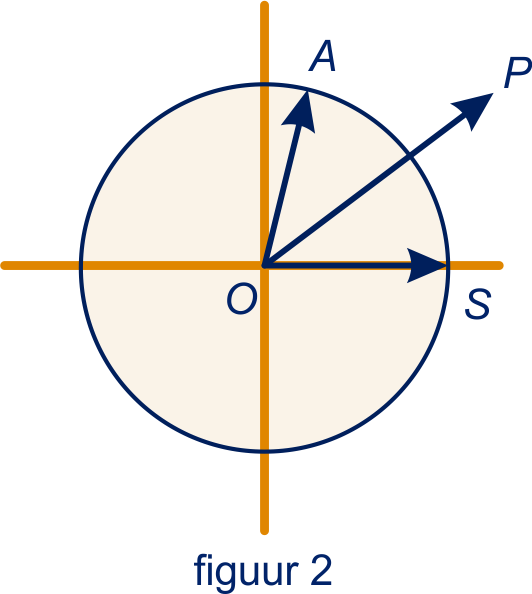
In figuur 2 staat de eenheidscirkel met $S (1,0)$ , $A (\cos (2 α), \sin (2 α))$ en $\vec{O P} = \vec{O S} + \vec{O A}$ .
Er is een getal $k$ met $\vec{O P} = k \cdot (\begin{matrix} \cos (α) \\ \sin (α) \end{matrix})$ .

b

Waarom?

c

Bepaal het getal $k$ exact.

d

Laat zien dat hieruit de verdubbelingsformules volgen.

10

We gaan verder met de vorige opgave.
De helling van lijn $O P$ noemen we $m$ .
Er geldt: $m = \frac{\sin (α)}{\cos (α)}$ .

a

Ga dat na.

b

Laat zien: de helling van lijn $O A$ is: $\frac{2 \sin (α) \cdot \cos (α)}{\cos^{2} (α) - \sin^{2} (α)}$ .

In hoofdstuk 9 (verdubbeling van de hellingshoek) zul je zien: de helling van lijn $O A$ is: $\frac{2 m}{1 - m^{2}}$ .

c

Leid dit af uit b.

11

Bewijs de volgende goniometrische identiteiten.

$\frac{\cos (2 x) + \cos (x)}{\cos (x) + 1} = 2 \cos (x) - 1$ en
$\cos (x - y) \cos (x + y) = \cos^{2} (y) - \sin^{2} (x)$ .

12

Twee kogeltjes bewegen, het een volgens: ${\begin{cases} x = \cos (t) + 1 \\ y = \sin (t) \end{cases}$ en het ander volgens ${\begin{cases} x = 2 \cos (2 t) + 4 \\ y = 2 \sin (2 t) \end{cases}$ .

a

Bereken in twee decimalen nauwkeurig de tijdstippen $t$ met $0 \leq t \leq 2 π$ dat de kogeltjes op dezelfde hoogte zijn.

b

Bereken de tijdstippen tussen $0$ en $2 π$ dat je de kogeltjes vanuit de oorsprong $(0,0)$ in dezelfde richting ziet.

13

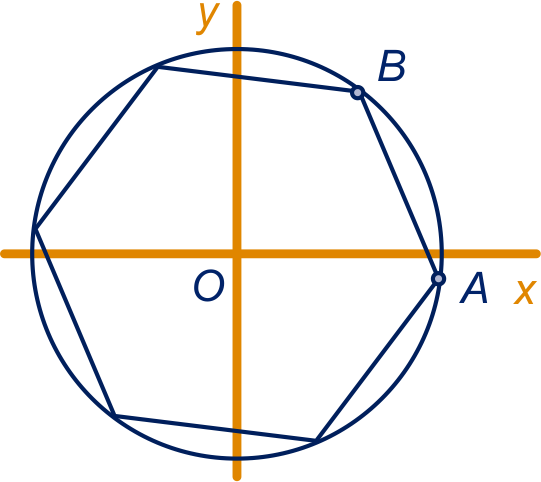
Op de eenheidscirkel liggen de hoekpunten van een regelmatige zeshoek. Eén van de hoekpunten is $B (\frac{3}{5}, \frac{4}{5})$ .

Bereken exact de coördinaten van hoekpunt $A$ , zie figuur.
Gebruik de somformules.

14

Gegeven is de functie $f$ met $f (x) = \cos^{2} (x) + \cos (x)$ op $[‐ π, π]$ .

a

Bereken exact de nulpunten van $f (x)$ .

b

Bereken de extreme waarden van $f (x)$ exact.