4.11 Opdrachten

Hoofdstukken > Hoeken en bogen

In deze paragraaf stellen we vier "klassiekers" uit de meetkunde aan de orde. Zij lenen zich uitstekend om leerlingen een presentatie in de klas te laten geven.
Er zijn geen antwoorden bij de opdrachten opgenomen.

Gegeven is driehoek $A B C$ . $H$ is zijn hoogtepunt.
De voetpunten van de hoogtelijnen zijn: $D$ , $E$ en $F$ .
De middens van de zijden zijn: $P$ , $Q$ en $R$ .
De middens van $A H$ , $B H$ en $C H$ zijn: $U$ , $V$ en $W$ .

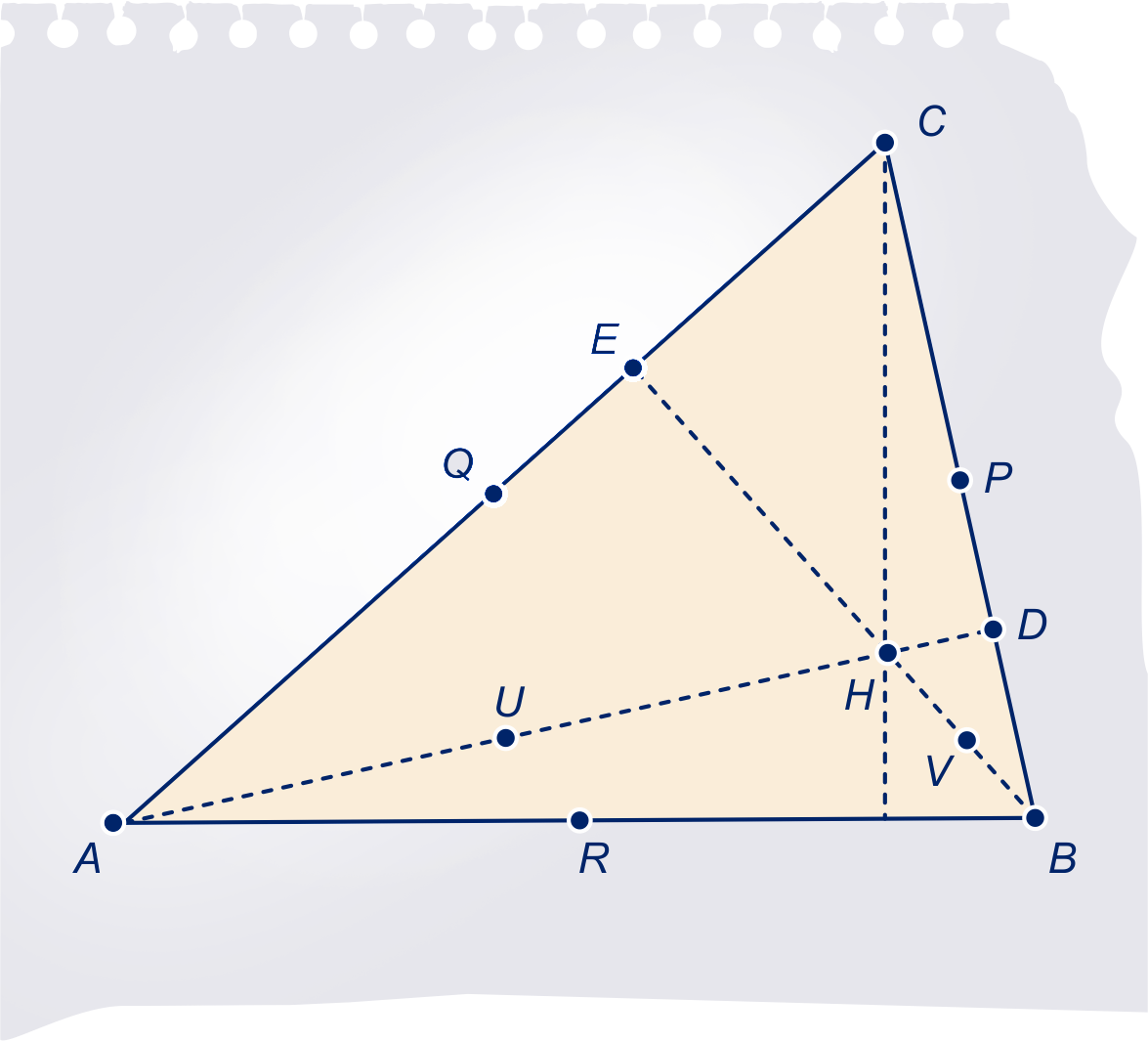
Bewijs dat de negen punten $D$ , $E$ , $F$ , $P$ , $Q$ , $R$ , $U$ , $V$ en $W$ op één cirkel liggen.

(hint)

Het middelpunt van de omgeschreven cirkel van driehoek $P Q R$ noemen we $N$ .
Bewijs dat $| N R | = | N F |$ .
Bewijs dat $N$ op de middelloodlijn van lijnstuk $U V$ ligt en dat driehoek $U W V$ congruent is met driehoek $P Q R$ .

Karl Wilhelm Feuerbach (1800 - 1834) was professor in Erlangen (Duitsland). Hij is vooral bekend geworden door de negenpuntscirkel. Hij bewees ook dat deze raakt aan zowel de ingescheven als de drie aangescheven cirkels van de driehoek.
Feuerbach had een slechte gezondheid en stierf jong.

De rechte van Wallace
Gegeven is driehoek $A B C$ met zijn omgeschreven cirkel.
$P$ is een punt van die omgeschreven cirkel. De voetpunten van de loodlijnen uit $P$ op $A B$ , $B C$ en $C A$ noemen we achtereenvolgens $C^{'}$ , $A^{'}$ en $B^{'}$ .

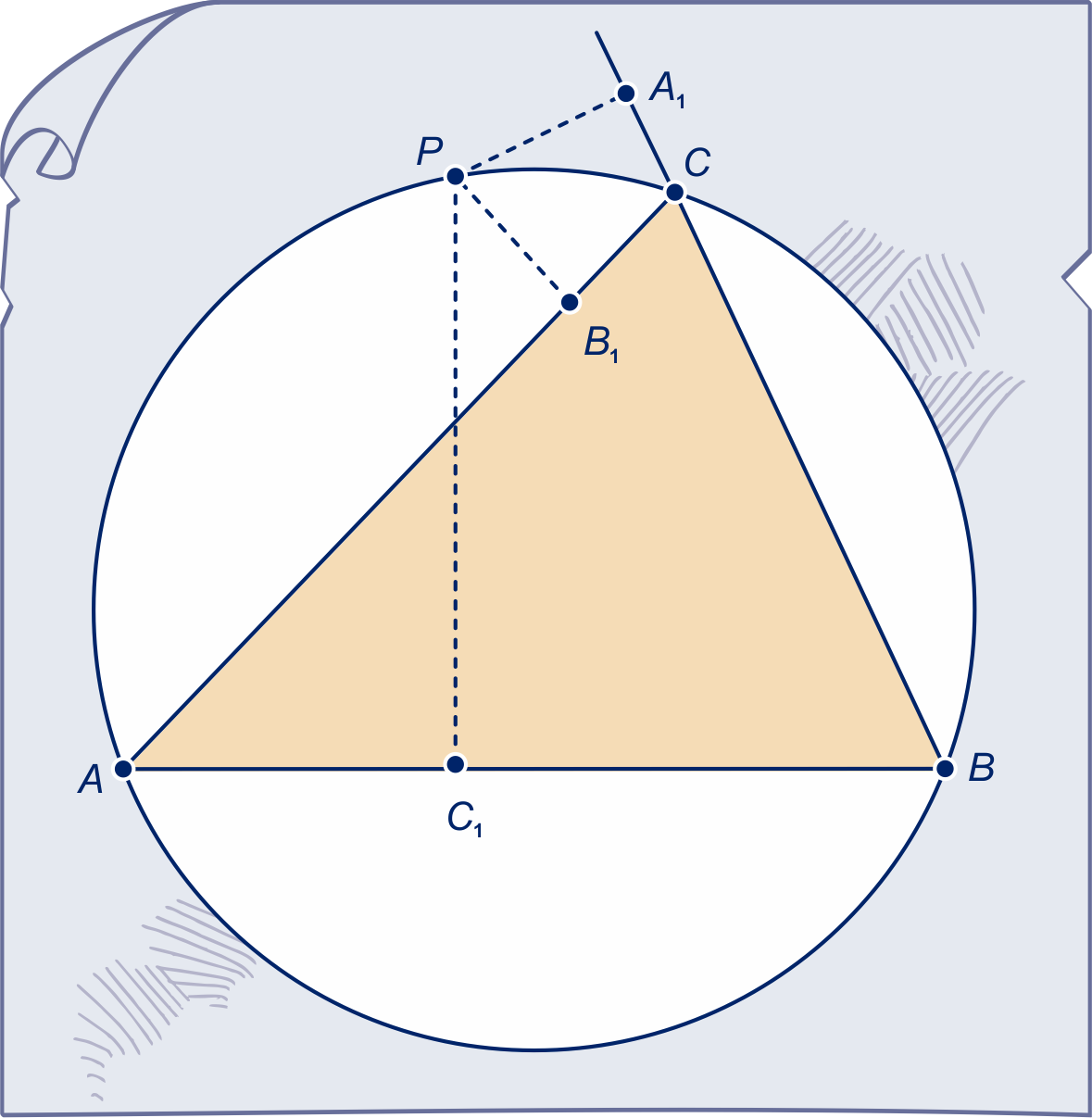
Bewijs dat $A^{'}$ , $B^{'}$ en $C^{'}$ op één lijn liggen.

(hint)

Bewijs dat

∠ A^{'} P C = ∠ C^{'} P A

.
Bewijs dat de cirkel door

P

C

A^{'}

en de cirkel door

P

A

C^{'}

elkaar snijden in

B^{'}

.
Bewijs dat

∠ A^{'} B^{'} C = ∠ A^{'} P C

∠ C^{'} B^{'} A = ∠ C^{'} P A

William Wallace (1768 - 1843) was een Schots autodidact. Hij was professor in Great Marlow en Edinburgh. Van hem is ook de volgende stelling afkomstig.
Gegeven zijn vier lijnen waarvan elk drietal een driehoek insluit. Dan hebben de omgeschreven cirkels van deze vier driehoeken een gemeenschappelijk punt.
Wallace heeft ook de Pantograaf uitgevonden, zie het hoofdstuk Gelijkvormigheid in de tweede klas.

De punten van Brocard
Gegeven is driehoek $A B C$ .
$c_{1}$ is de cirkel die in $C$ aan $C A$ raakt en door $B$ gaat,
$c_{2}$ is de cirkel die in $A$ aan $A B$ raakt en door $C$ gaat,
$c_{3}$ is de cirkel die in $B$ aan $B C$ raakt en door $A$ gaat.

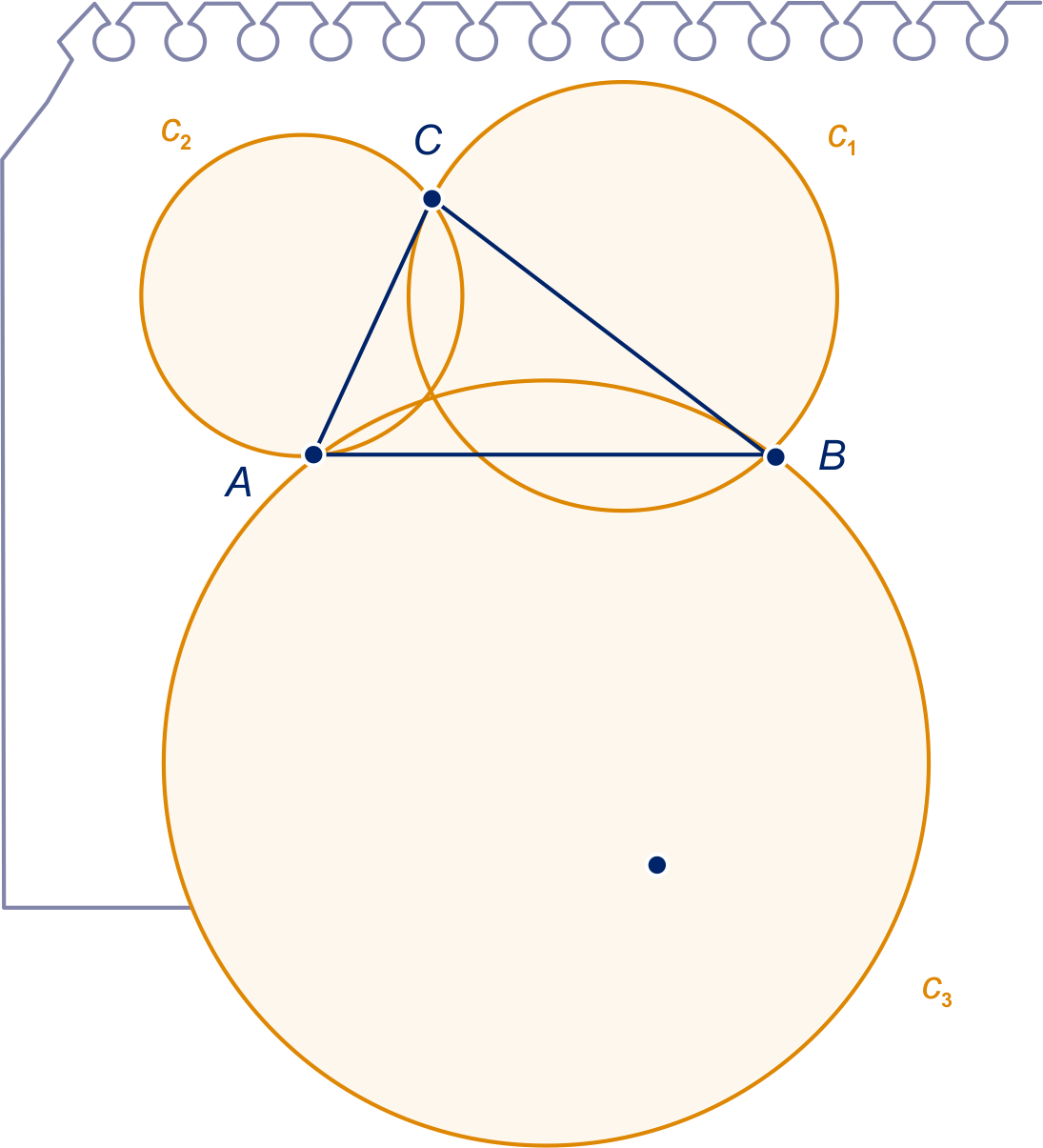
Bewijs dat $c_{1}$ , $c_{2}$ en $c_{3}$ door één punt gaan: een punt van Brocard.

Er is nòg een punt van Brocard, namelijk het snijpunt van:
de cirkel $d_{1}$ die in $C$ aan $C B$ raakt en door $A$ gaat,
de cirkel $d_{2}$ die in $A$ aan $A C$ raakt en door $B$ gaat,
de cirkel $d_{3}$ die in $B$ aan $B A$ raakt en door $C$ gaat.

Henri Brocard (1845 - 1922) was een Frans legerofficier. Hij was een amateur wiskundige. Over de naar hem genoemde punten is nog veel meer te zeggen.
Wel heel fraai is het volgende. Drie hondjes A, B en C zitten in de hoekpunten van een driehoek. Op hetzelfde moment beginnen ze met dezelfde snelheid te rennen: A naar B, B naar C en C naar A. Op elk moment is hun looprichting naar de staart van hun voorganger. De hondjes zullen elkaar dan ontmoeten in een van de Brocard-punten van de driehoek. Als de looprichting wordt omgekeerd, eindigen ze in het andere Brocard-punt.

De stelling van Napoleon
Gegeven is driehoek $A B C$ . Plaats op de zijden drie driehoeken die gelijkvormig zijn, zo dat ze bij $A$ met even grote hoeken liggen, ook bij $B$ en ook bij $C$ . De tophoeken, tegenover $A$ , $B$ en $C$ noemen we achtereenvolgens $A^{'}$ , $B^{'}$ en $C^{'}$ .

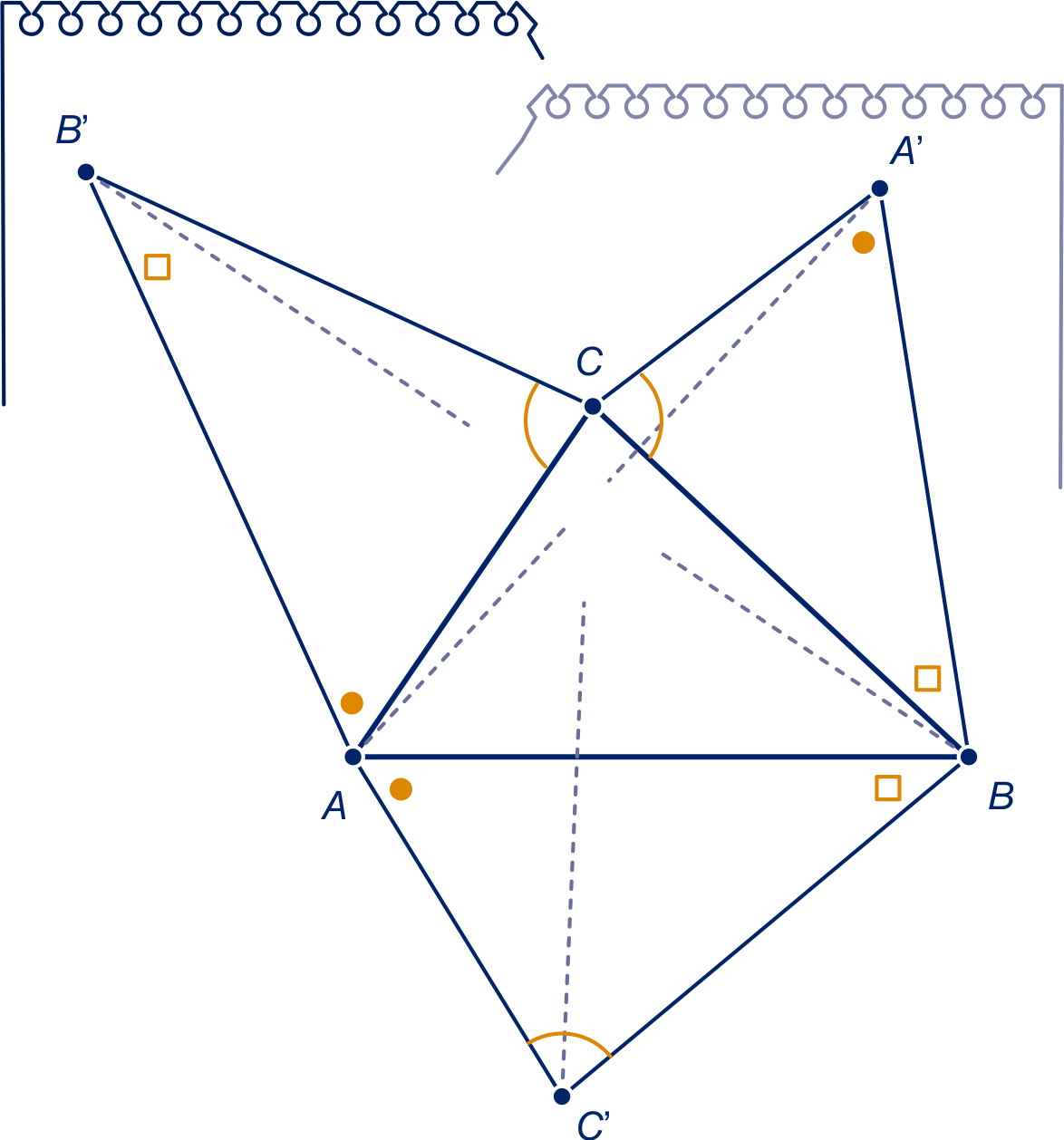
Ga nog eens na dat de omgeschreven cirkels van deze gelijkvormige driehoeken door één punt gaan.

Bewijs dat de lijnen $A A^{'}$ , $B B^{'}$ en $C C^{'}$ door datzelfde punt gaan.

Of bovenstaande stelling inderdaad van Napoleon Bonaparte (1769 - 1821) afkomstig is, is onzeker. Het is niet onmogelijk, want Napoleon heeft een degelijke wiskunde opleiding genoten. Sommigen schrijven niet bovenstaande stelling aan Napoleon toe, maar de volgende.
Gegeven is een driehoek. Plaats op de zijden gelijkzijdige driehoeken, naar buiten of naar binnen. De middelpunten daarvan zijn dan de hoekpunten van een gelijkzijdige driehoek.

Meer soortgelijke opgaven vind je in Denken in cirkels en lijnen van het Freudenthal Instituut te Utrecht.