Los de volgende vergelijkingen in exact op.
|
|
|
|
|
|
Gegeven een complex getal .
Wat is het verband tussen en ?
We bekijken de vergelijking . De oplossing van deze vergelijking met het kleinste positieve argument noemen we .
Druk en uit in machten van .
We schrijven
Toon 'meetkundig' en 'algebraïsch' aan dat oplossing is van de vergelijking .
Druk de oplossingen van in machten van uit.
Gegeven zijn de getallen en
met:
,
,
en
.
Schrijf in de vorm met en exact.
Bereken exact: .
Schrijf in de vorm met en exact.
Er geldt: .
Reken dat na.
Geef alle oplossingen van de vergelijking exact in de vorm.
Bereken exact .
Gegeven is de vergelijking .
Laat zien: als het complexe getal aan de vergelijking voldoet dus , dan voldoet ook , dus dan ook .
Je kunt narekenen dat
oplossing van de vergelijking is, dus ook
.
Volgens de hoofdstelling van de algebra geldt dan:
.
Bereken exact.
Wat zijn de oplossingen van de vergelijking ?
De volgende opgave komt ook voor in 4vb hoofdstuk 5.
Nu moet je de oplossing zoeken met behulp van complexe getallen.
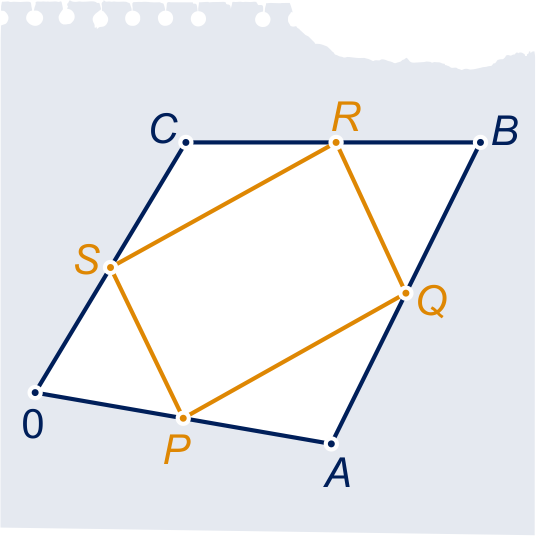
is een vierhoek, de middens van de zijden zijn , , en .
Toon met een berekening met complexe getallen aan dat vierhoek een parallellogram is.
Schatgraven op Teleurstellingseiland
Op een onooglijk stukje vergeeld papier dat Anne in een oude kist vindt, staat het volgende.

Ze trekt zich niets aan van de gruwelverhalen op Wikipedia.
Het eiland ligt op , .: Disappointment Island; een van de onbewoonde Auckland Islands ten zuiden van Nieuw Zeeland. Onbewoond? Op visverwerkende witkopalbatrossen na!
Anne heeft vast een plan gemaakt, voor als ze de stenen en de stronk eenmaal heeft gevonden.
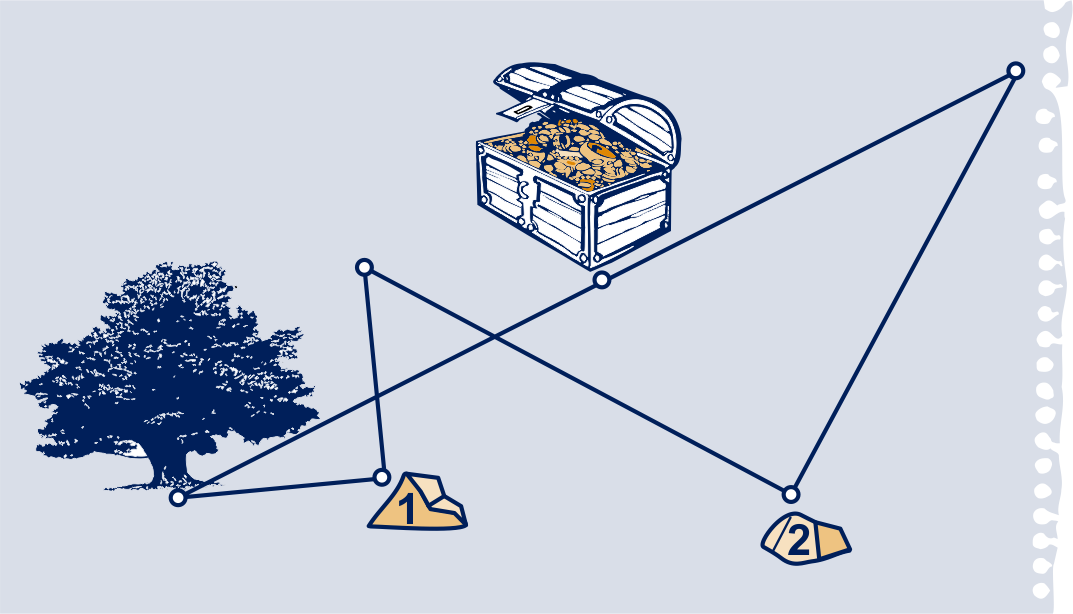
Op Teleurstellingseiland aangekomen, vindt ze wel de twee stenen, maar de stronk van de oude eik is vergaan.
Neem een stuk papier en teken daarop twee punten. Daar liggen de stenen. Kies nu een willekeurig derde punt voor de positie van de stronk en voer de zoekactie uit met je geodriehoek.
Kies nog een ander punt voor de stronk en voer de zoekactie nog eens uit.
Je kunt de zoekactie ook bekijken met de GeoGebra applet
"Schatzoeken".
Het lijkt wel of de plaats van de schat niet van de plaats van de stronk afhangt!
Dat dit inderdaad zo is, kun je als volgt inzien.
Neem een assenstelsel zo dat de stenen in de punten en
liggen.
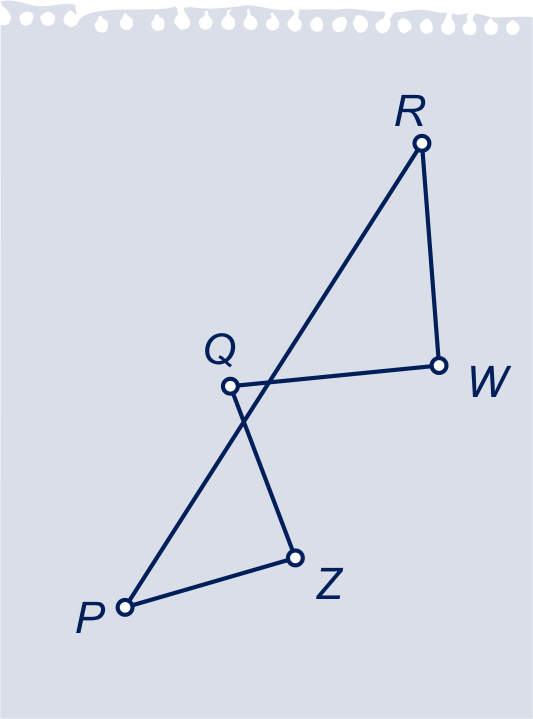
Druk de getallen en (zie plaatje) in , en uit.
Laat zien dat het midden van niet afhangt van de keuze van .
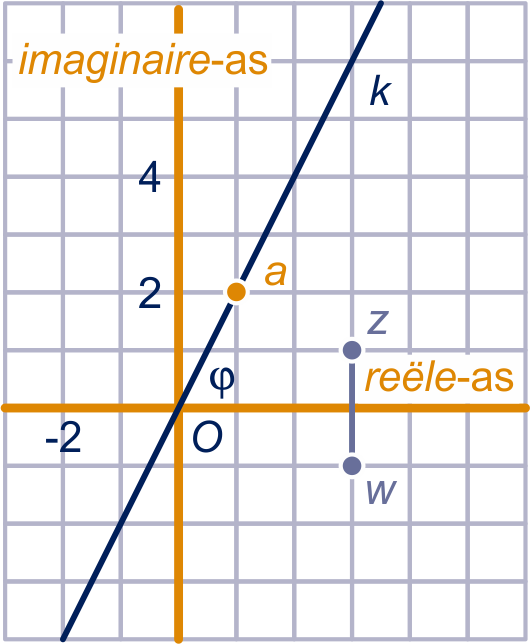
De punten ,
en
zijn roosterpunten. en het spiegelbeeld van in de reële as is
.
is de lijn door de punten
en .
Vermenigvuldigen met is linksom draaien over hoek
om gevolgd door een puntvermenigvuldiging
ten opzichte van .
Met welke factor?
Teken de beelden en van en 'meetkundig', dus met behulp van het voorgaande.
Ga na of je het beeld van goed getekend hebt door te berekenen.
en zijn elkaar spiegelbeeld in .
Bereken (schrijf in de vorm ) het spiegelbeeld van in .
Wat we in Extra opgave 8 gedaan hebben geldt ook voor andere complexe getallen .
Gegeven zijn de complexe getallen en , dan is het spiegelbeeld van in de lijn .
Neem aan dat unitair is, dan .
Het spiegelbeeld van een complex getal vind je als volgt.
Zoek het getal met , dan is het spiegelbeeld van
:
.
Gegeven de complexe getallen en
.
Dan is het spiegelbeeld van in lijn :
.
Ga na dat bovenstaande juist is voor de spiegeling in de imaginaire as.
Ga na dat bovenstaande juist is voor de spiegeling in de lijn (de lijn ).
Bij spiegelen in de lijn is het beeld van gelijk aan .
Toon dat aan.
Bij een lijnspiegeling in een lijn door is het spiegelbeeld van .
Druk het beeld van uit in en en ga na dat je formule als beeld van oplevert.
