$\overrightarrow{PF}=\left(\begin{array}{c}6\\ 4\\ 6\end{array}\right)$, $\overrightarrow{AH}=\left(\begin{array}{c}\mathrm{‐6}\\ 0\\ 6\end{array}\right)$

$\overrightarrow{PF}$ en $\overrightarrow{AH}$ zijn geen veelvoud van elkaar.

$C=\left(\mathrm{‐}\mathrm{4,4,0}\right)$ en $D=$$\left(\mathrm{‐4,‐4,0}\right)$

$\left(\mathrm{3,3,2}\right)$

$\overrightarrow{BT}=\left(\begin{array}{c}\mathrm{‐}4\\ \mathrm{‐}4\\ 8\end{array}\right)$ en $\overrightarrow{BP}=\left(\begin{array}{c}\mathrm{‐}1\\ \mathrm{‐}1\\ 2\end{array}\right)$

$\overrightarrow{BR}=\left(\begin{array}{c}\mathrm{‐}1\frac{1}{5}\\ \mathrm{‐}1\frac{1}{5}\\ 2\frac{2}{5}\end{array}\right)$, dus $R=\left(2\frac{4}{5}\mathrm{,2}\frac{4}{5}\mathrm{,2}\frac{2}{5}\right)$.

Een punt van $BT$ is: $\left(4-4t\mathrm{,4}-4t\mathrm{,8}t\right)$. Dit heeft gelijke $y$- en $z$-coördinaat als $4-4t=8t$, dus als $t=\frac{1}{3}$. Je krijgt het punt $\left(2\frac{2}{3}\mathrm{,2}\frac{2}{3}\mathrm{,2}\frac{2}{3}\right)$

‘Startpunt’ is $T$ en je ‘loopt’ in de richting $\frac{1}{4}\cdot \overrightarrow{BT}$.

$\left(x,y,z\right)=\left(\mathrm{‐}t,t\mathrm{,8}+2t\right)$ of $\left(x,y,z\right)=\left(2t,\mathrm{‐}2t\mathrm{,8}-4t\right)$ of ... .

Zie figuur, dat is het snijpunt van lijn $AE$ met lijn $BP$ (punt $Q$).

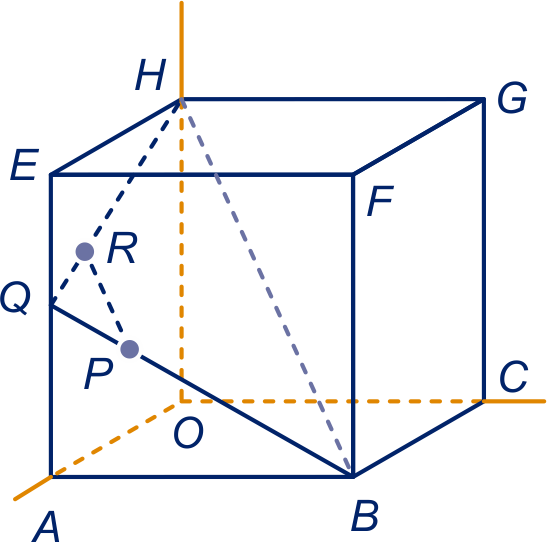
Het is punt $R$, het snijpunt van de lijn door $P$ evenwijdig met lijn $BH$ met lijn $HQ$.

Een pv van $k$ is: $\left(x,y,z\right)=\left(4+t\mathrm{,1}+t\mathrm{,2}-t\right)$.
Voor het punt $R$ geldt: $y=0\iff t=\mathrm{‐}1$, je krijgt: $\left(\mathrm{3,0,3}\right)$.

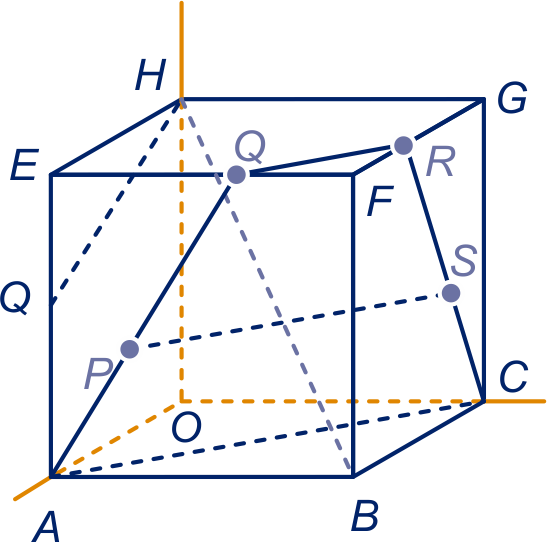
Het snijpunt is $S$. Vlak $ACP$ snijdt de bovenkant van de kubus volgens een lijn evenwijdig aan $AC$.
$S$ is zó getekend dat $SP$ evenwijdig aan $AC$ is.

Een pv van $m$ is $\left(x,y,z\right)=\left(4-t\mathrm{,1}+t\mathrm{,2}\right)$. Het punt $S$ krijg je voor $t=3$, dit geeft het punt $\left(\mathrm{1,4,2}\right)$.

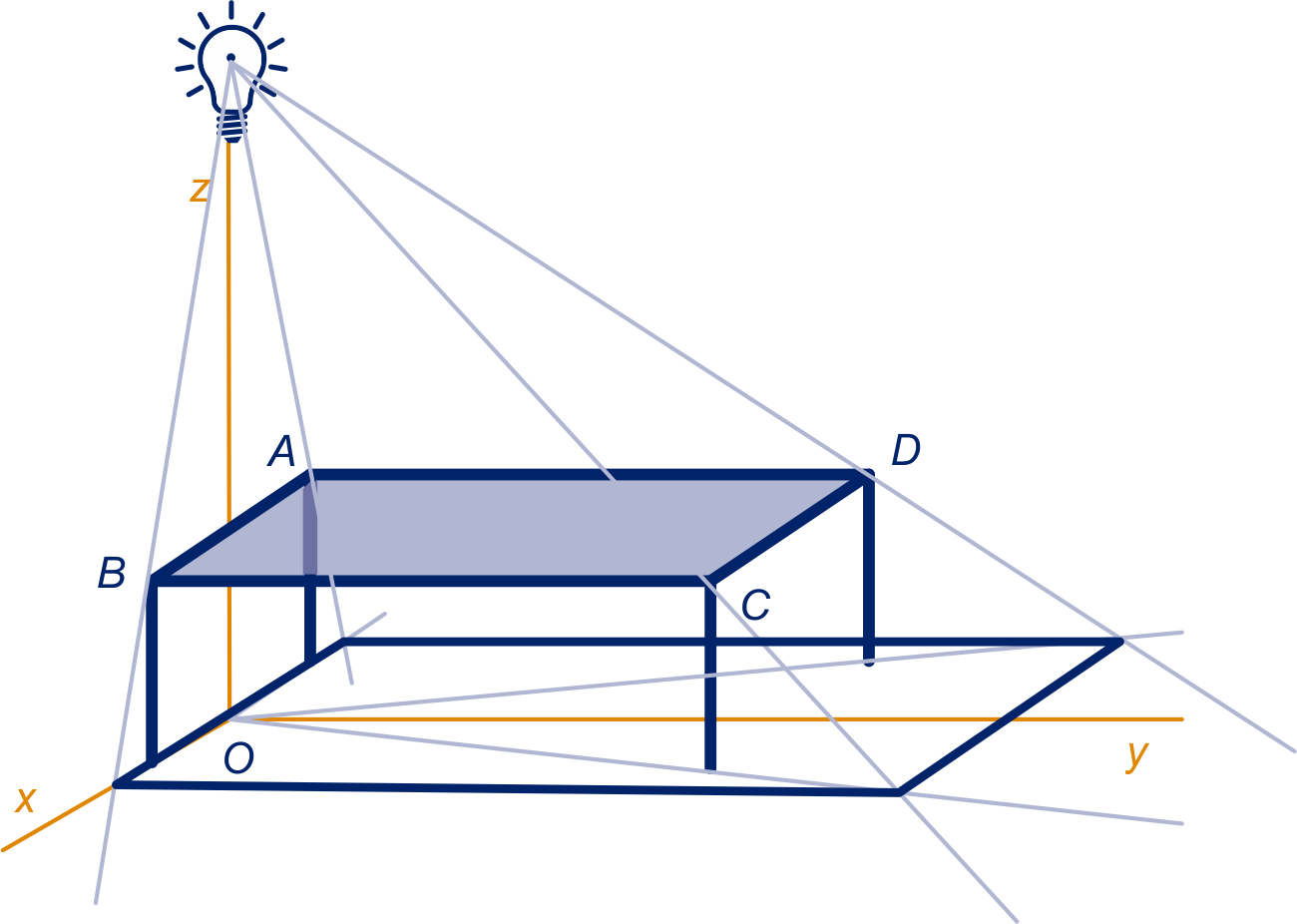
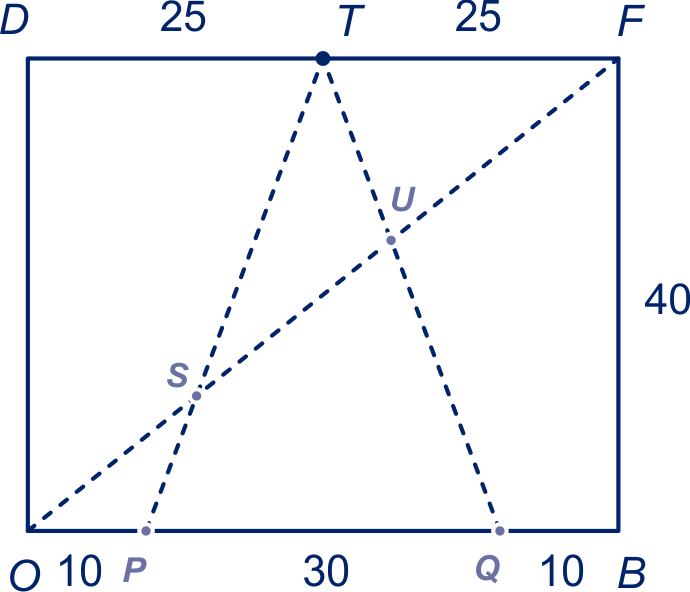
De schaduwen van $A$, $B$, $C$ en $D$ zijn $A^{\prime }$, $B^{\prime }$, $C^{\prime }$ en $D^{\prime }$. Toelichting. De schaduw $C^{\prime }$ van $C$ bijvoorbeeld vind je als volgt. Teken de lijn door $O$ en de voet van de tafelpoot bij $C$. Teken de lijn door het lichtpunt en $C$. Het snijpunt van deze twee lijnen is $C^{\prime }$.

De vergrotingsfactor van tafelblad naar schaduw is $\frac{12}{8}=1\frac{1}{2}$, de schaduw is dus $120$ bij $180$ (cm).

$\left(x,y,z\right)=\left(t\mathrm{,3}t\mathrm{,12}-2t\right)$ is een pv van lijn $LC$. De schaduw van $C$ vind je voor $t=6$, dus de schaduw is het punt $\left(\mathrm{6,18,0}\right)$.

Vanwege het feit dat het tafelblad en vloer evenwijdig zijn, krijg je een cirkel met straal $1\frac{1}{2}$ en als middelpunt $\left(\mathrm{3,4}\frac{1}{2}\mathrm{,0}\right)$ de schaduw van $\left(\mathrm{2,3,4}\right)$.

Zie de figuur hieronder.

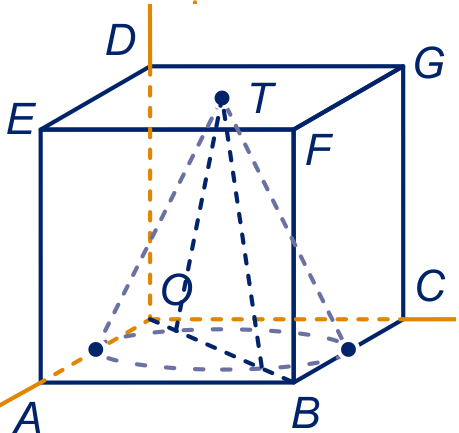
figuur bij onderdeel a

figuur bij onderdeel b

Toelichting. Lijn $OB$ snijdt de grondcirkel van de kegel in $P$ en $Q$. Vlak $OBFD$ snijdt de kegel volgens driehoek $PQT$. $S$ is het snijpunt van $PT$ en $OF$; $U$ is het snijpunt van $TQ$ en $OF$.

Zie figuur hierboven rechts.

Driehoek $TSF$ is een uitvergroting van driehoek $SOP$, de vergrotingsfactor is $\frac{TF}{OP}=2\frac{1}{2}$, dus $S$ ligt op hoogte $\frac{2}{7}\cdot 40=11\frac{3}{7}$. De hoogte van $U$ is: $\frac{8}{13}\cdot 40=24\frac{8}{13}$.

$\overrightarrow{OP}=\frac{1}{5}\overrightarrow{OB}$, dus $P=\left(\mathrm{8,6,0}\right)$.

Lijn $TP$ heeft pv $\left(x,y,z\right)=\left(8+12t\mathrm{,6}+9t\mathrm{,40}t\right)$.

$x$-coördinaat $=z$-coördinaat, want in de $x$-richting heeft het blok dezelfde afmeting als in de $z$-richting. Je krijgt $P$ dus als $8+12t=40t$, dus als $t=\frac{2}{7}$ , dus $P=\left(11\frac{3}{7}\mathrm{,8}\frac{4}{7}\mathrm{,11}\frac{3}{7}\right)$.

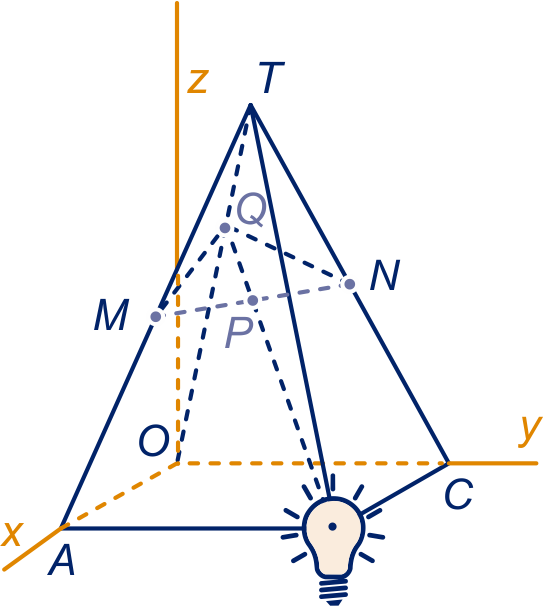
Toelichting. $P$ is het midden van $MN$. Het snijpunt van $BP$ met $OT$ is $Q$. De schaduwstukken zijn de lijnstukken $MQ$ en $NQ$.

$\left(x,y,z\right)=\left(t,t\mathrm{,3}t\right)$ en $\left(x,y,z\right)=\left(2+2s\mathrm{,2}+2s\mathrm{,3}-3s\right)$.

Er moet gelden: $2+2s=t$ en $3-3s=3t$. Dan $s=\mathrm{‐}1\frac{1}{3}$ en $t=\frac{1}{3}$, dit geeft het punt $Q=\left(1\frac{1}{3}\mathrm{,1}\frac{1}{3}\mathrm{,4}\right)$

$4$

figuur bij opgave 8

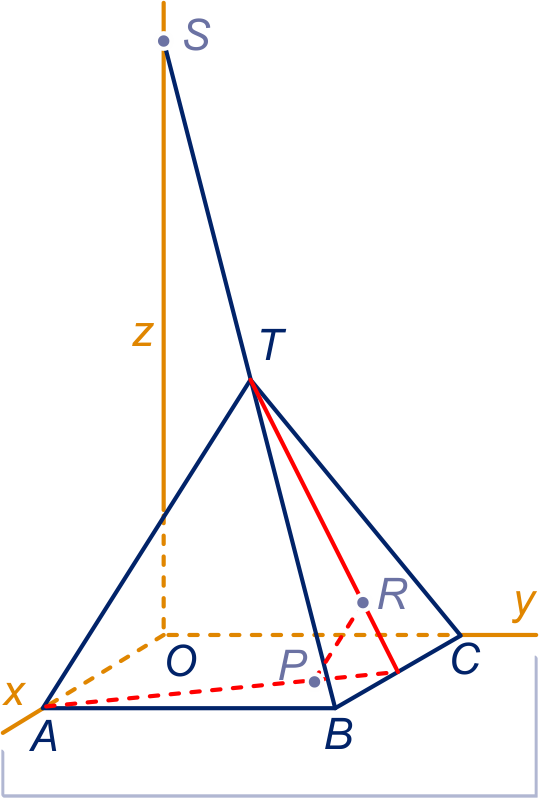
De snijlijn is rood getekend.

Zie figuur. Dit is punt $R$, hierbij zijn de lijnen $AT$ en $PR$ evenwijdig.

Zie figuur: het snijpunt van de $z$-as met lijn $TB$.

Bijvoorbeeld met gelijkvormigheid: $S=\left(\mathrm{0,0,12}\right)$.

-

Jagers: $\left(x,y,z\right)=\left(\mathrm{4,12}-7t,t\right)$, raketten: $\left(x,y,z\right)=\left(8-4s\mathrm{,2}+s,s\right)$. De banen snijden elkaar als er getallen $s$ en $t$ zijn, zó, dat: én $2+s=12-7t$ én $s=t$.
Als je alleen naar de eerste en de derde vergelijking kijkt, vind je: $s=t=1$, maar dan is niet aan de tweede vergelijking voldaan.

Raketten wordt: $\left(x,y,z\right)=\left(8-4s\mathrm{,2}+s,a\cdot s\right)$, waarbij $a$ variabel is. De banen snijden elkaar als er $s$, $t$ en $a$ zijn zó, dat: $8-4s=4$ , $2+s=12-7t$ en $a\cdot s=t$.
Uit de eerste twee vergelijkingen vind je: $s=1$ en $t=1\frac{2}{7}$. Als je dat in de derde vergelijking invult vind je $a=1\frac{2}{7}$, de afvuurrichting is dus: $\left(\begin{array}{c}\mathrm{‐}28\\ 7\\ 9\end{array}\right)$.