Zie figuur 1 .

Zie figuur 2 .

figuur 1 opgave 9

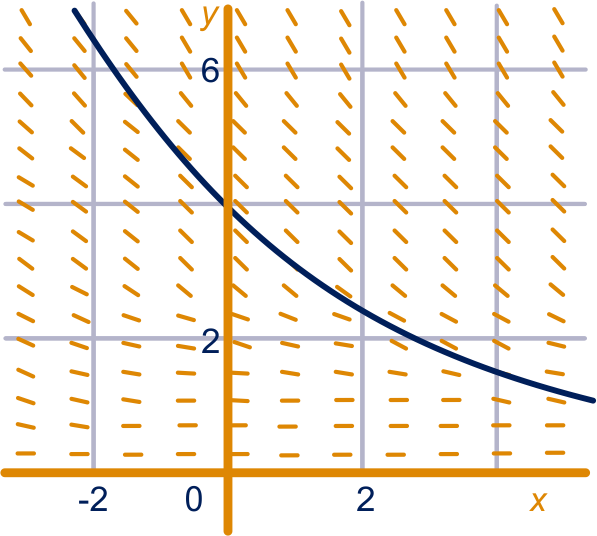
figuur 2 opgave 9

$\frac{\text{d}y}{\text{dx}}=\frac{y}{x}$

Zie figuur .

figuur bij opgave 10

$f(x)=ax$, waarbij $a$ een willekeurig getal is.

Enerzijds geldt voor deze functies $f^{\prime }(x)=a$; anderzijds: $\frac{f(x)}{x}=\frac{ax}{x}=a$. Klopt dus.

De lijnen passen in het richtingsveld.

Enerzijds: in elk punt van de grafiek van $y=\mathrm{‐}x-2$ geldt dat de richtingscoëfficiënt van de raaklijn $\mathrm{‐}1$ is.
Anderzijds: in elk punt van de lijn $y=\mathrm{‐}x-2$ geldt: $\frac{1}{4}{(x+y)}^2-2=\frac{1}{4}{(x+\mathrm{‐}x-2)}^2-2=\mathrm{‐}1$.
Dus in elk punt van de functie $y=\mathrm{‐}x-2$ is de groeisnelheid gelijk aan de door de differentiaalvergelijking voorgeschreven groeisnelheid.

$\frac{1}{4}{(x+y)}^2-2$ is minimaal $\mathrm{‐}2$ als ${(x+y)}^2=0$, dus in alle punten van de lijn $x+y=0$.

-

Cirkels met middelpunt $O(\mathrm{0,0})$.

$x^2+y^2=16\iff y^2=16-x^2\iff y=\pm \sqrt{16-x^2}$. Voor de functie $f$ geldt: $f(x)=\sqrt{16-x^2}$.
$\frac{\text{d}f}{\text{d}x}=\frac{1}{2\sqrt{16-x^2}}\cdot \mathrm{‐}2x=\mathrm{‐}\frac{x}{f(x)}$.
Dus de functie $f$ voldoet aan de differentiaalvergelijking.

$g(x)=\mathrm{‐}\sqrt{16-x^2}$

$\frac{\text{d}g}{\text{d}x}=\mathrm{‐}\frac{1}{2\sqrt{16-x^2}}\cdot \mathrm{‐}2x=\mathrm{‐}\frac{x}{g(x)}$, dus ook de functie $g$ is oplossing van de differentiaalvergelijking.

figuur bij opgave 13

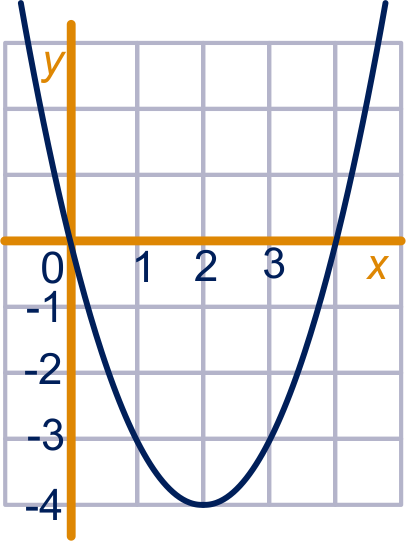
Dat zijn de punten $(x,y)$ met $y-x^2+4x=0$. Die vormen een parabool met top $(\mathrm{2,}\mathrm{‐}4)$.

Dan moet enerzijds $\frac{\text{d}y}{\text{d}x}=$ $2ax+b$.
Anderzijds: $\frac{\text{d}y}{\text{d}x}=y-x^2+4x=a{x}^2+bx+c-x^2+4x=$ $(a-1)x^2+(b+4)x+c$.
Dus voor alle $x$ moet gelden: $2ax+b=(a-1)x^2+(b+4)x+c$, dus dus links en rechts moet dezelfde uitdrukking in $x$ staan. Dus $a-1=0$, $2a=b+4$ en $b=c$. Dit geeft $a=1$, $b=\mathrm{‐}2$ en $c=\mathrm{‐}2$, de functie is dus: $y=x^2-2x-2$.

$\mathrm{0,2}{(x+y)}^2>0$ in elk punt behalve $O(\mathrm{0,0})$, dus elke oplossingsfunctie heeft een positieve helling behalve die door $O$, die heeft daar een horizontale raaklijn.

Op de lijnen met vergelijking $y=\mathrm{‐}x+\sqrt{5}$ en $y=\mathrm{‐}x-\sqrt{5}$;
Op de lijnen met vergelijking $y=\mathrm{‐}x+\sqrt{20}$ en $y=\mathrm{‐}x-\sqrt{20}$

De derde

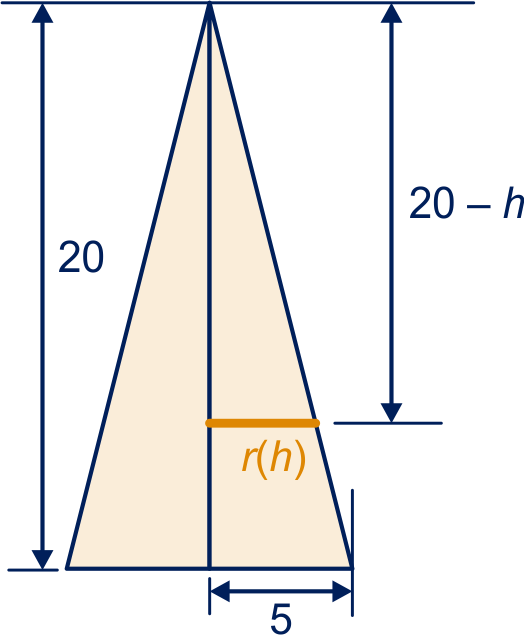
Met gelijkvormigheid volgt: $\frac{r(h)}{5}=\frac{20-h}{20}$, dus $r(h)=5-\frac{1}{4}h$.

$\frac{1}{O(h)}=\frac{1}{\text{π}{(5-\frac{1}{4}h)}^2}=\frac{1}{\frac{1}{16}\text{π}{(20-h)}^2}$, dus $\frac{1}{O(h)}$ is evenredig met $\frac{1}{{(20-h)}^2}$.
En omdat de grafiek dalend is, is de evenredigheidsconstante negatief; vandaar $\mathrm{‐}c$, met $c$ een positief getal.

Enerzijds: $\frac{\text{d}h}{\text{dt}}=\mathrm{‐}\frac{1}{3}{(3ct)}^{\mathrm{‐}\frac{2}{3}}\cdot 3c=\mathrm{‐}c\cdot \frac{1}{{\left(\sqrt[3]{3ct}\right)}^2}$ en anderzijds: $\mathrm{‐}c\cdot \frac{1}{{(20-h)}^2}=\mathrm{‐}c\cdot \frac{1}{{\left(20-\left(20-\sqrt[3]{3ct}\right)\right)}^2}=\mathrm{‐}c\cdot \frac{1}{{\left(\sqrt[3]{3ct}\right)}^2}$.
Dus $h$ is oplossingsfunctie.

$20-\sqrt[3]{3c\cdot 8}=0\iff c=\frac{{20}^3}{8\cdot 3}=333\frac{1}{3}$

Dan $\frac{\text{d}h}{\text{d}t}=\mathrm{‐}2\sqrt{25}=\mathrm{‐}10$, dus met $10$ cm per minuut.

Enerzijds: $\frac{\text{d}h}{\text{d}t}=\mathrm{‐}2(p-t)$.
Anderzijds: $\mathrm{‐}2\sqrt{{(p-t)}^2}=\mathrm{‐}2(p-t)$. Dus de functie $h={(p-t)}^2$ is oplossingsfunctie van de differentiaalvergelijking.

$100={(p-0)}^2$, dus $p=10$.

$h=0\iff {(10-t)}^2=0$, dus na $10$ minuten.