We gaan bewijzen dat de oneindige som
,
dus
gelijk is aan , voor elk getal .
We spreken af ,
dus .
Bijvoorbeeld: .
Bereken , de afgeleide van .
en lijken veel op elkaar.
Deze twee functies verschillen slechts één term, namelijk
.
En als is dat
verschil kleiner dan .
Ga dat na.
Bekijk de functie .
Bereken .
en lijken veel op elkaar.
Deze twee functies verschillen slechts één term, namelijk
.
En als is dat
verschil kleiner dan .
Ga dat na.
Bekijk de eindige som .
Wat is het verschil tussen en ?
Voor elk getal geldt:
De noemer groeit op den duur (veel) sneller dan de
teller .
Daarom wordt het verschil tussen en
voor
grote waarden van zo klein als je maar wil.
Voor de oneindige som
geldt dus: .
En die functies kennen we: , waarbij een
willekeurige constante is.
We moeten nog de waarde van bepalen. Dat lukt
omdat we kunnen uitrekenen.
Wat is de waarde van ?
Uit bovenstaande opgave volgt:
In het vervolg bekijken we hoe je voor
zonder
haakjes schrijft.
Een afleiding met haakjes wegwerken
Schrijf voor en met zo weinig mogelijk termen zonder haakjes.
Hoe gaat dit verder? Zit er enig systeem in? Wat zal opleveren? We gaan dat op verschillende manieren aanpakken.
Eerst bekijken we hoe we de haakjes in wegwerken.
We gaan de haakjes in wegwerken.
Als je de haakjes wegwerkt, krijg je een veelterm van graad ,
dus een som van de vorm:
.
Om hier beter over te kunnen praten geven we de coëfficiënten (de getallen op de puntjes) namen:
.
Je weet waarschijnlijk bij voorbaat wel wat
en zijn
Wat zijn die?
Stel dat je de uitwerking van kent. Dan volgt daaruit de uitwerking van als volgt.
.
Dus:
Als je dus de coëfficiënten van de uitwerking van kent, ken je die ook van de uitwerking van
: je moet gewoon steeds twee opvolgende coëfficiënten van de uitwerking van
optellen.
Om aan de uitwerking van te komen, moet je het schema invullen.
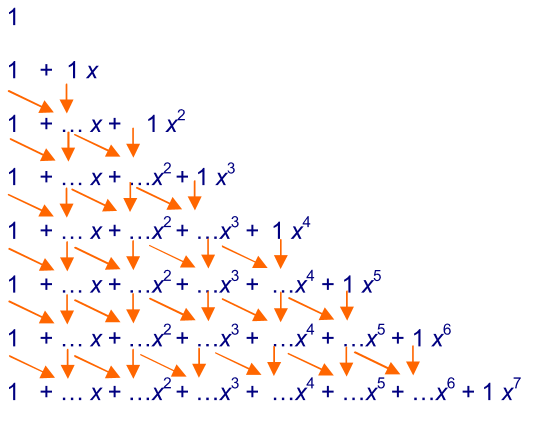
Vul de coëfficiënten op het werkblad van bovenaf in.
Dit schema is een oude bekende. Met precies hetzelfde schema maak je namelijk de driehoek van Pascal.
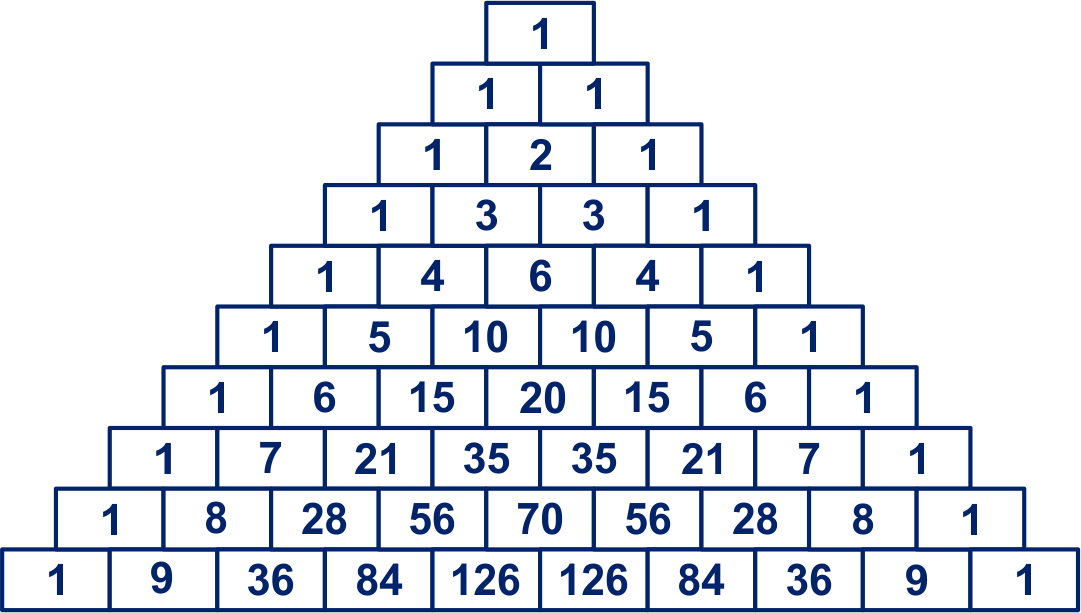
Kennelijk is de coëfficiënt van bijvoorbeeld in de uitwerking van gelijk aan .
Wat is de coëfficiënt van in de uitwerking van ?
Uit bovenstaande volgt:
.
In de -notatie: .
We hebben nog geen uitwerking voor .
Deze volgt uit de formule hierboven als volgt.
.
Bekijk .
We gaan linker- en rechterlid vier keer differentiëren.
De vierde afgeleide van het linkerlid is .
Schrijf de vierde afgeleide van het rechterlid op.
Nu vullen we voor in beide vierde afgeleides in en vereenvoudigen de uitkomsten.
Wat zijn die uitkomsten?
Hieruit volgt: .
Ga dat na.
Wat je in opgave 4 gedaan hebt, kun je algemeen uitvoeren. De coëfficiënt van in vind je door beide leden van keer te differentiëren en vervolgens voor in te vullen.
Een afleiding met kansrekening
We bekijken het asymmetrische Galtonbord met 10 rijen. Voor een kogeltje is de kans om naar links te vallen en de kans om naar rechts te vallen . We nummeren de bakjes van links naar rechts: 0, 1, 2, …, 10.
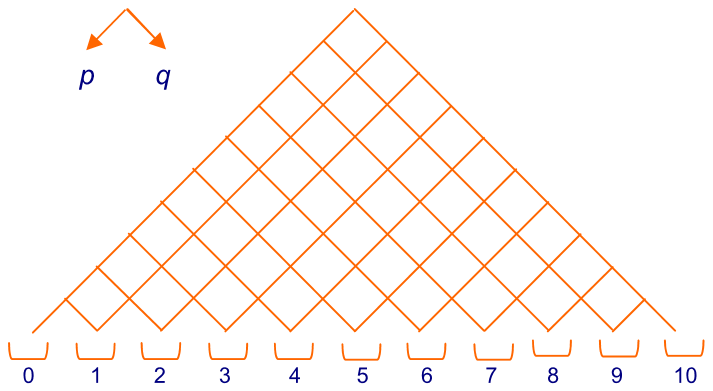
Wat is de kans dat een kogeltje in bakje met nummer terecht komt?
Leg uit: .
Als je beide leden van de formule in onderdeel b vermenigvuldigt met krijg je:
.
Leg dat uit.
Vervang door en door . Dan krijg je :
.
Leg dat uit.
Voor alle getallen en en
alle positieve gehele getallen geldt:
.
Deze formule staat bekend als het binomium van Newton.
is een tweeterm (binomus); vandaar de naam.
Schrijf zonder haakjes, zo eenvoudig mogelijk.
Laat met het binomium van Newton zien dat .
