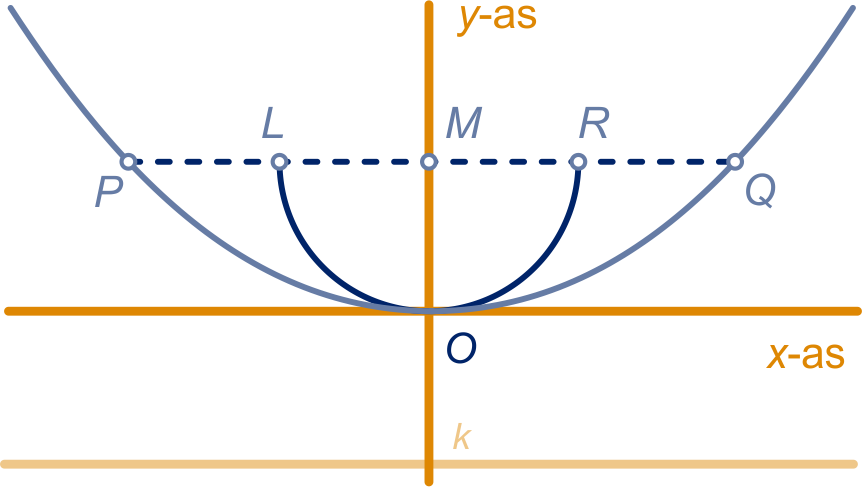
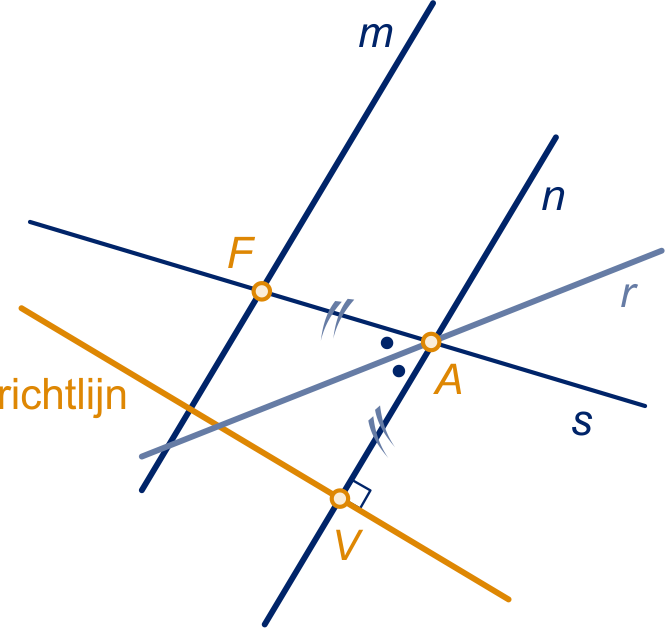
Het stuk 'links' van heeft als richtlijn de
-as en brandpunt ,
het stuk tussen en heeft als
richtlijn met vergelijking
en brandpunt ,
het stuk 'rechts' van heeft
als richtlijn de -as en
brandpunt .
De overgangspunten en
liggen op de lijn door en
en liggen even ver van
als van .
Dus en
.
(Dan ligt ook even ver van de
-as en en
even ver van de
-as en .)
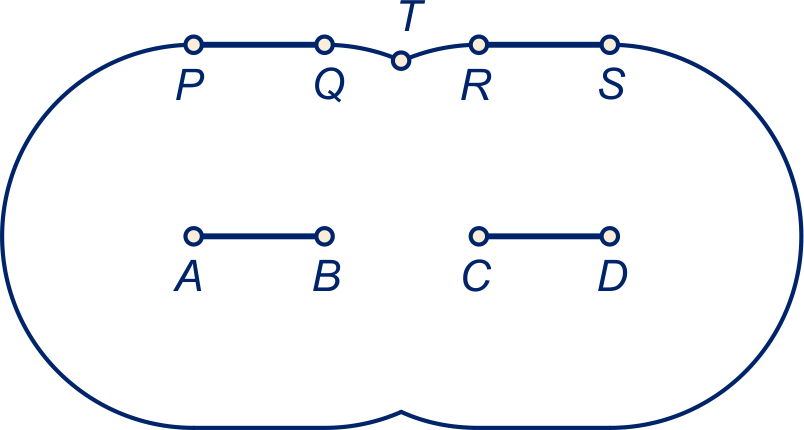
Alle zijden van driehoek hebben
lengte , dus boog
heeft lengte
.
De lengte van de isolijn is dus:
.
, dus de raaklijn heeft vergelijking
voor zekere waarde van
.
ligt op de raaklijn, dus
en de vergelijking is:
.
Voor het snijpunt met de -as geldt:
.
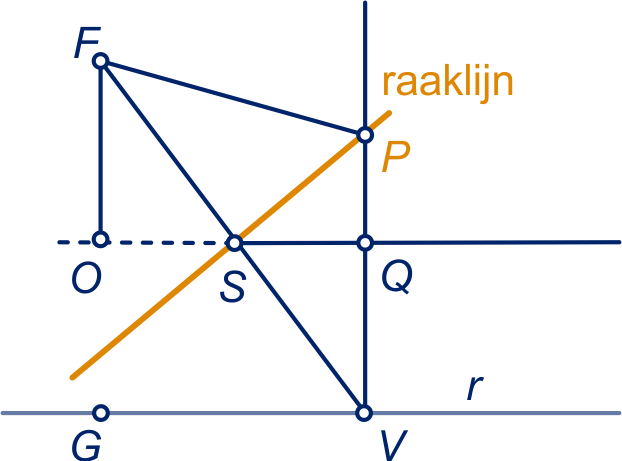
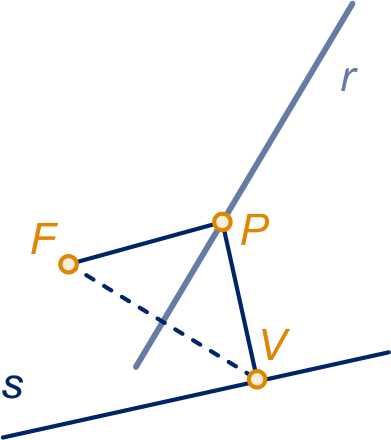
is het voetpunt van
op de richtlijn
en
het voetpunt van .
Het snijpunt van de raaklijn in en
lijn noemen we .
De lijn door evenwijdig met de richtlijn gaat door
omdat
het midden van lijnstuk
is en
het midden van lijnstuk
.
Dus !
De driehoeken en
zijn
congruent (HZH), dus is het midden van
lijnstuk .
Zie figuur 1 aan het einde van de opgave.
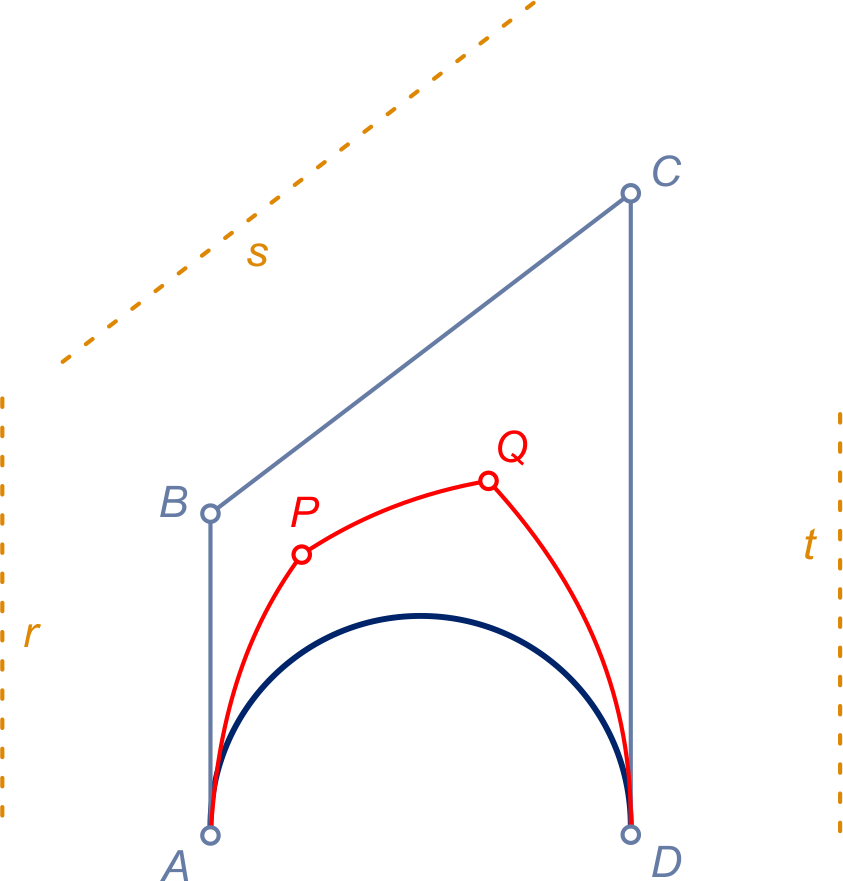
De conflictlijn bestaat uit twee stukken parabool. Beide hebben brandpunt . Het 'bovenste' stuk heeft richtlijn , het 'onderste' stuk heeft richtlijn , beide op afstand op afstand van .
Zie figuur 2 hieronder.
De gevraagde hoek is hetzelfde als hoek .
De projectie van op
noemen we .
Uit de stelling van Pythagoras in driehoek
volgt: , dus
.
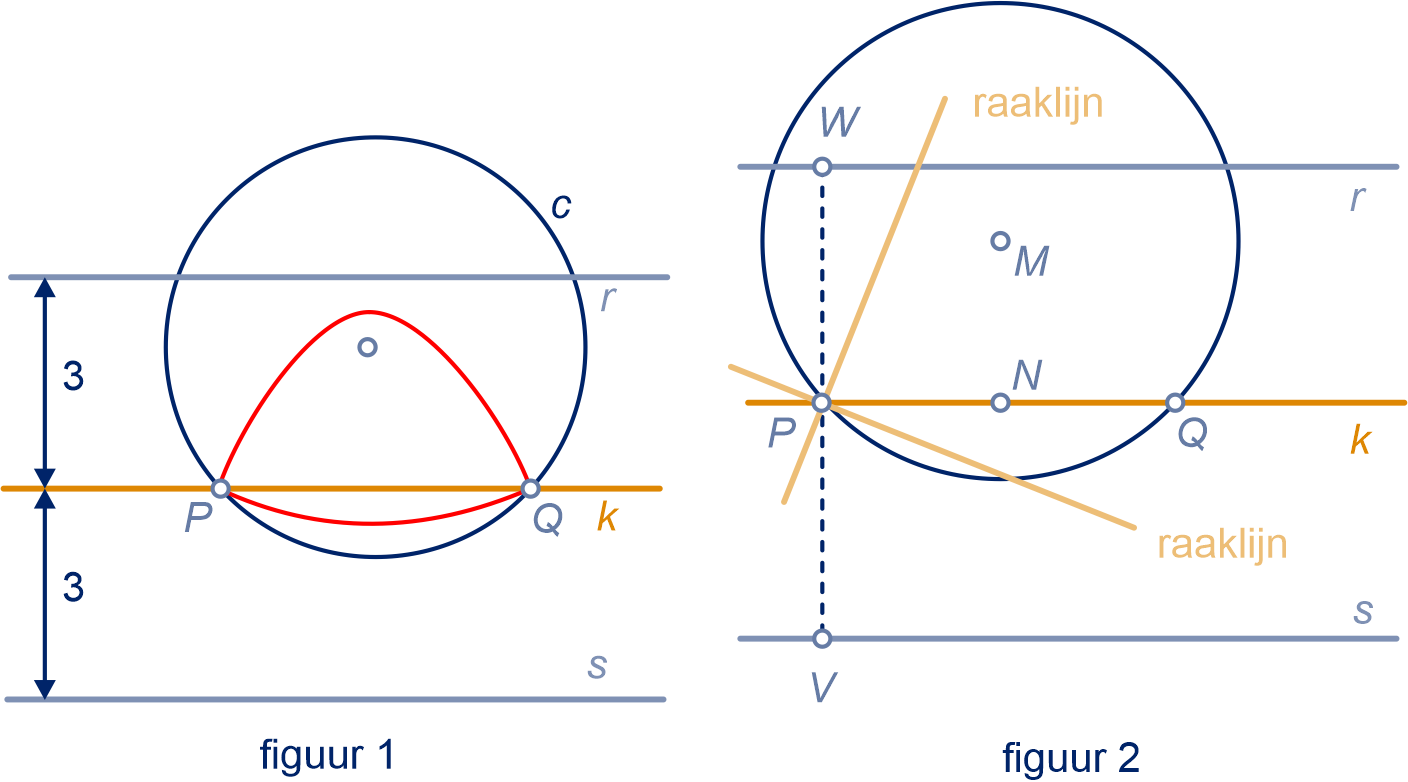
Teken de lijn door evenwijdig aan de as
. Hierop moet het voetpunt
van liggen.
Spiegel de lijn in de raaklijn
, het beeld is . Op ligt het brandpunt.
Het brandpunt is dus het snijpunt van de as
met .
vind je met de eigenschap .
De richtlijn gaat door en staat loodrecht
op de as .
Spiegel in . Het beeld is het voetpunt van . De loodlijn in op lijn is de richtlijn.
De richtlijnen zijn
,
en
op afstand
van
,
en
.
Het brandpunt is steeds
Stel , dan
.
Lijn is bissectrice
van hoek en
lijn van hoek
, dus
en
.
De afstand tot land I noemen we , dan is de afstand tot land III ook en tot land II: , dus . dus .
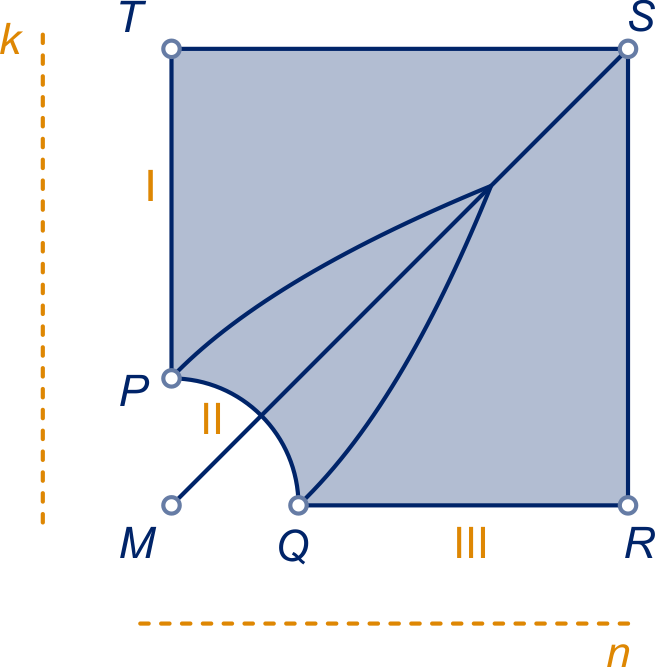
Eén stuk is een gedeelte van de parabool met brandpunt en richtlijn ,
een lijn die eenheden
links van lijn .
- de parabool gaat door punt ;
- het tweede stuk is een gedeelte van de bissectrice van hoek ;
- het derde stuk is het spiegelbeeld van het eerste stuk (of een gedeelte van de parabool met
brandpunt en richtlijn , een lijn die
eenheden onder lijn ligt.
Het voetpunt van op
noemen we en het snijpunt van
lijn met
zijde : .
De raaklijn aan het bovenstuk is deelt hoek doormidden. Dus vanwege symmetrie is de gevraagde hoek even groot als hoek
.
In driehoek geldt:
en
. Noem de gevraagde hoek
, dan
,
de gevraagde hoek is dus exact!
