Congruent

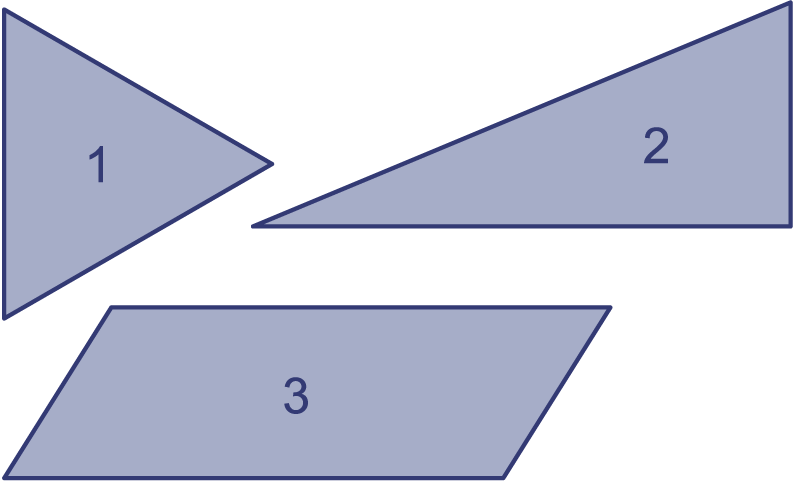
De gelijkzijdige driehoek, rechthoekige driehoek en parallellogram staan ook op het knipblad.

Snij ze uit. Zorg ervoor dat de openingen waar je ze uit haalt, heel blijven.
Ga voor elke figuur na op hoeveel manieren hij in zijn opening past. Maak daarbij onderscheid tussen niet ondersteboven en wel ondersteboven. Noteer je antwoorden in een tabel:

figuur	1	2	3
ondersteboven
niet-ondersteboven
symmetrieassen?	ja

Beantwoord ook de vraag of de figuur (één of meer) symmetrieassen heeft.

Als een figuur een symmetrieas heeft, past hij ook ondersteboven in zijn opening. Anders niet.

Een spiegelsymmetrische figuur kun je namelijk om zijn symmetrieas ondersteboven draaien zonder dat hij van plaats verandert.

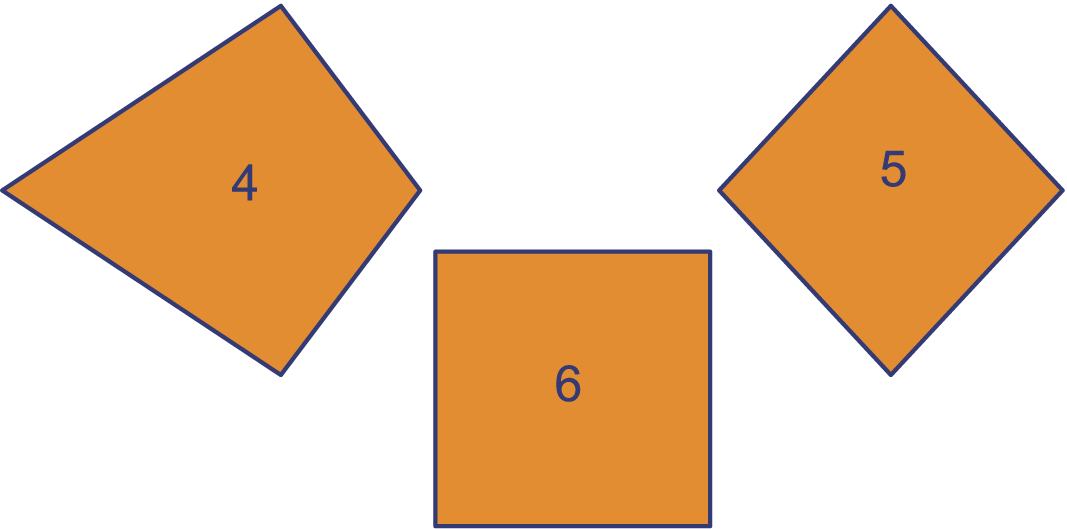
De vlieger, ruit, en vierkant staan ook op het knipblad.
Snij de figuren weer uit.

Hoe vaak past de figuur in zijn eigen opening? Schrijf je antwoorden in een tabel:

figuur	4	5	6
ondersteboven
niet-ondersteboven
symmetrieassen?	ja

Wat heeft de orde van draaisymmetrie te maken met het aantal malen dat de figuur niet ondersteboven in zijn opening past?

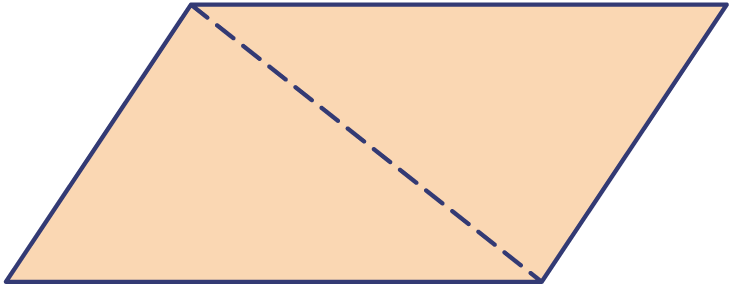
Teken een parallellogram op een kladblaadje en knip het uit. Verdeel het in twee driehoeken door langs een diagonaal te knippen.

De twee driehoeken passen precies op elkaar; we zeggen dat ze congruent zijn.

De figuren A1 en A2 zijn congruent: ze kunnen elkaar precies bedekken. De figuren B1 en B2 kunnen elkaar ook precies bedekken, maar daarvoor moet je eerst één van beide ondersteboven leggen. We noemen B1 en B2 indirect congruent, in tegenstelling tot A1 en A2, die we direct congruent noemen.

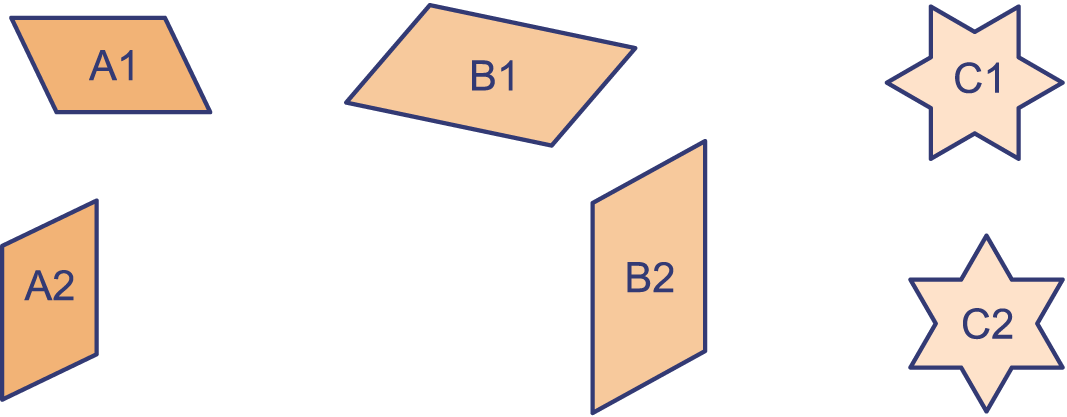
Zijn C1 en C2 direct of indirect congruent?

Drie keer twee congruente figuren: twee handen, twee munten en twee vlekken.

Welke zijn direct en welke indirect congruent?

Verdeel de vier figuren in twee congruente helften.

(hint)

Tip: Teken de figuren over op vierkantjes- of driehoekjespapier.

Puntsymmetrie

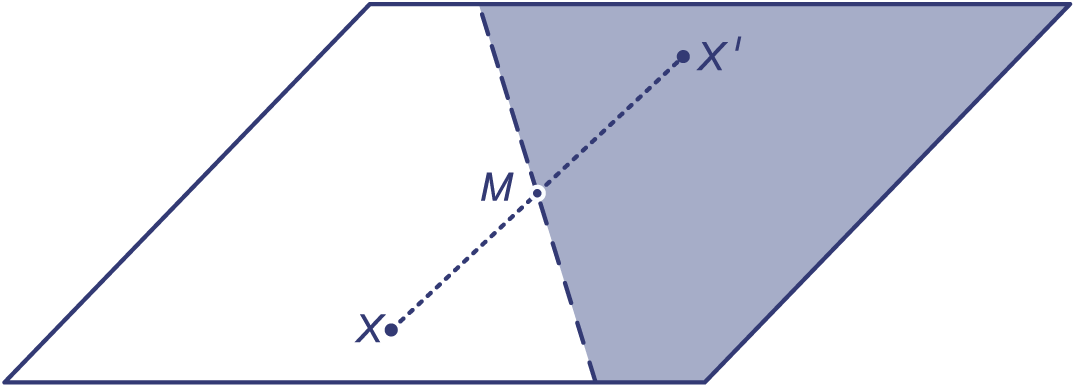
Over het parallellogram is nog iets meer te vertellen. Ook als je het niet langs een diagonaal, maar langs een willekeurige lijn door het middelpunt $M$ in tweeën knipt, zijn de helften indirect congruent.

Kies een punt $X$ in de ene helft. Zoek het daarmee corresponderende punt $X'$ in de andere helft. Dan is $M$ altijd het midden van lijnstuk $X X'$ . Je kunt ook zeggen dat $X$ en $X'$ elkaars spiegelbeeld zijn $i n$ het punt M.

Teken een gelijkzijdige driehoek $A B C$ en zoek het middelpunt $M$ op.

Teken het spiegelbeeld $A'$ van $A$ in $M$ ; dat wil zeggen, bepaal $A'$ zo dat $M$ het midden is van $A A'$ .

Teken ook de spiegelbeelden $B'$ en $C'$ in $M$ .

Teken vervolgens driehoek $A' B' C'$ . Dit is het spiegelbeeld van driehoek $A B C$ in $M$ .

De totale figuur (het parallellogram) die bestaat uit de twee driehoeken is puntsymmetrisch. $M$ heet het symmetriepunt.

Teken een lijnstuk $A B$ van 4 cm. Teken op $A B$ een halve cirkel. $M$ is het punt op $A B$ , op 1 cm afstand van $B$ .

Teken het spiegelbeeld van de halve cirkel in $M$ .

De totale figuur die bestaat uit de twee halve cirkels is puntsymmetrisch, met $M$ als symmetriepunt.

Een figuur heet puntsymmetrisch als hij uit twee helften bestaat die elkaars spiegelbeeld zijn in een punt.

Dat punt is het symmetriepunt van de figuur.

Elke puntsymmetrische figuur is draaisymmetrisch.

Wat is het draaipunt?

Van welk orde?

Welke logo's van opgave 6 (zie hiernaast) zijn puntsymmetrisch?

Welke soorten bijzondere vierhoeken zijn puntsymmetrisch?

Is elke draaisymmetrische figuur ook puntsymmetrisch? Geef een voorbeeld.

Een zekere draaisymmetische figuur is ook puntsymmetrisch.

Wat weet je van zijn orde van draaisymmetrie.

Rozetten

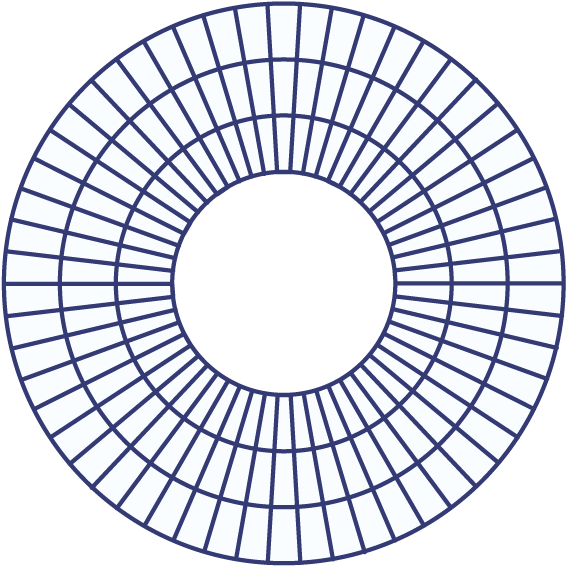
Een rozet is een cirkelvormig patroon met draaisymmetrie. Er kunnen ook spiegelassen bij optreden.

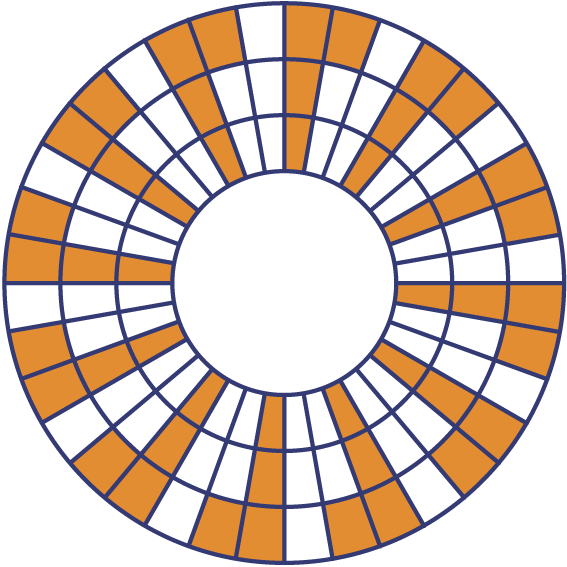
De ringen in de figuur zijn in 36 vakjes verdeeld.

Door sommige vakjes oker te kleuren is een rozet gemaakt: een draaisymmetrisch patroon.

Van welke draaiorde is dit patroon?

Kleur op het werkblad de vakjes zó, dat een patroon van orde 9 ontstaat.

Kun je door vakjes te kleuren een patroon van orde 5 krijgen?

En een patroon van orde 6?

10s

11s

De cirkelringen zijn verdeeld in 54 vakjes. Je kunt hierin rozetten tekenen door vakjes in te kleuren.

Van welke orde kunnen die rozetten zijn?

Dezelfde vraag als de cirkelringen verdeeld zijn in 35 vakjes.

Hieronder zie je de twaalf vormen die je kunt maken door 5 vierkantjes tegen elkaar te leggen (je mag ze ook omdraaien). Dit zijn de twaalf pentomino's.
De twaalf vormen hebben een naam gekregen in de vorm van een letter. Je snapt bij elk stukje wel waarom die naam is gekozen.

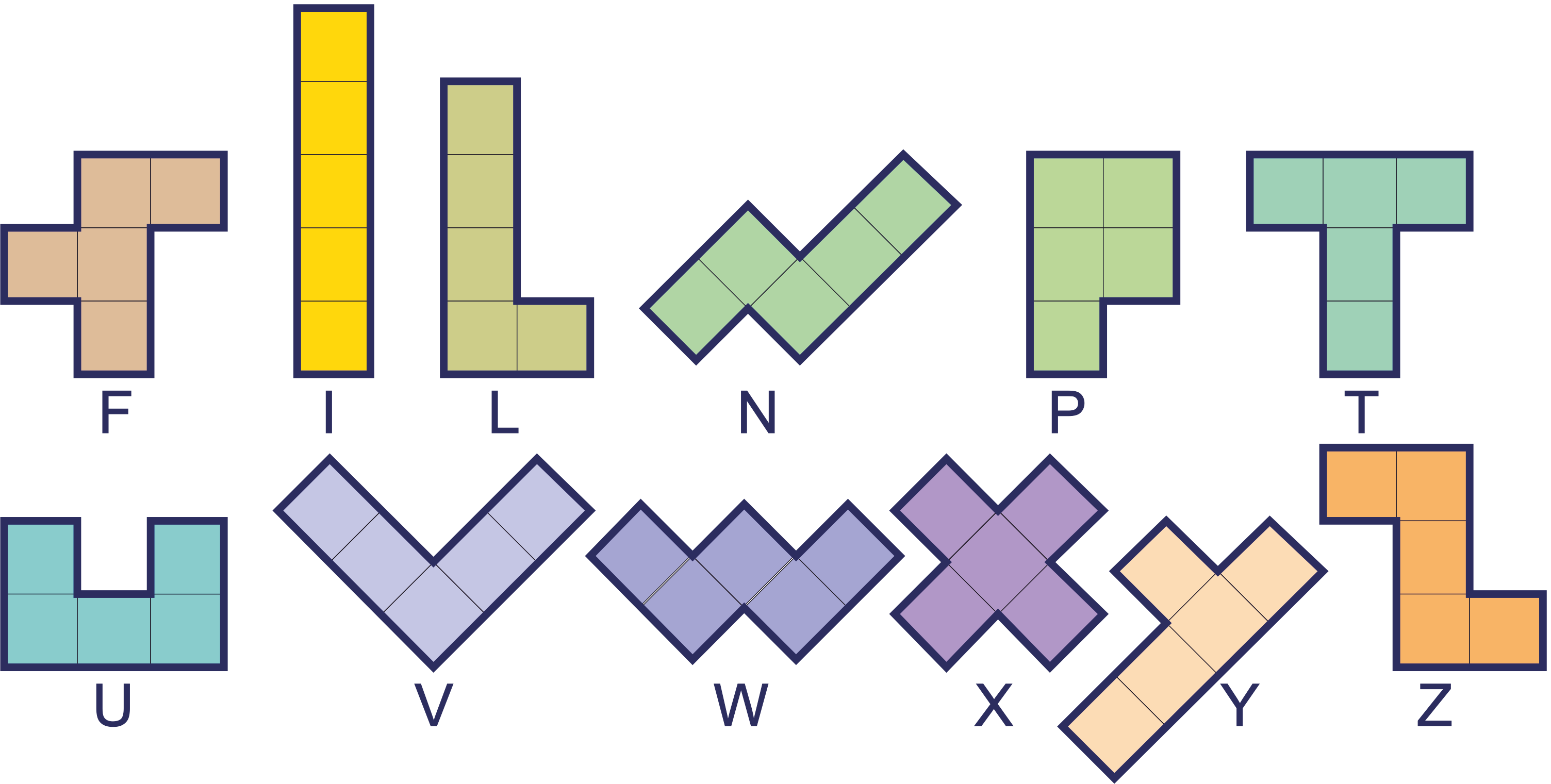
Welke van de twaalf puzzelstukjes zijn lijnsymmetrisch? Vermeld ook het aantal symmetrieassen.

Welke van de twaalf puzzelstukjes zijn draaisymmetrisch? Vermeld ook de draaiorde.

Welke van de twaalf puzzelstukjes zijn puntsymmetrisch?