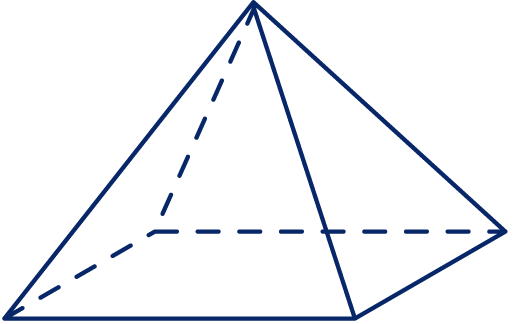
15.4 Rekenen aan gelijkvormige figuren >

Zoveel keer zo groot

Een piramide heeft een grondvlak van 4 bij 4. De top ligt midden boven het grondvlak op hoogte 3. We bekijken piramides die gelijkvormig zijn met deze piramide.

Wat is de hoogte als het grondvlak 8 bij 8 meet?

En als het grondvlak 10 bij 10 meet?

Wat zijn de afmetingen van het grondvlak als de hoogte 4,5 is?

En als de hoogte 2 is?

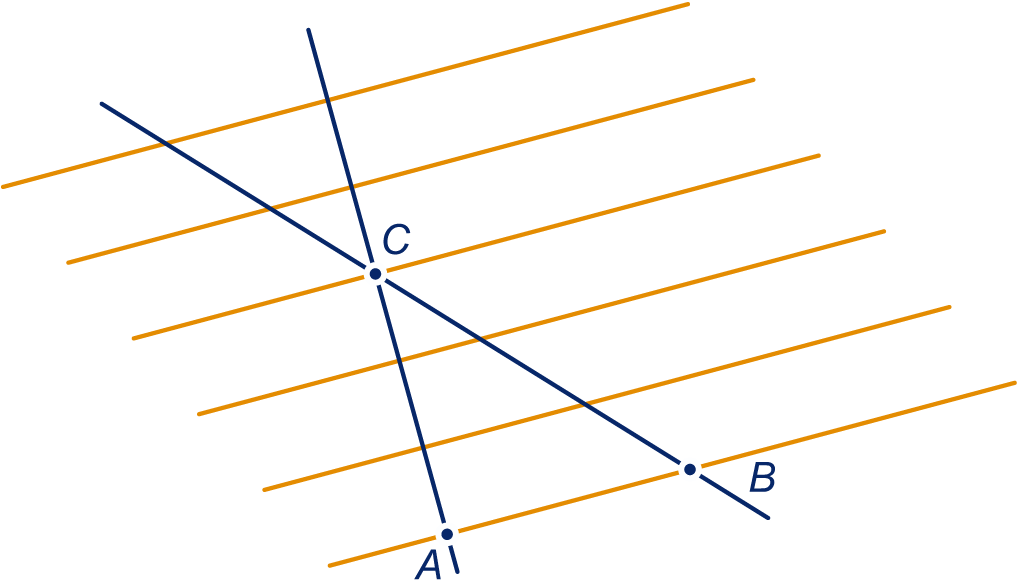
figuur 1

figuur 2

De zes lijnen in figuur 1 zijn evenwijdig en hebben opvolgend gelijke afstanden.
$A$ en $B$ liggen op een van de lijnen en punt $C$ op een andere.
Verder zijn de twee lijnen $A C$ en $B C$ getekend.

Hoeveel driehoeken zijn in de figuur ontstaan?

We tekenen de driehoeken even apart (zie figuur 2).

Hoe weet je zeker dat de driehoeken gelijkvormig zijn?

Van de grootste driehoek zijn de zijden 8, 9 en 12.

Wat zijn de zijden van de andere driehoeken. Schrijf je antwoorden bij de zijden op het werkblad.

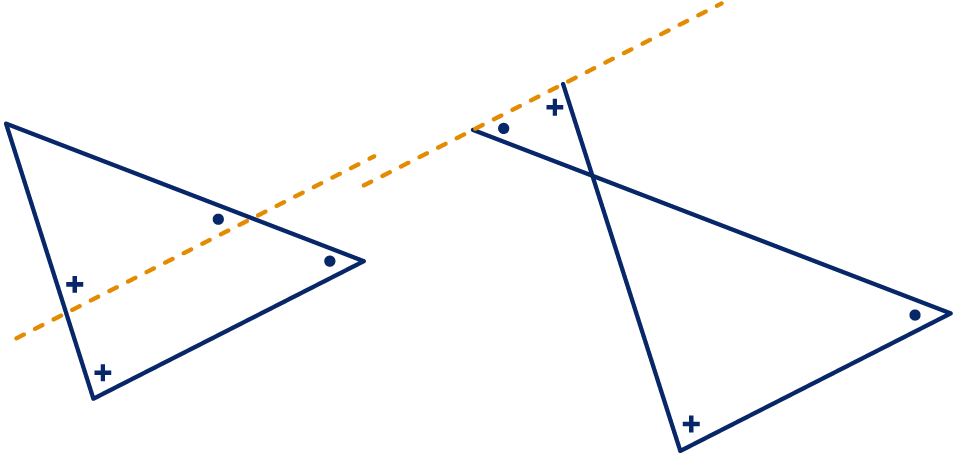
Als bij een driehoek een lijn evenwijdig is aan een van de zijden, snijdt die van de driehoek een stuk af dat gelijkvormig is met de hele driehoek. Net zo iets is aan de hand als de lijn buiten de driehoek wordt getekend, evenwijdig aan een zijde. Dan moet je de andere twee zijden verlengen.

Dat de kleine driehoek gelijkvormig is met de grote komt doordat ze gelijke hoeken hebben; dat is met tekens aangegeven.

figuur 1

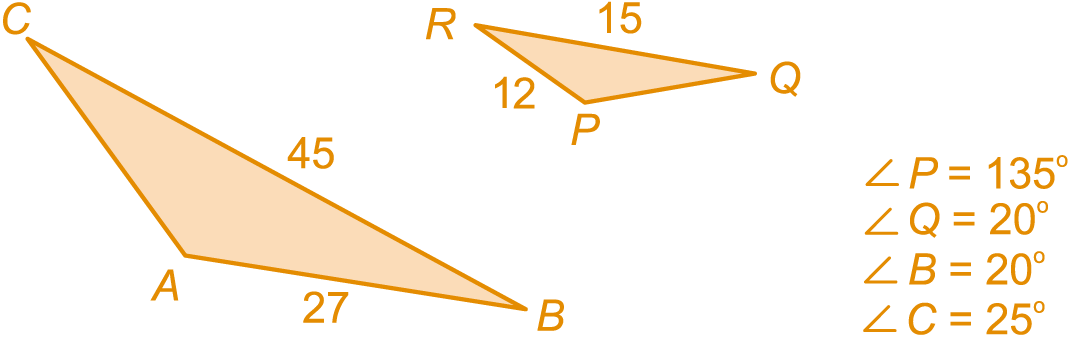
Van de driehoeken $A B C$ en $P Q R$ zijn de hoeken $P$ , $Q$ , $B$ en $C$ gegeven.

Waarom zijn deze driehoeken gelijkvormig?

Wat is de factor van de grote naar de kleine driehoek?

Bereken de lengte van zijde $P Q$ .

Bereken ook de lengte van $A C$ .

figuur 2

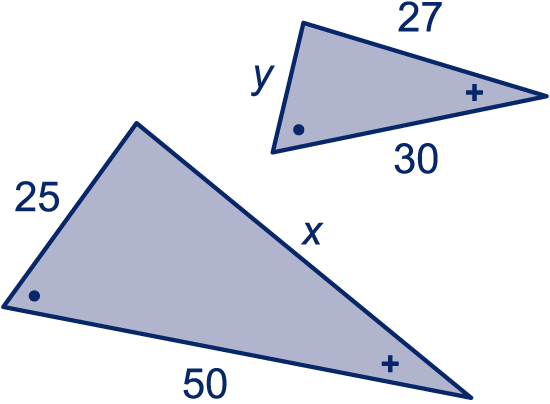
De blauwe driehoeken zijn ook gelijkvormig.

Bereken $x$ en $y$ .

Het verkeersbord is 2 meter hoog en zijn schaduw 3 meter lang.
De lantaarnpaal is 7 meter hoog. De boom heeft een schaduw van 21 meter.

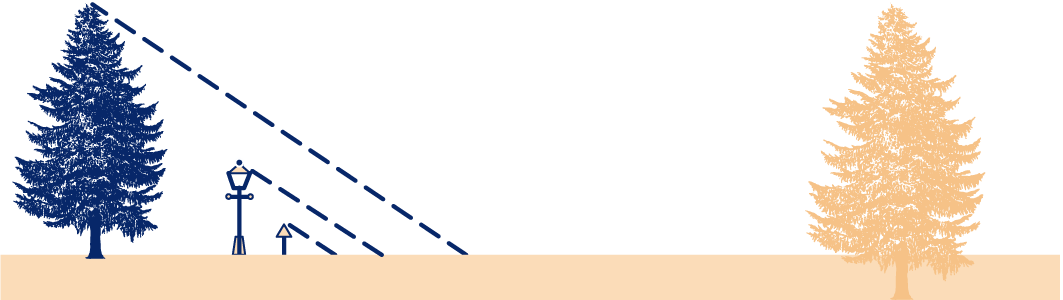
Hoe hoog is de boom?

Hoe lang is de schaduw van de lantaarnpaal?

Waarschijnlijk heb je in de vorige opgave steeds een factor berekend van het ene naar het andere object. Zo was de factor van het verkeersbord naar de boom 7 en de factor van het verkeersbord naar de lantaarnpaal $3 \frac{1}{2}$ . Je kunt het ook anders bekijken. De schaduw van het verkeersbord is $1 \frac{1}{2}$ maal zo lang als de hoogte of de hoogte is $\frac{2}{3}$ van de schaduw. Dan moet dat ook bij de boom en lantaarnpaal gelden.

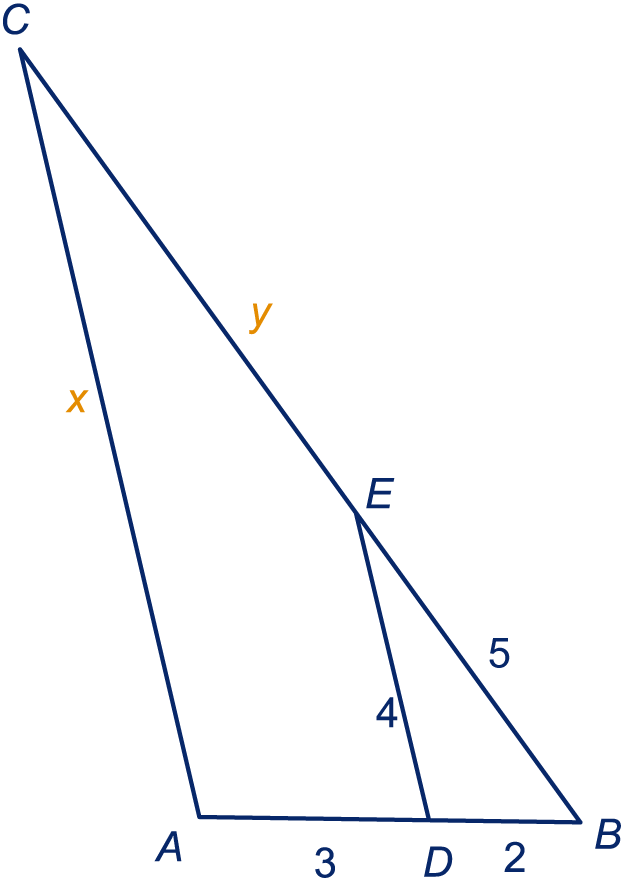
De hoogte van de boom kun je dan ook uitrekenen door $\frac{2}{3} \cdot 21 = 14$ (of $21 : 1 \frac{1}{2} = 14$ ) te doen en de lengte van de schaduw van de lantaarnpaal door $7 \cdot 1 \frac{1}{2} = 10 \frac{1}{2}$ (of $7 : \frac{2}{3} = 10 \frac{1}{2}$ ) te doen.

De lijnen $A C$ en $D E$ zijn evenwijdig. De andere gegevens staan in de figuur.

Teken de driehoeken $A B C$ en $D B E$ naast elkaar. Schrijf de letters bij de hoekpunten en de lengtes bij de zijden.

Bereken $x$ .

Bereken $y$ .

Gespiegeld gelijkvormig

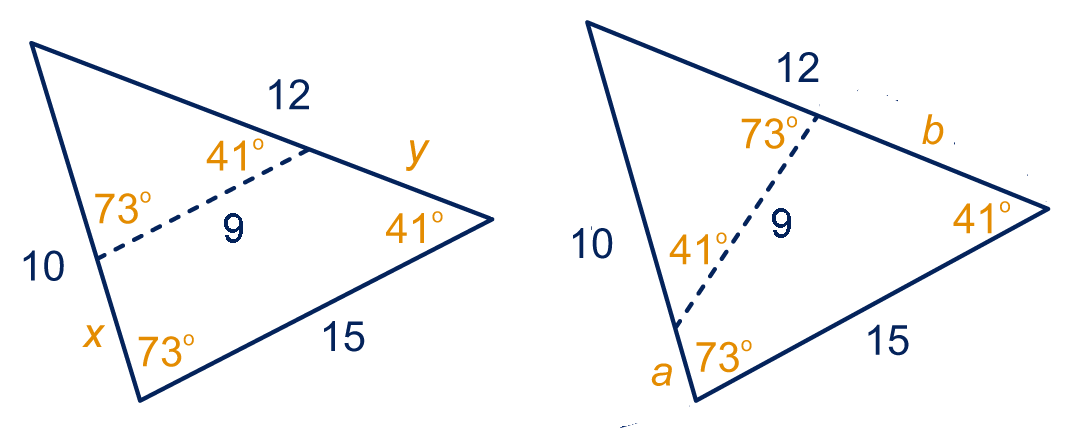
Voor gelijkvormigheid hoeft de stippellijn op de vorige bladzijde niet per se evenwijdig aan een zijde te lopen: hij kan ook anti-evenwijdig lopen. We geven een voorbeeld.

Links loopt de stippellijn evenwijdig aan een zijde, rechts is hij anti-evenwijdig met die zijde. Bij anti-evenwijdig is de kleine driehoek spiegelgelijkvormig met de hele driehoek.

De zijden van de grote driehoeken zijn 10, 12 en 15. Beide stippellijn hebben lengte 9.

Hoe lang zijn de twee andere zijden van beide kleine driehoeken?

Hoe lang zijn de stukken $x$ en $y$ in de linker figuur?

En de stukken $a$ en $b$ in de rechter figuur?

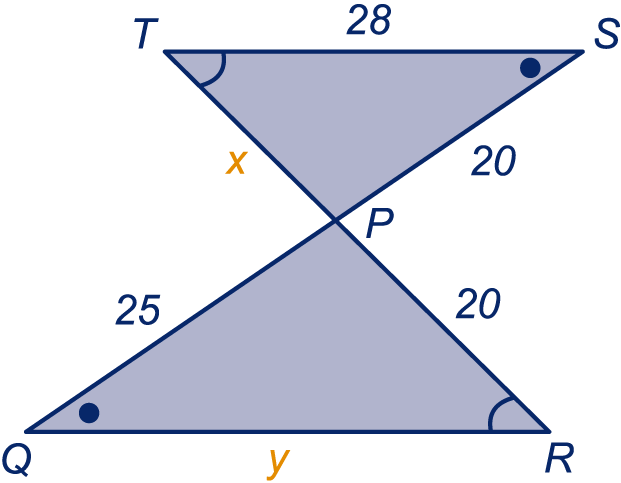
$S T$ is evenwijdig aan $Q R$ . De overige gegevens staan in de tekening.

Wat is de factor van driehoek $P S T$ naar driehoek $P Q R$ ?

Bereken $x$ en $y$ .

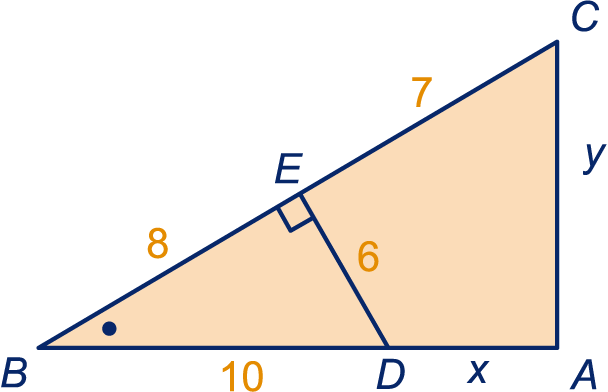
De hoeken $E$ en $A$ zijn recht. De overige gegevens staan in de tekening.

Waarom zijn de driehoeken $B D E$ en $B C A$ gelijkvormig?

Wat is de factor van driehoek $B E D$ naar driehoek $B A C$ ?

(hint)

Kijk naar de schuine zijden van de driehoeken.

Bereken $x$ en $y$ .

Door elkaar

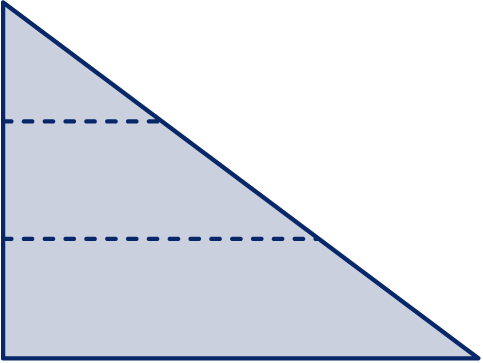
Getekend is een driehoek met zijden 3, 4 en 5. De stippellijnen verdelen de verticale zijde in drie stukken van lengte 1.

Hoe lang zijn de stukken waarin de schuine zijde verdeeld wordt?

Hoe lang zijn de stippellijnen?

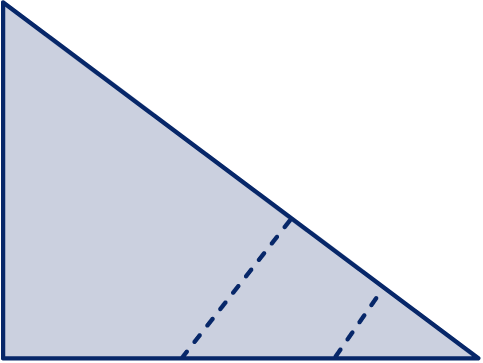
We bekijken opnieuw de driehoek met zijden 3, 4 en 5.
De stippellijnen staan nu loodrecht op de schuine zijde. Ze verdelen de schuine zijde in stukken van lengte 3, 1 en 1.

Hoe lang zijn de stukken waarin de horizontale zijde verdeeld wordt?

Hoe lang zijn de stippellijnen?

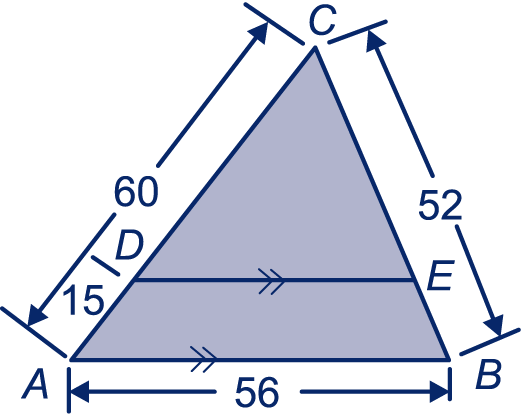
Van driehoek $A B C$ is gegeven: $A B = 56$ , $B C = 52$ en $C A = 60$ . Het punt $D$ verdeelt zijde $A C$ in stukken van 15 en 45.
Het punt $E$ ligt op zijde $B C$ , zó dat $D E$ evenwijdig is aan $A B$ .

Wat is de factor van de grote naar de kleine driehoek?

Bereken $D E$ en $C E$ .

12s

Getekend is een driehoek met zijden 2, 3 en 4 cm.

Er zijn drie driehoeken die gelijkvormig zijn met deze driehoek en die een zijde van 6 cm hebben.
Teken ze alle drie. Schrijf bij elke zijde hoe lang die is.

10s

13s

figuur 1

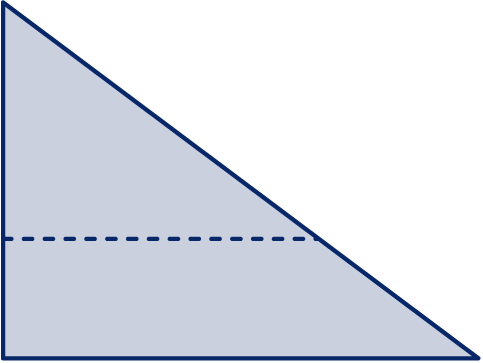
In figuur 1 staat een driehoek met zijden 3, 4 en 5.

De stippellijn verdeeld de verticale zijde in stukken van lengte $a$ en $3 - a$ ; het bovenste stuk heeft lengte $a$ .

Hoe lang zijn de stukken waarin de schuine zijde verdeeld wordt? Druk je antwoorden uit in $a$ .

Hoe lang is de stippellijn? Druk je antwoord uit in $a$ .

figuur 2

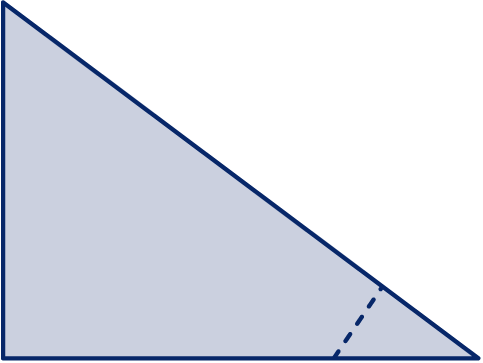
In figuur 2 staat weer een driehoek met zijden 3, 4 en 5. De stippellijn staat loodrecht op de schuine zijde.

Hij verdeelt de schuine zijde in stukken van lengte $a$ en $5 - a$ ; het onderste stuk heeft lengte $a$ .

Hoe lang zijn de stukken waarin de stippellijn de horizontale zijde verdeeld? Druk je antwoorden uit in $a$ .

Hoe lang is de stippellijn? Druk je antwoord uit in $a$ .

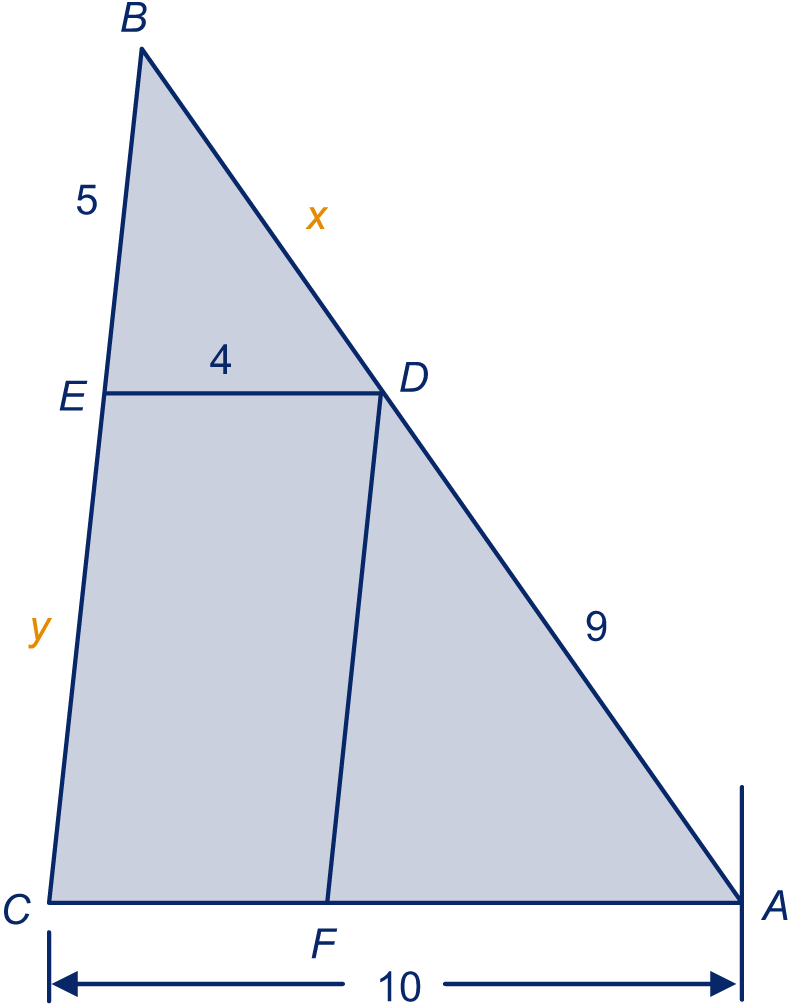
In driehoek $A B C$ is $E D F C$ een parallellogram. De overige gegevens staan in de tekening.

Wat is de factor van driehoek $B E D$ naar driehoek $B C A$ ?
En wat is de factor van driehoek $B E D$ naar driehoek $D F A$ ?

Bereken $x$ en $y$ .