Omdat en (-hoeken); gelijkvormigheidskenmerk .
De gelijkvormigheidsfactor van driehoek naar driehoek is 2 (dat zie je aan de zijden en ). Dus is de hoogte van driehoek ook 2 keer zo groot als die van driehoek . Omdat de hoogtes samen 3 zijn, zijn de hoogtes afzonderlijk 2 en 1.
opp. en opp.
De oppervlakte van de driehoeken en is . Trek daar de oppervlakte van driehoek vanaf en je vindt de oppervlakte van de driehoeken en : .
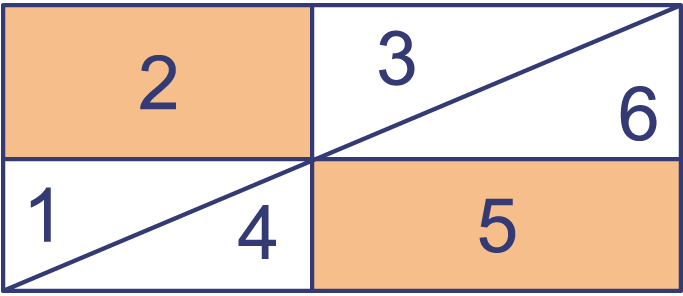
De stukken 1, 2 en 3 samen zijn even groot als de stukken 4, 5 en 6 samen.
De stukken 1 en 4 zijn even groot en de stukken 3 en 6 zijn even groot.
Dus zijn de stukken 2 en 5 ook even groot.
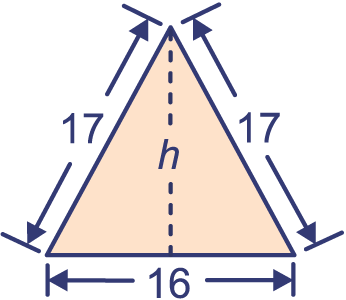
Teken de hoogtelijn en bereken de hoogte van de driehoek met de stelling van Pythagoras.
Oppervlakte driehoek =
opp. parallellogram = ; opp. driehoek = .
Dus is de oppervlakte van het trapezium .
opp ene driehoek = ; opp. andere driehoek = .
Dus is de oppervlakte van het trapezium .
Het parallellogram heeft basis en heeft oppervlakte .
Het trapezium is de helft daarvan en heeft dus oppervlakte .
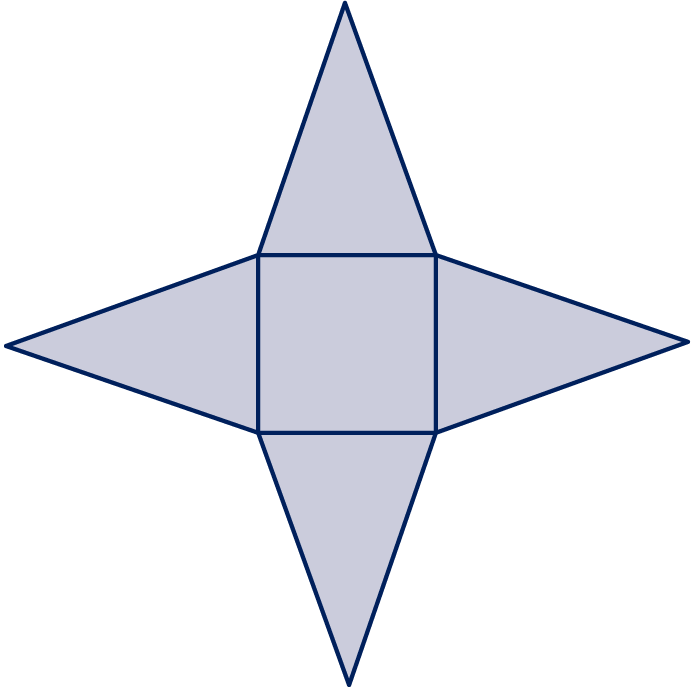
We berekenen eerst de hoogte van een driehoekig zijvlak met de stelling van Pythagoras.
, dus cm.
opp. driehoekig zijvlak =
de totale oppervlakte van het karton is cm2.
Driehoek is even hoog als driehoek , maar heeft een 2 keer zo grote basis, dus een 2 keer zo grote oppervlakte. Die is dus 42.
Driehoek is even hoog als driehoek , maar de bases verhouden zich als 4 : 3. Hun oppervlaktes verhouden zich dus ook als 4 : 3. Dus is driehoek driezevende deel van driehoek . Zijn oppervlakte is dus .
De oppervlakte van het rechter parallellogram is keer zo grote oppervlakte. De oppervlaktes verhouden zich dus als 3 : 1.
, .
.
De twee witte driehoeken vormen een rechthoek van 5 bij 1,5. Door deze en het kleine vierkant van het grote vierkant weg te halen, houd je de oker pijl over. Zijn oppervlakte is: .
De trapezia hebben hoogte 3. Hun oppervlakte is . Dit is één derde van het hele vierkant.
Dus . Delen door 1,5 geeft .
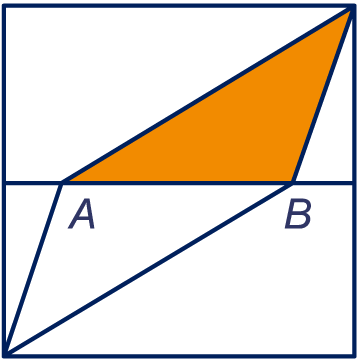
Het middenstuk heeft oppervlakte . De oker driehoek is de helft daarvan en heeft dus oppervlakte 6. De hoogte van die driehoek is 3, dus is zijn basis 4. Dus liggen en 4 cm van elkaar.
De oppervlakte van de vierkanten is 121, 81, 49 en 25 cm2.
Noem de oppervlakte van de witte stukken (de overlappingen) van links naar rechts: , en .
De blauwe oppervlakte is dan en de oker oppervlakte is .
De oppervlaktes verschillen dus 64.
De oppervlakte van het vierkant is cm2.
Oppervlakte kwartcirkel =
Oppervlakte blauw = cm2
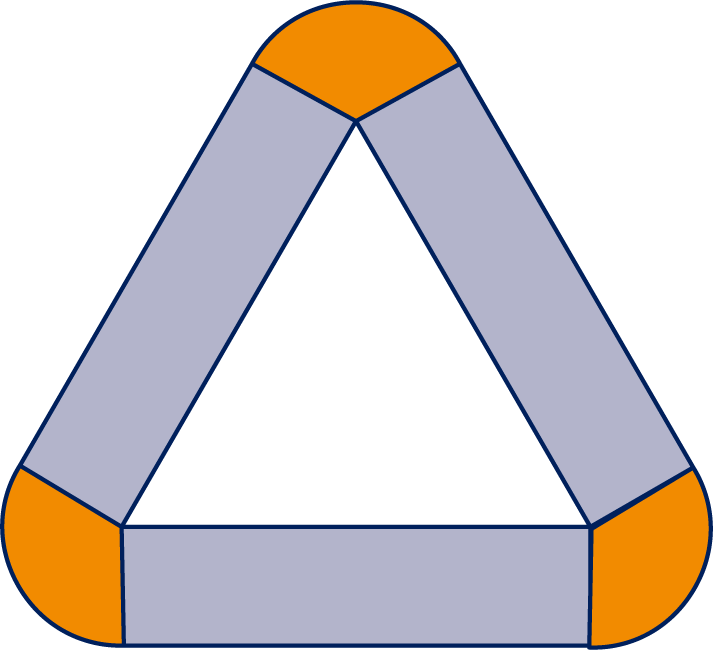
De strook bestaat uit drie rechthoeken (elk met oppervlakte ) en drie sectoren die samen een volle cirkel vormen.
De oppervlakte van de strook is cm2.
