Gevarieerde opgaven

Noem het hoogteverschil $h$ , dan $h = 200 \cdot sin (32 °) \approx 106,0$ meter.

Noem de lengte van de dijkhelling $x$ , dan $sin (32 °) = \frac{18}{x}$ , dus $x = \frac{18}{sin (32 °)} \approx 33,96...$ m, dus 340 dm.

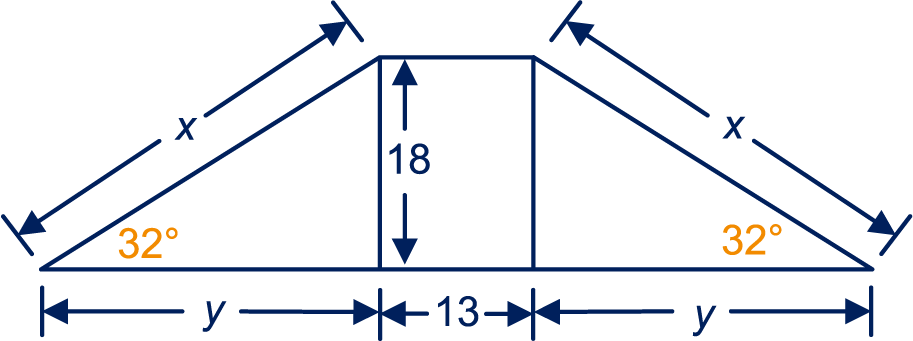
Noem de lengte van een horizontaal stuk onder de dijkhelling $y$ , dan $tan (32 °) = \frac{18}{y}$ , dus $y = \frac{18}{tan (32 °)} \approx 28,8060...$ m.
De gevraagde lengte is $2 y + 13 \approx 71$ meter.

Noem het hoogteverschil $h$ , dan $h = 4 \cdot sin (37 °) \approx 2,4$ meter.
Noem de afstand $a$ , dan $a = 4 \cdot cos (37 °) \approx 3,2$ meter.

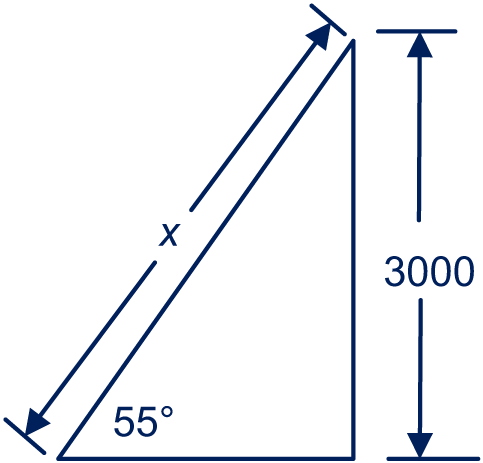
Noem die afstand $x$ , dan $3000 = x \cdot sin (55 °)$ .
Dus $x = \frac{3000}{sin (55 °)} \approx 3662,3$ m, dus $3,7$ km (of $37$ hm).

Zie plaatje.
$y = 240 \cdot cos (35 °) = 196,596...$ cm.
De gevraagde afstand ( $x$ ) is dan $300 - 196,596... \approx 103$ cm.

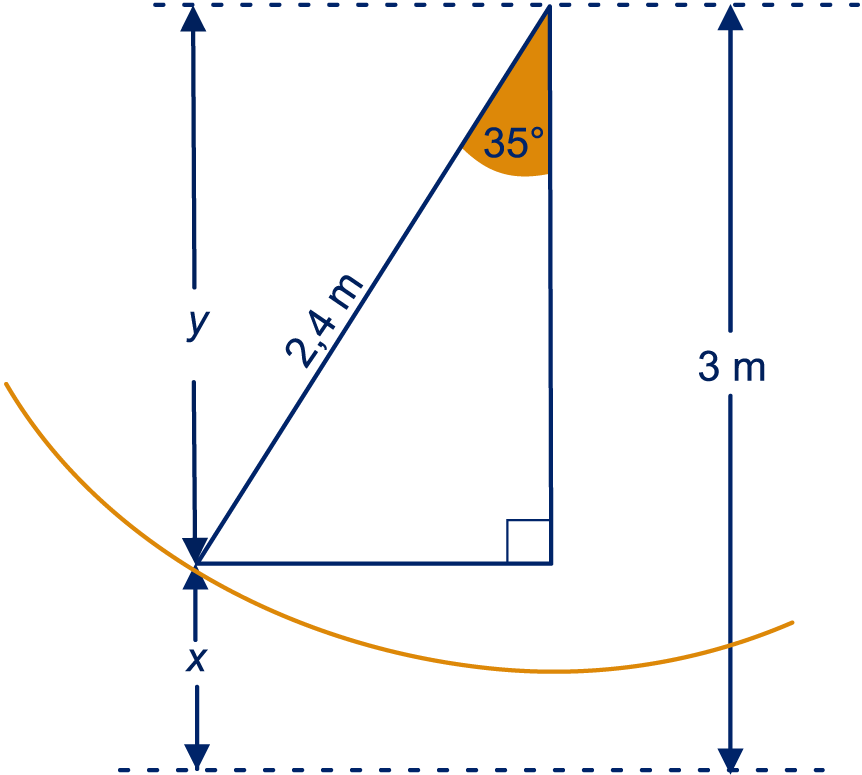
Zie plaatje. De lengte van de buis noemen we $a$ en het hoogteverschil $h$ , dan $9 = a \cdot cos (12 °)$ .
Dus $a = \frac{9}{cos (12 °)} \approx 9,2$ dm, dus $92$ cm.
Nu kun je $h$ met de stelling van Pythagoras berekenen, dit geeft $19$ cm.

Zie plaatje.
$α = \frac{70}{2 π \cdot 70} \cdot 360 ° \approx 57,3 °$
$B M = 70 \cdot cos (57,3 °) \approx 38$ cm.
De gevraagde hoogte is $70 - 38 = 32$ cm.

Zie plaatje.
Noem het hoogteverschil $h$ , dan $h = 50 \cdot sin (3 °) \approx 2,6$ meter.

Driehoeken van roosterpunten

$A B = \sqrt{5}$ , $B C = \sqrt{25} = 5$ en $A C = \sqrt{20}$

${\sqrt{5}}^{2} + {\sqrt{20}}^{2} = 5^{2}$ , want $5 + 20 = 25$

$\cos (β) = \frac{\sqrt{5}}{5}$ , $\tan (β) = \frac{\sqrt{20}}{\sqrt{5}} = 2$

$\sin (γ) = \frac{\sqrt{5}}{5}$ , $\cos (γ) = \frac{\sqrt{20}}{5}$ , $\tan (γ) = \frac{\sqrt{5}}{\sqrt{20}} = \frac{1}{2}$

$β \approx 63 °$ en $γ \approx 27 °$

$\cos (β)$ en $\sin (γ)$ zijn gelijk evenals $\cos (γ)$ en $\sin (β)$ . Verder: $\tan (γ) = \frac{1}{\tan (β)}$ ,
Overstaande rechthoekszijde van $γ$ = aanliggende rechthoekszijde van $β$
Overstaande rechthoekszijde van $β$ = aanliggende rechthoekszijde van $γ$
Schuine zijde is voor beide hetzelfde.

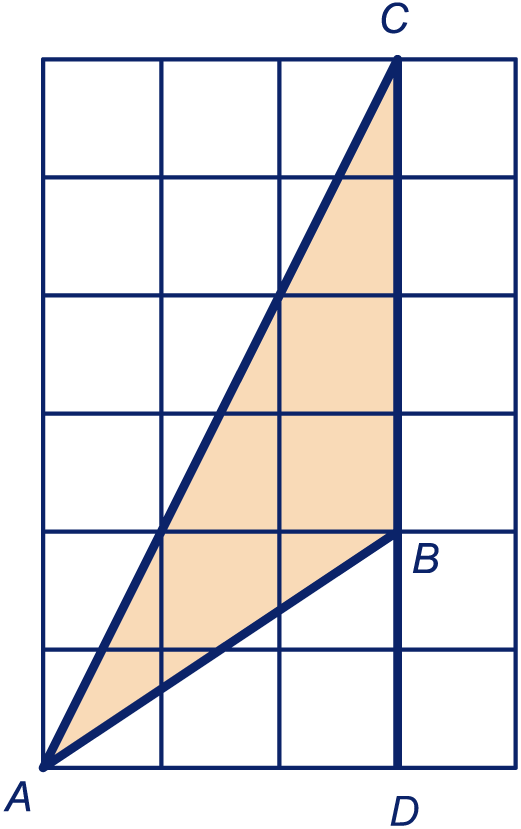
$A B = \sqrt{13}$ , $B C = 4$ en $A C = \sqrt{45}$

$tan (∠ B A D) = \frac{2}{3}$ , dus $∠ B A D \approx 33,7 °$
$tan (∠ C A D) = 2$ , dus $∠ C A D \approx 63,4 °$ dus
$∠ C A B \approx 63,4 ° - 33,7 ° = 29,7 °$

De ruimte in

Hoek $G C A$ .

$A C = \sqrt{4^{2} + 4^{2}} = \sqrt{32}$
$tan (∠ C A G) = \frac{4}{\sqrt{32}}$ , dus $∠ C A G \approx 35 °$

$A M = M B = \sqrt{4^{2} + 4^{2} + 2^{2}} = 6$ .

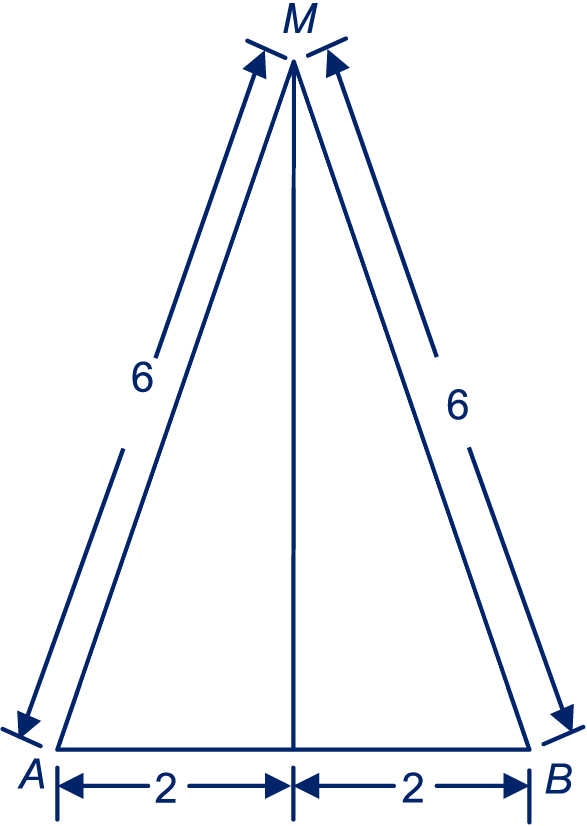
Zie plaatje.
$cos (∠ B A M) = \frac{2}{6}$ , dus $∠ B A M \approx 71 °$

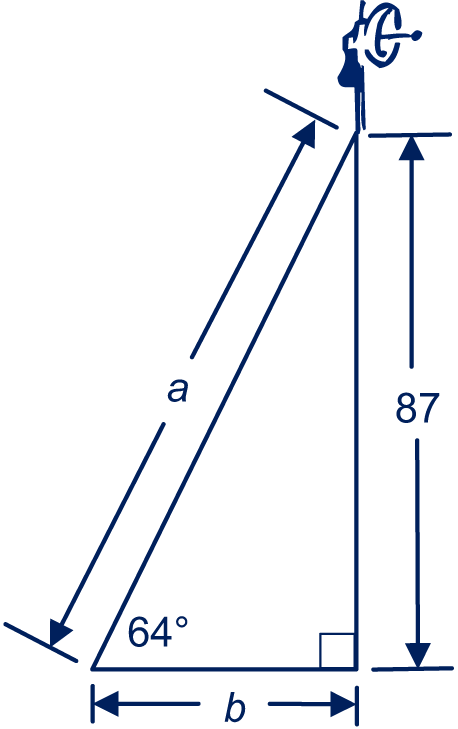
Zie plaatje.
De lengte van de kabel noemen we $a$ en de afstand tot de voet $b$ , dan
$a \cdot sin (64 °) = 87$ , dus $a = \frac{87}{sin (64 °)} \approx 96,8$ meter

Zie plaatje vorige onderdeel.
$b \cdot tan (64 °) = 87$ , dus $b = \frac{87}{tan (64 °)} \approx 42,4$ meter.

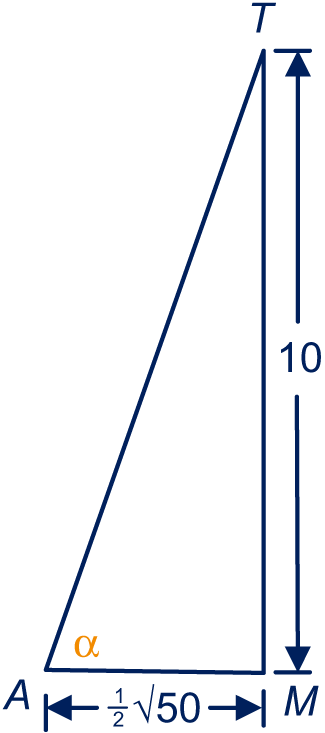
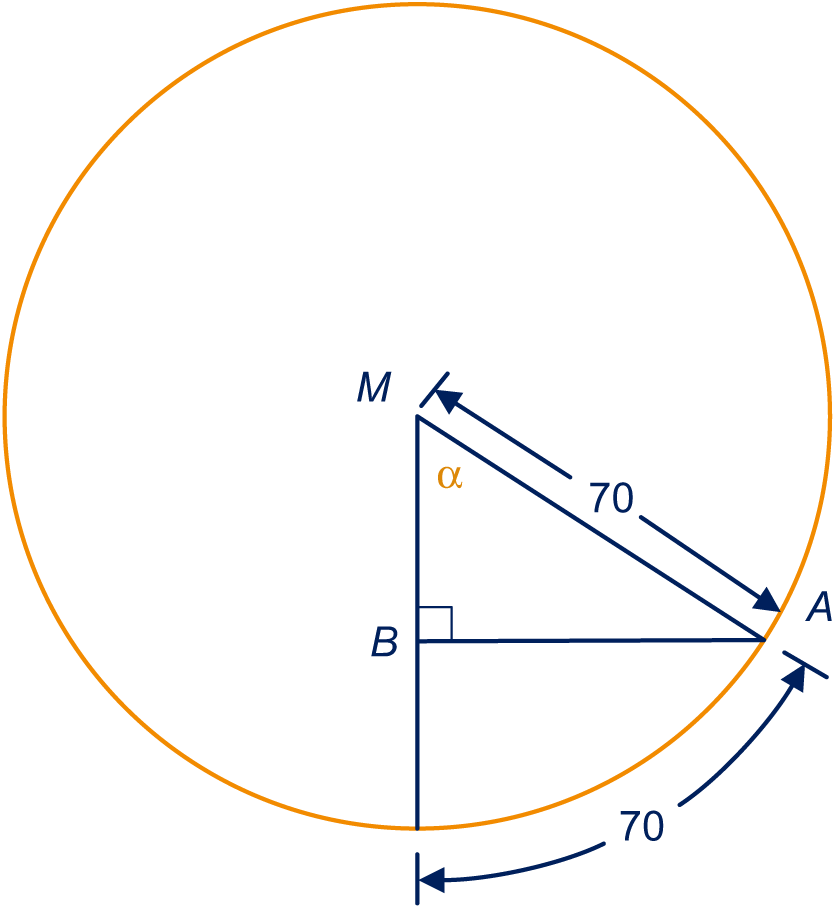
$M$ is het midden van het grondvlak, $T$ de top van de piramide en $A$ een hoekpunt van het grondvlak.
Dan is $A M$ de helft van een diagonaal in het grondvlak. Je moet hoek α berekenen, zie plaatje.
$\tan (α) = \frac{10}{\frac{1}{2} \sqrt{50}}$ , dus $α \approx 71 °$

12s

14s

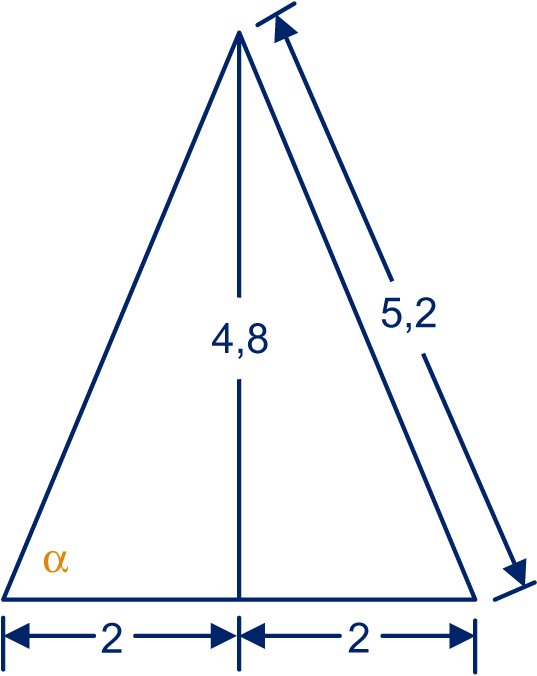
Zie plaatje.
$\tan (α) = 2,4$ , dus $α \approx 67,4 °$ , dus
er zijn twee hoeken van $67,4 °$ en één hoek van $45,2 °$ , dus $67 °$ , $67 °$ en $45 °$ .

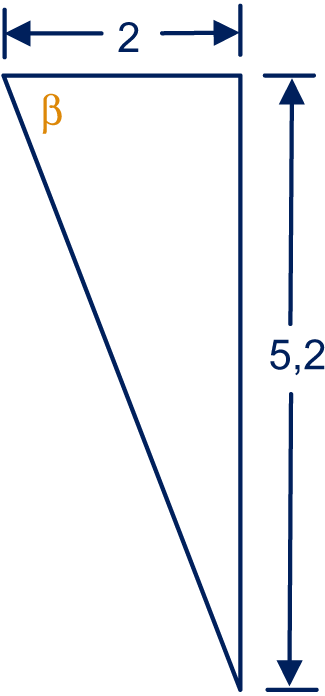
$\tan (β) = 2,6$ , dus $β \approx 69 °$ , die hoeken zijn dus $69 °$ , $21 °$ en $90 °$ .

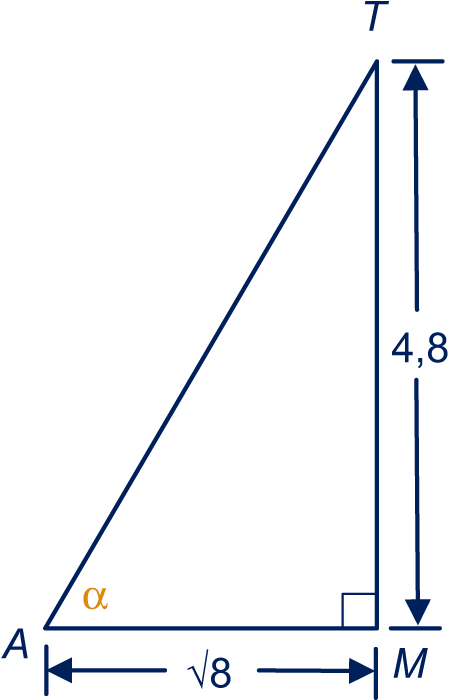
Zie plaatje.
$A$ is een hoekpunt van het vierkante grondvlak. $M$ is het midden van het grondvlak en $T$ is het snijpunt van de twee "nokken".
Dan $\tan (α) = \frac{4,8}{\sqrt{8}}$ dus $α \approx 59 °$ .

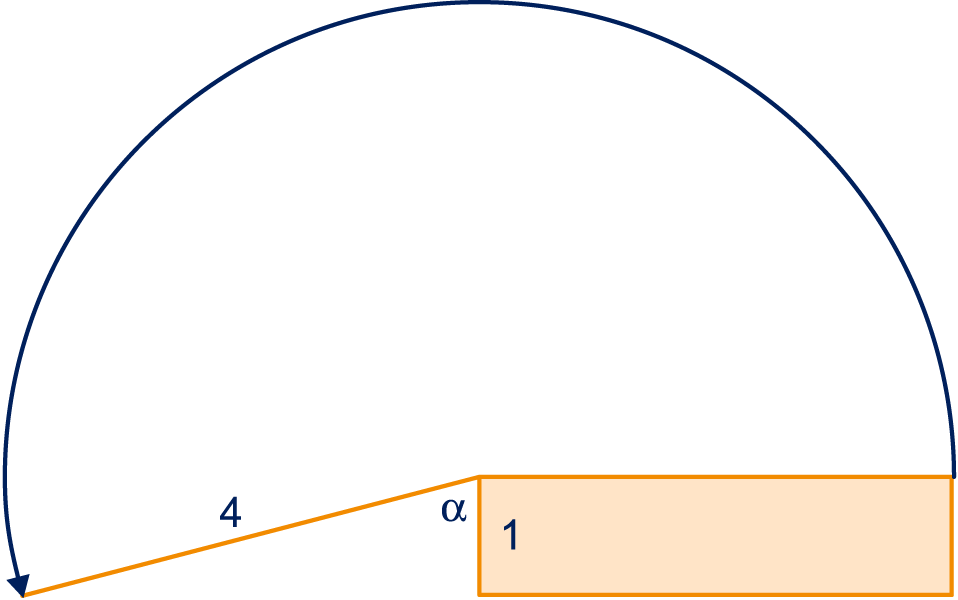
Zie plaatje.
$\cos (α) = \frac{1}{4}$ , dus $α \approx 76 °$ , dus
de gevraagde hoek is $270 ° - 76 ° = 194 °$ .