1.10 Rekenregels >

Hoofdstukken > Combinatoriek en Rekenregels

In deze paragraaf gaan we wat formeler te werk.

Als je met twee dobbelstenen gooit, heb je $36$ mogelijke uitkomsten. Die kun je bijvoorbeeld door paren getallen weergeven, de uitkomstenverzameling:
$(1,1)$ , $(1,2)$ , $(1,3)$ , $(1,4)$ , $(1,5)$ , $(1,6)$ $(2,1)$ , $(2,2)$ , $(2,3)$ , $(2,4)$ , $(2,5)$ , $(2,6)$ $(3,1)$ , $(3,2)$ , $(3,3)$ , $(3,4)$ , $(3,5)$ , $(3,6)$ $(4,1)$ , $(4,2)$ , $(4,3)$ , $(4,4)$ , $(4,5)$ , $(4,6)$ $(5,1)$ , $(5,2)$ , $(5,3)$ , $(5,4)$ , $(5,5)$ , $(5,6)$ , $(6,1)$ , $(6,2)$ , $(6,3)$ , $(6,4)$ , $(6,5)$ , $(6,6)$ .

Een gebeurtenis bestaat uit een deel van de uitkomsten.
Zo bestaat de gebeurtenis het verschil van de aantallen ogen is minstens $2$ uit het deel:
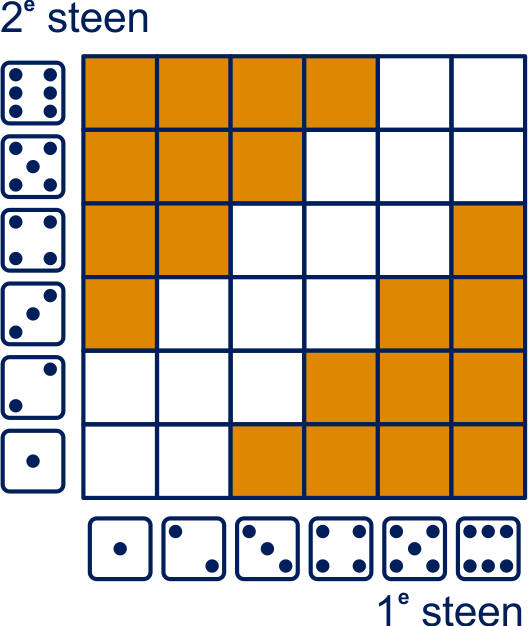
$(1,3)$ , $(1,4)$ , $(1,5)$ , $(1,6)$ , $(2,4)$ , $(2,5)$ , $(2,6)$ , $(3,5)$ , $(3,6)$ , $(4,6)$ , $(3,1)$ , $(4,1)$ , $(5,1)$ , $(6,1)$ , $(4,2)$ , $(5,2)$ , $(6,2)$ , $(5,3)$ , $(6,3)$ , $(6,4)$ .

Je kunt in ons voorbeeld de uitkomsten ook overzichtelijk in een rooster weergeven, zoals we al vaker gedaan hebben. De gebeurtenis het verschil van de aantallen ogen is minstens $2$ is het gekleurde deel van de uitkomstenverzameling.

De verzameling uitkomsten geven we vaak aan met $U$ en een gebeurtenis met een andere hoofdletter, het verschil van de aantallen ogen is minstens 2 zou je bijvoorbeeld met $X$ aan kunnen geven.
We gebruiken de volgende notaties.
# $X$ : het aantal uitkomsten waaruit een gebeurtenis $X$ bestaat;
$P (X)$ : de kans op gebeurtenis $X$ .
De volgende regel geldt: $P (X) = \frac{# X}{# U}$ .
We gaan er hierbij vanuit dat elke uitkomst even waarschijnlijk is.

In het voorbeeld hierboven: $# U = 36$ , $# V = 20$ , dus $P (V) = \frac{# V}{# U} = \frac{20}{36} = \frac{5}{9}$ .

Peter doet herexamen Engels en natuurkunde. Hij slaagt als hij voor Engels minstens 7 haalt of voor natuurkunde minstens 6.
Met het woord of in de zin hierboven bedoelen we natuurlijk: en/of.

Opmerking:

Als $A$ en $B$ twee gebeurtenissen zijn dan bedoelen we met de gebeurtenis $A$ of $B$ : $A$ en/of $B$ .

We gooien twee keer met een dobbelsteen. $A$ de gebeurtenis de som van de ogen is $10$ en $B$ de som van de ogen is $11$ .

Geef $P (A)$ , $P (B)$ en $P (A of B)$ .

Er geldt: $P (A of B) = P (A) + P (B)$ .

$E$ is de gebeurtenis: de eerste keer wordt zes gegooid. $F$ is de gebeurtenis: de tweede keer wordt zes gegooid.

Geef $P (E)$ , $P (F)$ en $P (E of F)$ .

Geldt: $P (E of F) = P (E) + P (F)$ ?

Wat kun je over twee gebeurtenissen $S$ en $T$ opmerken als geldt: $P (S of T) = P (S) + P (T)$ ?

We bekijken de gebeurtenissen $G$ en $H$ , met $G$ : geen van de beide keren wordt zes gegooid en $H$ : minstens één van de beide keren wordt zes gegooid.
In onderdeel c heb je berekend: $P (G) = \frac{11}{36}$ .

Hoe kun je hiermee $P (G)$ berekenen?

Twee gebeurtenissen $X$ en $Y$ sluiten elkaar uit als er geen uitkomsten zijn die zowel tot $X$ als tot $Y$ behoren.
Er geldt: $P (X of Y) = P (X) + P (Y)$ .

Twee gebeurtenissen $X$ en $Y$ heten complementair als elke uitkomst óf tot $X$ óf tot $Y$ behoort.
Er geldt: $P (X) + P (Y) = 1$ .

Voorbeeld:

In opgave 79 sluiten de gebeurtenissen $A$ en $B$ elkaar uit; de gebeurtenissen $G$ en $H$ zijn complementair.

Van een groep mensen leest $30$ % de Volkskrant, $20$ % de NRC en $57$ % geen van beide. Uit de de groep wordt één persoon gekozen.
$V$ is de gebeurtenis: die persoon leest de Volkskrant en $N$ is de gebeurtenis: die persoon leest de NRC.

Sluiten $V$ en $N$ elkaar uit? Hoe zie je dat aan de percentages?

Hoeveel procent van deze mensen leest beide kranten?

Geef $P (V)$ , $P (N)$ , $P (V of N)$ , $P (V en N)$

Wat is het verband tussen de vier getallen die je in het vorige onderdeel berekend hebt?

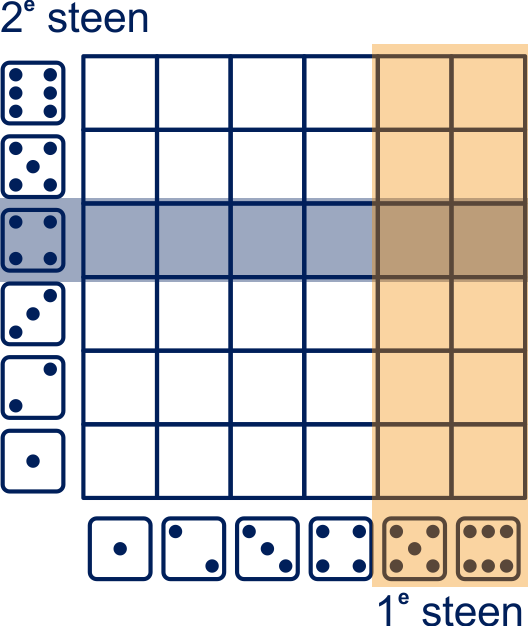
We gooien twee keer met een dobbelsteen.
Hiernaast zijn gekleurd de verzamelingen $S$ : de eerste keer gooi je minstens vijf en $T$ : de tweede keer gooi je vier.
Met $S \cup T$ (spreek uit de vereniging van $S$ en $T$ ) geven de verzameling aan bestaande uit de uitkomsten: de eerste keer gooi je minstens vijf of de tweede keer gooi je vier. Dat is de verzameling van alle gekleurde worpen in de figuur.
Met $S \cap T$ (spreek uit de doorsnede van $S$ en $T$ ) geven we de verzameling aan bestaande uit de uitkomsten: de eerste keer gooi je minstens vijf en de tweede keer gooi je vier. Dat is de verzameling van alle dubbel gekleurde worpen in de figuur.

John Venn

John Venn (1834-1923) was begin twintigste eeuw de bekendste logicus ter wereld. Hij schreef verschillende boeken over logica, waaronder The Logic of Chance en Symbolic Logic. Venn werd onder meer bekend door de introductie van het naar hem vernoemde Venndiagram, een grafische voorstelling van logische relaties tussen meerdere verzamelingen.
Uit Wikipedia

In een Venn-diagram kun je de vereniging en de doorsnede van twee verzamelingen $A$ en $B$ weergeven, zie de figuur hieronder.

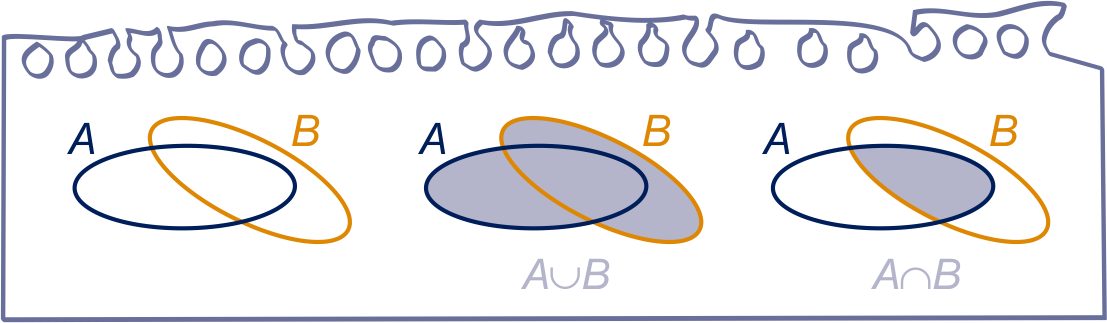
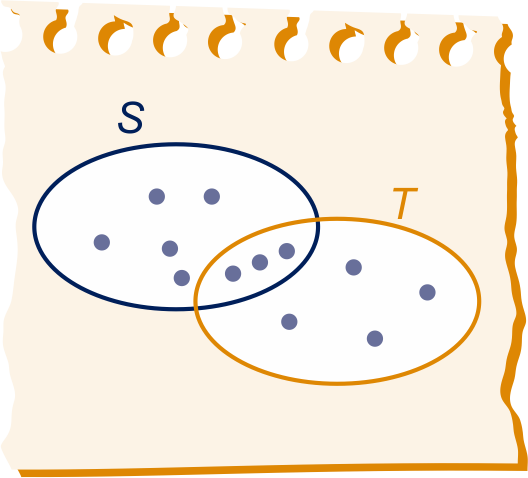
In het Venndiagram hiernaast stelt elke stip een element voor van de verzameling waarin hij getekend is. Zo heeft $S$ $8$ elementen.

Wat is het verband tussen # $S$ , # $T$ , # $S \cup T$ en # $S \cap T$ ?

Somregel
Gegeven zijn twee gebeurtenissen $A$ en $B$ , dan:
$P (A of B) = P (A) + P (B) - P (A en B)$ .

Bovenstaande regel volgt uit de volgende regel voor twee verzamelingen $S$ en $T$ :
$# S + # T = # S \cup T + # S \cap T$ . In het volgende kijken we naar onafhankelijkheid van twee gebeurtenissen. Daartoe een inleiding uit Wikipedia (12-09-2007).

Als we willekeurig een mens op aarde aanwijzen, zal de kans dat het een vrouw blijkt te zijn gelijk zijn aan $\frac{1}{2}$ . Vertelt iemand ons dat de aangewezen persoon uit Afrika komt, dan nog zal het in de helft van de gevallen een vrouw blijken te zijn, dat wil zeggen ook dan zal de kans op een vrouw $\frac{1}{2}$ zijn.
Anders wordt het voor de kans op een donkere huidskleur. Mogelijk is die kans ca $0,1$ - $0,2$ . Weten we echter dat de gekozen persoon uit Afrika komt, dan zal de kans op een donkere huidskleur praktisch $1$ bedragen. Het optreden van de gebeurtenis A(frika) verandert niets aan de kans op de gebeurtenis V(rouw), maar wel aan de kans op de gebeurtenis D(onkere huidskleur). We noemen daarom de gebeurtenissen A en V (onderling) onafhankelijk. De gebeurtenissen A en D daarentegen heten (onderling) afhankelijk. Een formele definitie wordt meestal in termen van het gelijktijdig optreden van beide gebeurtenissen gegeven, waaruit de bovengenoemde eigenschap volgt.

Een voorbeeld met dobbelstenen
Ad gooit twee keer met een dobbelsteen. Hij verklapt je dat de som van het aantal gegooide ogen even is.

Wat is dan de kans dat de som van het aantal ogen minstens $8$ is?

$A$ is de gebeurtenis: de som van het aantal ogen is even.
$B$ is de gebeurtenis: de som van het aantal ogen is minstens $8$ .
De kans die je in a hebt berekend noemen we een voorwaardelijke kans: de kans dat de som van het aantal ogen minstens $8$ is onder de voorwaarde dat de som van het aantal ogen even is.

$C$ is de gebeurtenis: de eerste keer wordt meer dan $4$ gegooid.

Bereken de kans op $A$ onder de voorwaarde $C$ .

Bereken de kans op $B$ onder de voorwaarde $C$ .

Notatie
Met $B | A$ bedoelen we $B$ onder voorwaarde $A$ .

In opgave 82 a staat een voorbeeld van $B | A$ .
Als je het goed hebt gedaan heb je het antwoord gevonden met de volgende regel: $P (B | A)$ $= \frac{# A \cap B}{# A}$ .
Dus $P (B | A) = \frac{# A \cap B}{# A}$ $= \frac{\frac{# A \cap B}{# U}}{\frac{# A}{# U}} = \frac{P (A \cap B)}{P (A)}$

$A$ en $B$ zijn gebeurtenissen, dan $P (B | A)$ $= \frac{P (A \cap B)}{P (A)}$ .

Op weg naar school passeert Anne twee verkeerslichten. Die werken onafhankelijk van elkaar. Voor het eerste licht moet ze met $30$ % kans wachten, voor het tweede met $20$ % kans. Op school vertelt ze dat voor één van de lichten heeft moeten wachten.

Bereken de kans dat dat voor het eerste licht was in twee decimalen.

Is lucifer trekken eerlijk?
Bij lucifertrekken tussen bijvoorbeeld vier spelers, houdt één van hen vier lucifers in de hand waarvan er één korter is dan de andere drie. Maar dat kun je niet zien als je naar de vier stukjes kijkt die zichtbaar zijn. Om beurten trekken de drie anderen een lucifer tot de kortere lucifer getrokken is. Die speler is dan de klos. Als de kortere lucifer niet getrokken wordt, verliest de speler die de lucifers vasthield.

Wat is de kans dat de eerste speler de kortere lucifer trekt?

Wat is de kans dat de derde speler de kortere lucifer trekt?

Is het spel eerlijk?

In een vaas zitten twee rode en drie witte ballen. Arno trekt twee keer een bal uit de vaas zonder terugleggen.
$S$ is de gebeurtenis: de eerste bal is rood,
$T$ is de gebeurtenis: de tweede bal is rood.

Laat zien dat $P (T) = \frac{2}{5}$ .

Geef $P (S \cap T)$ .

Bereken $P (T | S)$ .

Arno herhaalt het experiment, met dit verschil dat hij nu met terugleggen trekt.
$S$ is de gebeurtenis: de eerste bal is rood,
$T$ is de gebeurtenis: de tweede bal is rood.

Bereken $P (S)$ , $P (T)$ en $P (S \cap T)$ .

Bereken $P (T | S)$ .

Definitie
Twee gebeurtenissen $S$ en $T$ zijn onafhankelijk als
$P (T | S)$ $= P (T)$ .
Dit komt op hetzelfde neer als:
de gebeurtenissen $S$ en $T$ zijn onafhankelijk als
$P (S \cap T)$ $= P (S) \cdot P (T)$ .

In opgave 85 vind je $P (T | S)$ $\neq P (T)$ , in opgave 86 $P (T | S)$ $= P (T)$ .
Vergelijk dit met het verhaal uit Wikipedia.
In opgave 85 verandert de kans op $T$ als je die onder de voorwaarde $S$ bekijkt omdat $S$ en $T$ in die opgave afhankelijk zijn.
In opgave 86 verandert die kans niet, omdat $S$ en $T$ daar onafhankelijk zijn.

Laat zien dat $P (T | S)$ $= P (T)$ op hetzelfde neerkomt als $P (S \cap T) = P (S) \cdot P (T)$

Twee ronde kartonnetjes worden (concentrisch) op elkaar geplakt. De schijf die je zo krijgt wordt gedraaid en op een willekeurig moment gestopt. Er wordt genoteerd wat de pijl aanwijst. Dat kan zijn $R$ (rood), $B$ (blauw), $G$ (geel) of $P$ (paars). In het plaatje wordt $G$ en $R$ aangewezen. De kans daarop is $\frac{1}{8}$ .

Bereken $P (B | G)$ , $P (R | G)$ en $P (P | G)$

Zijn $B$ en $G$ onafhankelijk?

Kun je de twee kartonnetjes zó op elkaar plakken dat $B$ en $G$ onafhankelijk zijn?

Ad gooit twee keer met een dobbelsteen. $A$ is de gebeurtenis: met de eerste steen wordt hoger dan vier gegooid.
$B$ is de gebeurtenis: de som van de ogen is lager dan zes.
$C$ is de gebeurtenis: de som van de ogen is even.

Zijn $A$ en $B$ onafhankelijk?
En $B$ en $C$ ?
En $A$ en $C$ ?