Gegeven is een experiment met uitkomstenverzameling $U$. De kans op een gebeurtenis $G$ is: $\frac{\text{het aantal elementen van }G}{\text{het aantal elementen van }U}$.

Met een kansboom kun je op een elementaire manier kansen berekenen.
De kans aan een uiteinde kun je berekenen door de kansen die langs de takken staan met elkaar te vermenigvuldigen.

Voorbeeld 1

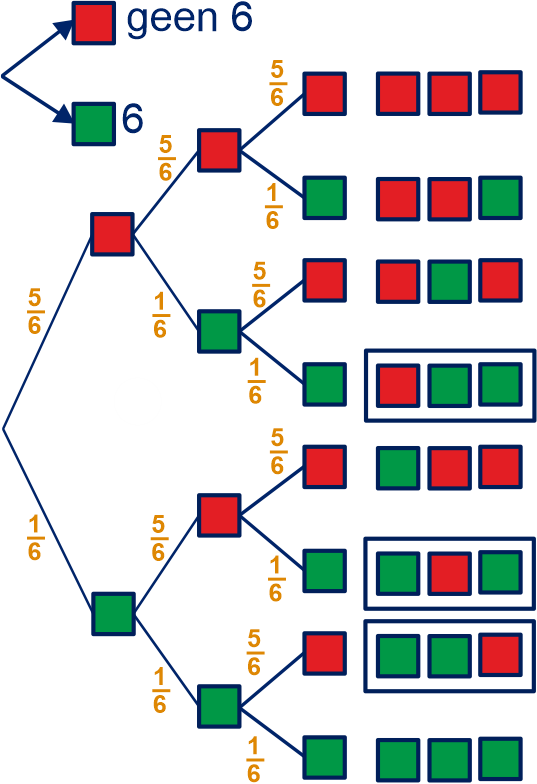
Je gooit drie keer met een dobbelsteen. Wat is de kans dat je twee keer $6$ ogen gooit?
De kansboom waarmee je de gevraagde kans kunt berekenen staat hiernaast.
De gevraagde kans vind je door de kansen op de uitslagen in de hokjes op te tellen, dus: $\frac{5}{6}\cdot \frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{5}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}\cdot \frac{5}{6}=\frac{15}{216}$.





Voorbeeld 2

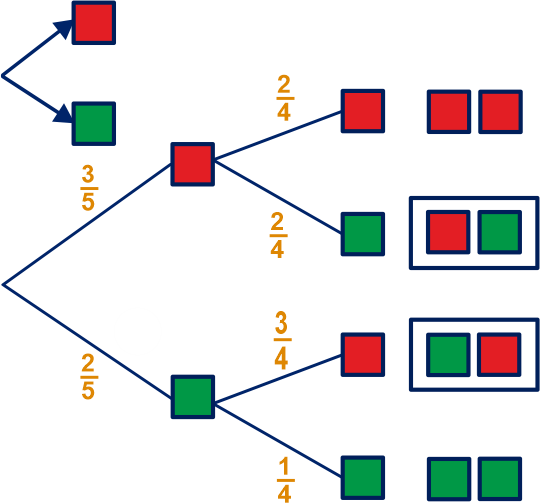
Uit een vaas met twee groene en drie rode ballen, trek je achter elkaar, zonder terugleggen, twee ballen.
Wat is de kans op een rode en een groene bal? De kansboom waarmee je de gevraagde kans kunt berekenen staat hiernaast.
De gevraagde kans vind je door de kansen op de uitslagen in de hokjes op te tellen, dus: $\frac{3}{5}\cdot \frac{2}{4}+\frac{2}{5}\cdot \frac{3}{4}=\frac{6}{20}$.

In voorbeeld 1 spreek je over een probleem met terugleggen en in voorbeeld 2 zonder terugleggen en wel hierom.
Je doet iets een aantal keren (in voorbeeld 1 gooien met een dobbelsteen, in voorbeeld 2 trekken van een bal uit een vaas).
In voorbeeld 1 veranderen de kansen op zes/geen zes in een volgende keer niet, in voorbeeld 2 hangt de kans op rood/groen in een volgende keer af van wat er de vorige keer getrokken is.

Een rijtje dingen (bijvoorbeeld getallen) waarbij de volgorde van belang is, noemen we ook wel een rangschikking of permutatie.

Er zijn $n\cdot (n-1)\cdot (n-2)\cdot \dots \cdot 3\cdot 2\cdot 1$ verschillende rangschikkingen van $n$ verschillende dingen.
We noteren $n\cdot (n-1)\cdot (n-2)\cdot \dots \cdot 3\cdot 2\cdot 1$ met $n$! (spreek uit: $n$ faculteit).

Bijvoorbeeld: de acht getallen $5$, $7$, $9$, $11$, $13$, $15$, $17$, $19$ kun je op $8!=8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1=40.320$ manieren op een rij zetten.

Je kunt ook kortere rijtjes van bijvoorbeeld zes getallen van die acht getallen maken. Je spreekt dan van rangschikkingen (of permutaties) van zes uit acht.
Het aantal permutaties van $k$ uit $n$ is $\frac{n!}{(n-k)!}$.
Op veel rekenmachines en de GR vind je dit aantal met de optie $n$P$k$.
Je kunt ook zes getallen uit die acht nemen zonder op de volgorde te letten, dan spreek je van een combinatie of greep van zes uit acht.

Het aantal combinaties van $k$ uit $n$ noteren we met $\left(\begin{array}{c}n\\ k\end{array}\right)$.
De getallen $\left(\begin{array}{l}n\\ k\end{array}\right)$ noemen we combinatiegetallen. Er geldt: $\left(\begin{array}{c}n\\ k\end{array}\right)=\frac{n!}{(n-k)!\cdot k!}$.
Op veel rekenmachines en de GR vind je dit aantal met de optie $n$C$k$.

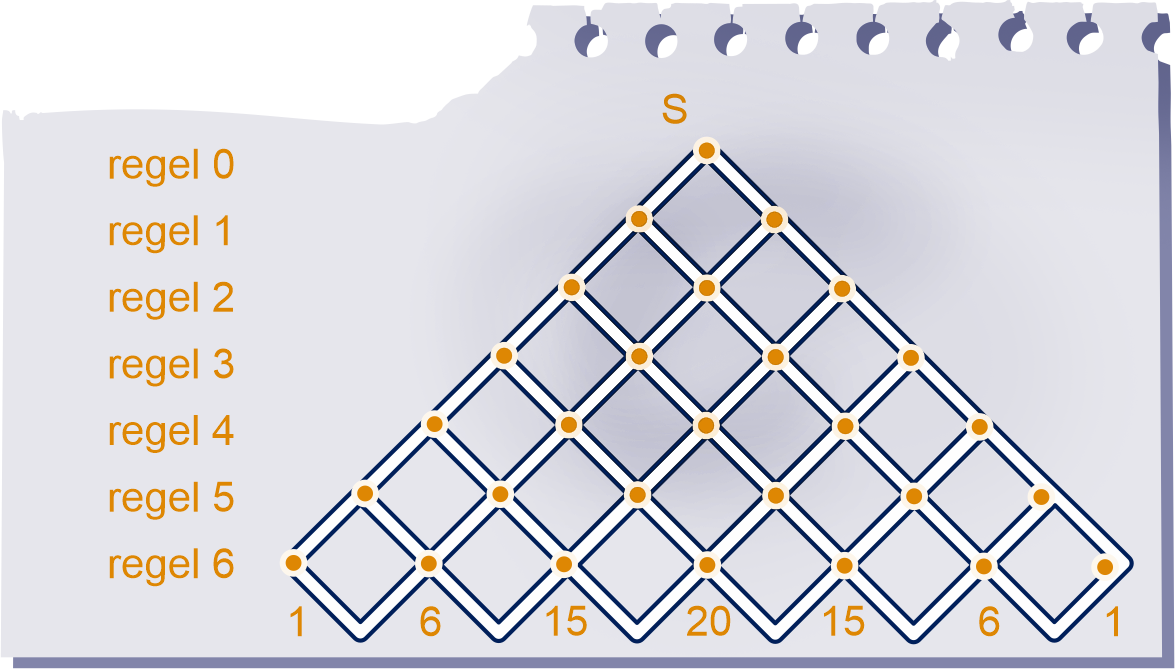
Bekijk het rechthoekig stratenplan hieronder. Zet je bij elke hoek het aantal kortste wegen van $S$ naar die hoek, dan krijg je de driehoek van Pascal. In de figuur is dat bij de zesde regel gedaan.
Je krijgt dan de combinatiegetallen $\left(\begin{array}{c}6\\ 0\end{array}\right)$, $\left(\begin{array}{c}6\\ 1\end{array}\right)$, $\left(\begin{array}{c}6\\ 2\end{array}\right)$, $\left(\begin{array}{c}6\\ 3\end{array}\right)$, $\left(\begin{array}{c}6\\ 4\end{array}\right)$, $\left(\begin{array}{c}6\\ 5\end{array}\right)$, $\left(\begin{array}{c}6\\ 6\end{array}\right)$.
In de driehoek van Pascal staat het $\left(\begin{array}{l}n\\ k\end{array}\right)$ in de $n$-de regel op plaats $k$.

Veel kansexperimenten kun je terugbrengen tot het trekken uit een vaas met ballen.
Als je niet teruglegt, kun je dat soort kansen berekenen met combinatiegetallen.

Voorbeeld 3
Je trekt uit een vaas met tien witte en vijf zwarte ballen zonder terugleggen drie ballen.
De kans dat je twee zwarte trekt kun je als volgt berekenen.
Drie ballen uit de vaas trekken kan op $\left(\begin{array}{c}15\\ 5\end{array}\right)$ manieren. Twee zwarte ballen trekken op $\left(\begin{array}{c}5\\ 2\end{array}\right)$ manieren en één witte op $\left(\begin{array}{c}10\\ 1\end{array}\right)$ manieren.
De gevraagde kans is dus: $\frac{\left(\begin{array}{c}5\\ 2\end{array}\right)\cdot \left(\begin{array}{c}10\\ 1\end{array}\right)}{\left(\begin{array}{c}15\\ 5\end{array}\right)}=\frac{100}{3003}\approx \mathrm{0,033}$.