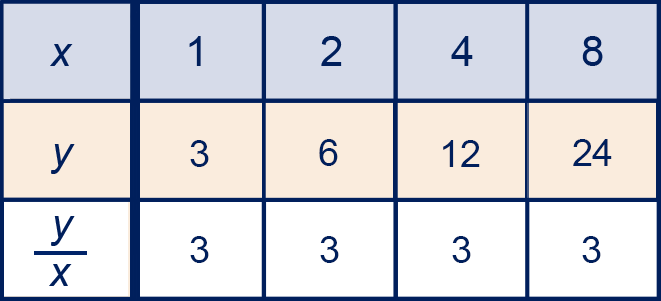
Een
evenredig verband
tussen en heeft een formule in de gedaante .
De verhouding tussen en is altijd hetzelfde.
De grafiek is een rechte lijn door .
Het getal is de
evenredigheidsconstante.
Kenmerk: als de met een factor
wordt vermenigvuldigd, dan wordt
ook met factor
vermenigvuldigd.
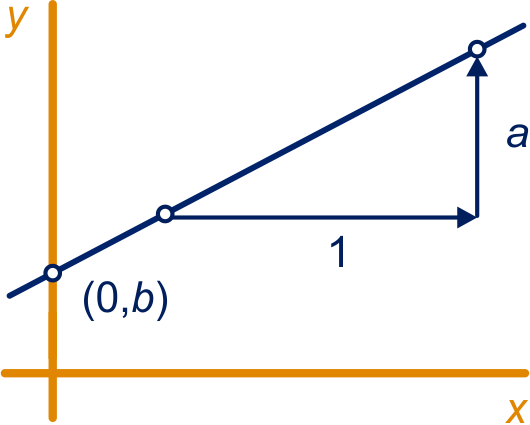
De verhouding tussen de toenames van en , is altijd hetzelfde, d.w.z. en dit is de richtingscoëfficiënt van de lijn (of helling, hellingsgetal, hellingscoëfficiënt).
De grafiek is een rechte lijn door het punt .
Ook de grafiek bij de formule is een rechte lijn.
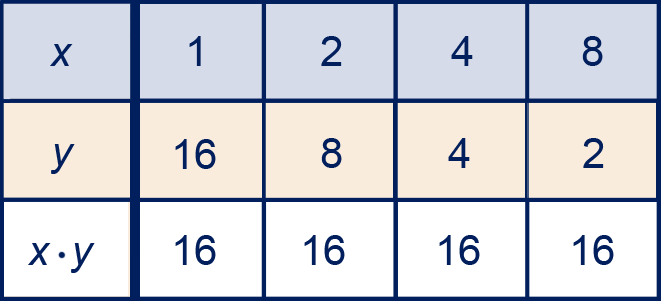
Een
omgekeerd evenredig verband
tussen en heeft een formule in de gedaante .
Het product is altijd hetzelfde.
Het getal is de
evenredigheidsconstante.
De grafiek is (een deel van) een hyperbool.
Kenmerk: als de met een factor
wordt vermenigvuldigd, dan wordt
met factor
vermenigvuldigd.
Als je bij een lineair verband twee paren gegeven hebt, kun je bij elke waarde van de bijbehorende waarde van uitrekenen, en omgekeerd.
Als de waarde van tussen de twee gegevens in ligt, spreken we van
interpolatie, anders van
extrapolatie.
Schematisch:
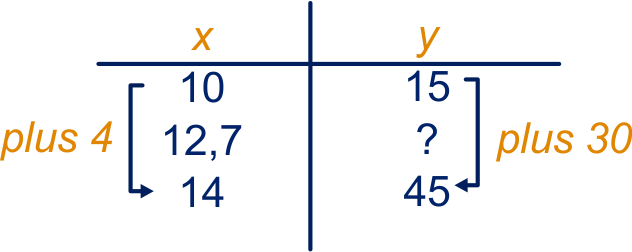
neemt met toe als met toeneemt
neemt met toe als met toeneemt
neemt met toe als met toeneemt
bij hoort
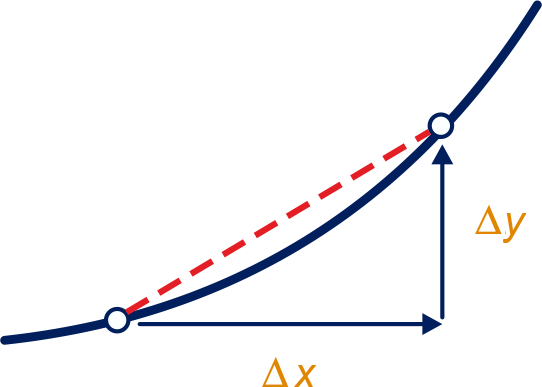
Gegeven is een verband tussen en
.
De gemiddelde toename (of gemiddelde helling) van op het
-interval kun je als volgt met het
rekenschema uitrekenen.
De gemiddelde toename is dan: .
Het is tevens de richtingscoëfficiënt van het verbindingslijstuk tussen de twee punten.
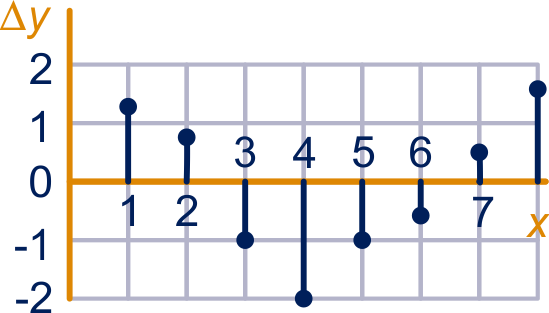
Als we voortdurend met bijvoorbeeld laten toenemen, krijgen we een rij toenames van .
Het
toenamediagram
is een grafische weergave van deze toenames. Bij wordt de toename van uitgezet als toeneemt van naar .
De vorm bij een -interval heet het differentiequotiënt en geeft de helling van de rechte lijn tussen twee punten op de grafiek.
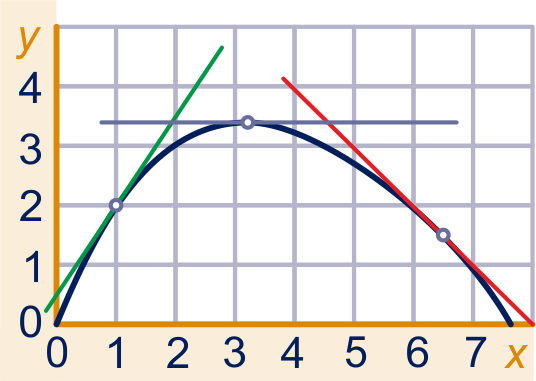
Maak je het -interval rondom een bepaalde waarde van
erg klein, bijvoorbeeld
,
dan krijg je met het differentiequotient de
helling in het punt.
Dat is de richtingscoëfficiënt van de
raaklijn aan de grafiek in dat punt.
Je kunt de helling in een punt ook vinden door de raaklijn te tekenen en van de raaklijn de richtingscoëfficiënt te bepalen.
De helling in een top (of dal) van de grafiek is nul.
De gelijkheid beschrijft een rechte lijn.
De ongelijkheid
beschrijft het gebied onder die rechte lijn.
De ongelijkheid
beschrijft het gebied boven die rechte lijn.
Als de ongelijkheid een andere vorm heeft, kun je een punt invullen om te bepalen welk gebied bij de ongelijkheid hoort.
Als er meer ongelijkheden een rol spelen, dan kun je bij elke ongelijkheid een grafiek tekenen en het bijbehorende gebied onder of boven de lijn aangeven. Het gebied dat voldoet aan alle ongelijkheden noemen we het toegestane gebied.