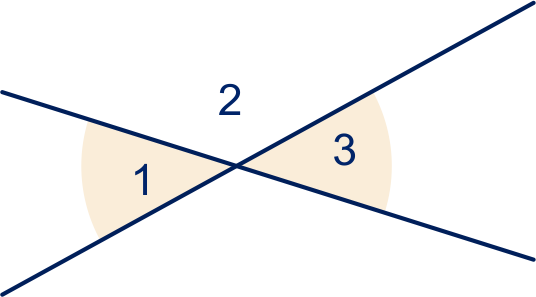
De hoeken en zijn samen evenals de hoeken en . Dus zijn de hoeken en even groot.
;
;
Dus:
.
Omdat en volgt dat
.
, want is het midden van lijnstuk .
, want
is het spiegelbeeld van . Dus .
Op dezelfde manier vind je .
,
want is het spiegelbeeld van ,
, want ,
, want .
Dus .
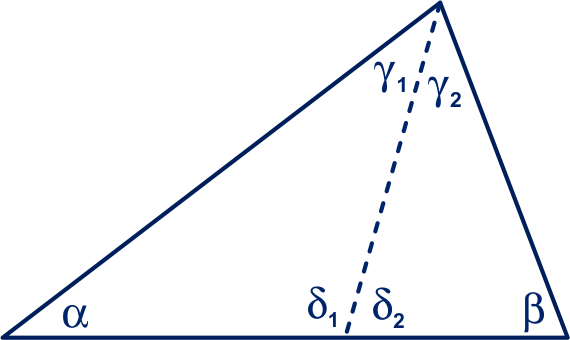
Noem de hoekpunten ,
en .
Omdat , is
.
Net zo is .
Dus .
Omdat de hoekensom in een driehoek is, geldt:
.
De buitenhoek bij (gestrekte hoek) en (hoekensom driehoek). Dus: de buitenhoek bij .
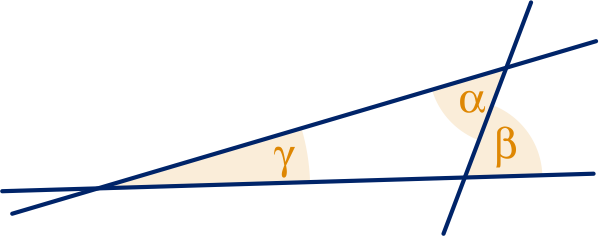
Als de lijnen niet evenwijdig zouden zijn, dan zouden ze elkaar snijden. Dan zou , dus .
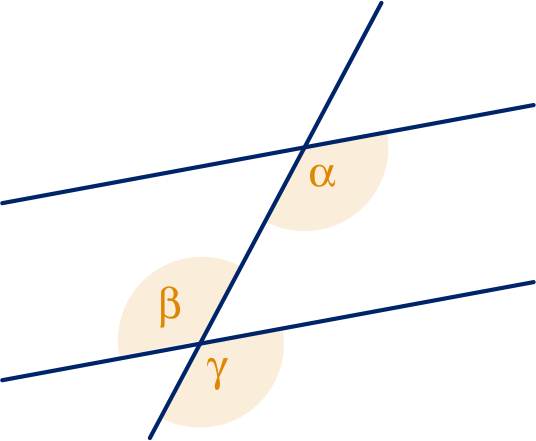
Uit opgave 1 volgt: ;
Uit het gegeven volgt dan: .
Uit opgave 6 volgt dan dat de twee lijnen evenwijdig zijn.
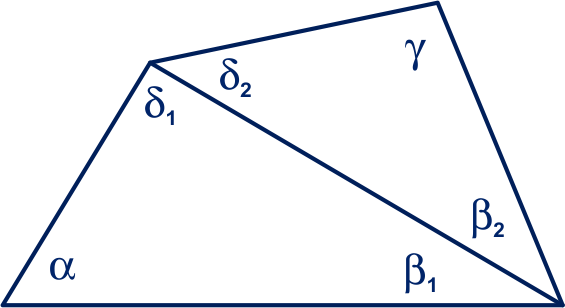
Verdeel de vierhoek in twee driehoeken.
Er geldt: en
, dus:
.
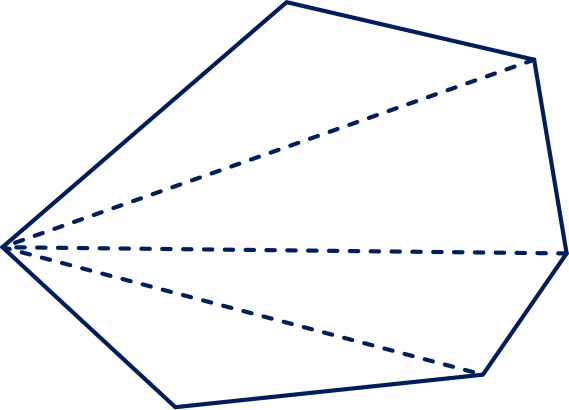
Je kunt de veelhoek vanuit een hoekpunt verdelen is driehoeken. (In de figuur is dat gedaan voor een zeshoek). Dus de hoekensom is graden.
De twee stompe hoeken noemen we en de twee scherpe .
Zie figuur 1, en
Er geldt: (overstaande hoeken).
Dus (dat laatste vanwege gestrekte hoek).
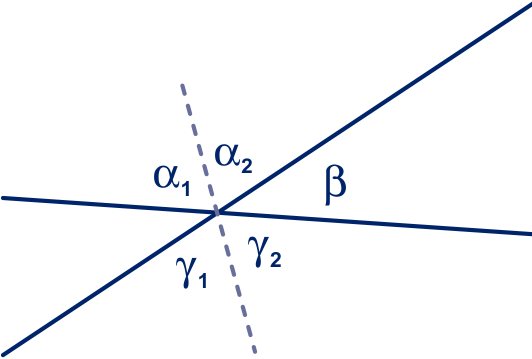
figuur 1
|
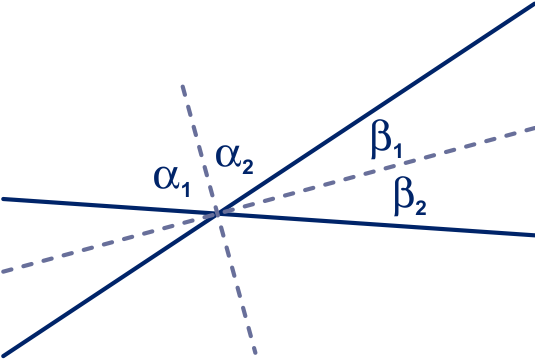
figuur 2
|
Zie figuur 2. en
.
Dus: .
Driehoek is gelijkbenig, dus de hoeken
en zijn even groot.
Dus .
Stel dat de lijn geen raaklijn is. Dan heeft de lijn nog
een tweede punt met de cirkel gemeen, zeg punt .
Maar dan staat niet loodrecht op de lijn, volgens opgave 11.
Dit is in tegenspraak met het gegeven.
Dus is de lijn wel een raaklijn.
Stel dat
niet loodrecht staat op de lijn. De loodrechte
projectie van op de lijn is dan een ander punt
dan ; noem dat .
Spiegel punt in de lijn
.
Het beeldpunt ligt op de
raaklijn en .
Dus ligt ook op de cirkel. Dus
raaklijn gaat door twee punten van de cirkel en dat kan
niet. Dus staat wel loodrecht op de lijn.
De drie driehoeken hebben alle een rechte hoek.
De drie driehoeken hebben alle een hoek α.
Van de driehoeken en
is dat duidelijk.
In driehoek geldt:
.
De overgebleven hoeken van de drie driehoeken zijn
dan automatisch ook gelijk. De driehoeken hebben
gelijke hoeken en zijn dus gelijkvormig.
en
.
(allebei ) (en dus
automatisch ook ).
De driehoeken hebben gelijke hoeken en zijn dus gelijkvormig.
De twee driehoeken hebben beide een rechte hoek en de hoeken en zijn even groot.
Nee, bijvoorbeeld het vierkant met zijden is niet gelijkvormig met de rechthoek met zijden en . Beide hebben wel vier rechte hoeken.
