1

Twee cirkels met dezelfde straal, twee lijnstukken van dezelfde lengte, twee rechte hoeken.

2

a

ja, ja,ja,ja, nee, nee

b

Als twee hoeken hetzelfde zijn, dan ook de derde, want de hoekensom in een driehoek is $180 °$ .

c

Als twee hoeken hetzelfde zijn, dan ook de derde.

d

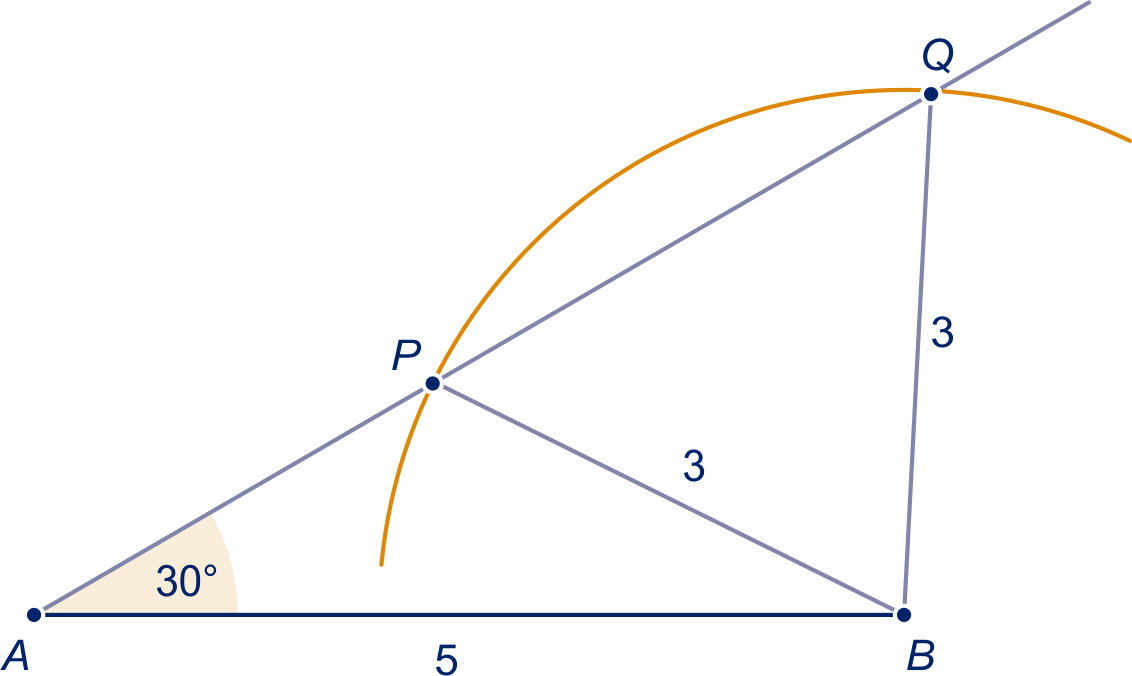
Driehoek $A B P$ en driehoek $A B Q$ voldoen beide.

e

In het vorige onderdeel liggen de punten $P$ en $Q$ komen dan symmetrisch ten opzichte van hun midden $A$ .
In het geval ZZR vallen $P$ , $Q$ en $A$ samen.
Congrueentie volgt in dit geval ook uit de stelling van Pythagoras, want de derde zijde moeten de driehoeken volgens deze stelling ook gelijk hebben.

3

Het snijpunt van de middelloodlijn met lijnstuk $A B$ noemen we $D$ . Neem aan dat $P$ een punt op de middelloodlijn is. Dan zijn de driehoeken $A D P$ en $B D P$ congruent (ZZR), dus $| A P | = | B P |$ .

4

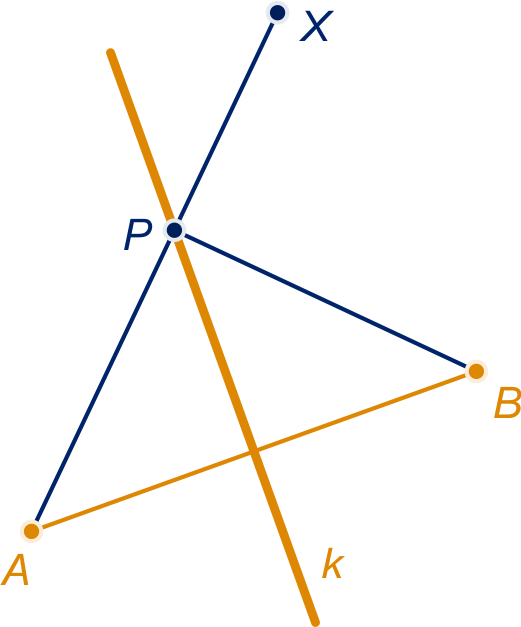
Het snijpunt van lijn $A X$ met $k$ noemen we $P$ . Dan: $| A P | = | B P |$ en $| B X | < | P X | + | B P |$ (driehoeksongelijkheid),
dus $| B P | < | P X | + | A P |$ .

5

$| B S | = | C S |$ , want $S$ ligt op de middelloodlijn van $B C$ .
Hieruit volgt dat $| A S | = | C S |$ . Dus $S$ ligt op de middelloodlijn van $A C$ .

6

Het punt $S$ van de vorige opgaven ligt even ver van de hoekpunten $A$ , $B$ en $C$ .
Noem die gelijke afstand $r$ . De punten $A$ , $B$ en $C$ liggen op de cirkel met middelpunt $S$ en straal $r$ : dat is de omgeschreven cirkel.

7

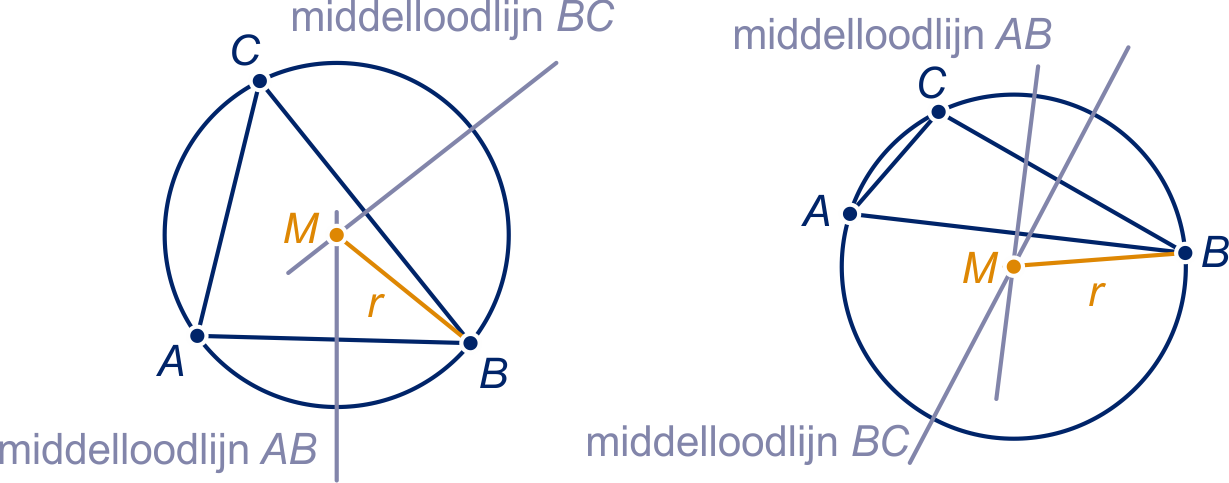
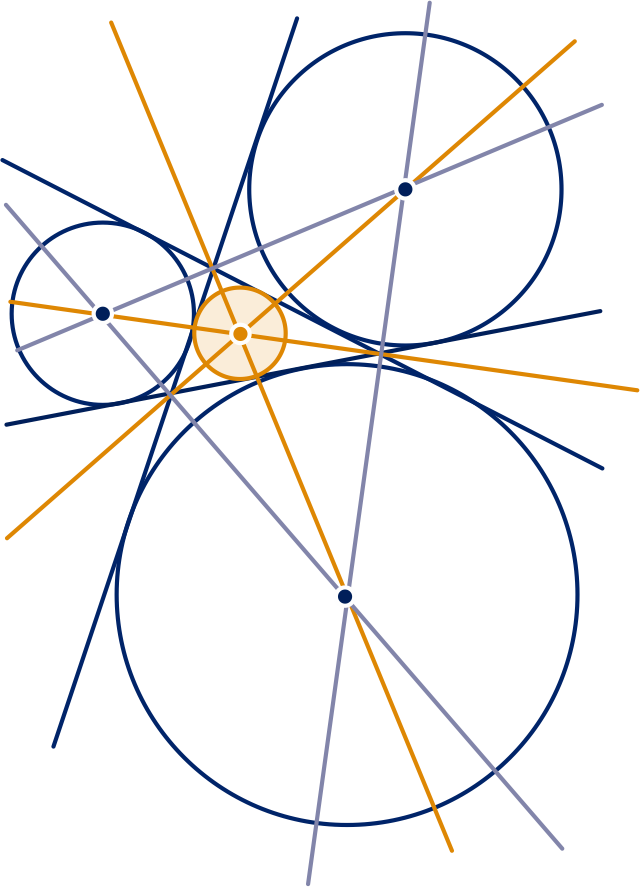
Het middelpunt van de cirkels is $M$ . Merk op dat het middelpunt bij een stomphoekige driehoek buiten de driehoek ligt.

8

a

Zie de figuur bij de stelling.
De driehoeken $S P Q$ en $S P R$ zijn congruent (HZH), want de hoeken $Q S P$ en $R S P$ zijn gelijk evenals de hoeken $S Q P$ en $S R P$ (recht).
De zijde $S P$ hebben ze gemeenschappelijk.
Dus: $d (P, lijn S Q) = | P Q | = | P R | = d (P, lijn S R)$ .

b

Gegeven is een driehoek $A B C$ .
Noem het snijpunt van de bissectrices van de hoeken $A$ en $B$ : $S$ .
$d (S, A B) = d (S, A C)$ , want $S$ ligt op de bissectrice van hoek $A$ .
$d (S, A B) = d (S, B C)$ , want $S$ ligt op de bissectrice van hoek $B$ .
Hieruit volgt dat $d (S, A C) = d (S, B C)$ .
Dus $S$ ligt op de bissectrice van hoek $C$ .
Dus gaan de bissectrices van de hoeken $A$ , $B$ en $C$ door één punt (namelijk door het punt $S$ ).

9

Noem de hoekpunten van de driehoek $A$ , $B$ en $C$ . Het het snijpunt $S$ van de bissectrices ligt even ver van de zijden van driehoek $A B C$ .
Noem die gelijke afstand $r$ . De cirkel met middelpunt $S$ en straal $r$ raakt aan de zijden $A B$ , $B C$ en $C A$ .

10

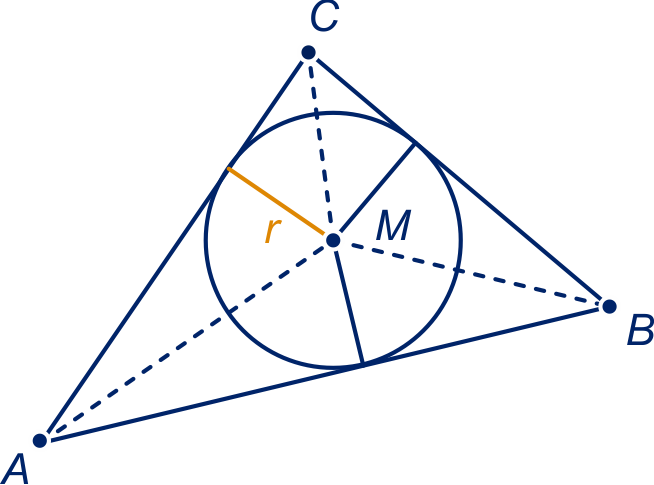
De stippellijnen zijn de bissectrices van de hoeken.

11

Gegeven is een driehoek $A B C$ .
Noem het snijpunt van de buitenbissectrices van de hoeken $A$ en $B$ : $S$ .
$d (A C, S) = d (A B, S)$ , want $S$ ligt op de buitenbissectrice van hoek $A$ .
$d (A B, S) = d (B C, S)$ , want $S$ ligt op de buitenbissectrice van hoek $B$ .
Hieruit volgt dat $d (A C, S) = d (B C, S)$ .
Dus $S$ ligt op de bissectrice van hoek $C$ .
Dus gaan de buitenbissectrices van de hoeken $A$ en $B$ en de bissectrice van hoek $C$ door één punt (namelijk door het punt $S$ ).

12

figuur bij opgave 28

13

a

Uit de stelling van Pythagoras volgt: $| A X |^{2} - a^{2} = | Y X |^{2} = | B X |^{2} - b^{2}$ , dus $| A X |^{2} - a^{2} = | B X |^{2} - b^{2}$ .

b

De verzameling punten $X$ waarvoor $| A X |^{2} - | B X |^{2} = 8$ is de lijn door $Y$ , loodrecht op $A B$ .

14

$| H B |^{2} - | H C |^{2} = | A B |^{2} - | A C |^{2}$ , want de lijn $A H$ staat loodrecht op $B C$ .
$| H A |^{2} - | H C |^{2} =$ $| B A |^{2} - | B C |^{2}$ , want de lijn $B H$ staat loodrecht op $A C$ .
Hieruit volgt dat $| H B |^{2} - | H A |^{2} =$ $| C B |^{2} - | C A |^{2}$ .
Dus staat de lijn $C H$ loodrecht op $A B$ en dus is lijn $H C$ ook hoogtelijn in driehoek $A B C$ .

15

Noem het snijpunt van $a$ en $b$ : $S$ .
$| S M_{2} |^{2} - | S M_{3} |^{2} = r_{2}^{2} - r_{3}^{2}$ , want $S$ ligt op $a$ en $a$ staat loodrecht op $M_{2} M_{3}$ .
$| S M_{1} |^{2} - | S M_{3} |^{2} =$ $r_{1}^{2} - r_{3}^{2}$ , want $S$ ligt op $b$ en $b$ staat loodrecht op $M_{1} M_{3}$ .
Hieruit volgt dat $| S M_{2} |^{2} - | S M_{1} |^{2} =$ $r_{2}^{2} - r_{1}^{2}$ .
$| X M_{2} |^{2} - | X M_{1} |^{2} = r_{2}^{2} - r_{1}^{2}$ geldt alleen voor punten $X$ op $c$ . Dus ligt $S$ ook op $c$ .
Dus gaan $a$ , $b$ en $c$ door één punt (namelijk het punt $S$ ).

16

Te bewijzen dat drie lijnen - zeg $a$ , $b$ en $c$ - door één punt gaan.
Noem het snijpunt van $a$ en $b$ : $S$ .
Voor $S$ geldt .... , want $S$ ligt op $a$ .
Voor $S$ geldt .... , want $S$ ligt op $b$ .
Hieruit volgt (met de twee eigenschappen wordt een berekening uitgevoerd): voor $S$ geldt ....