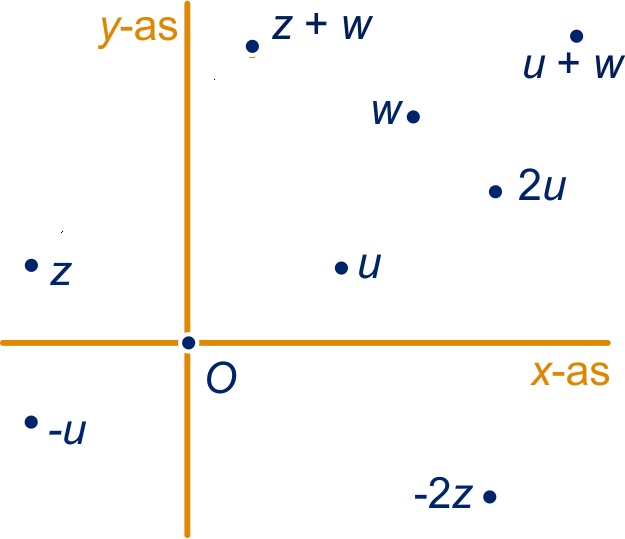
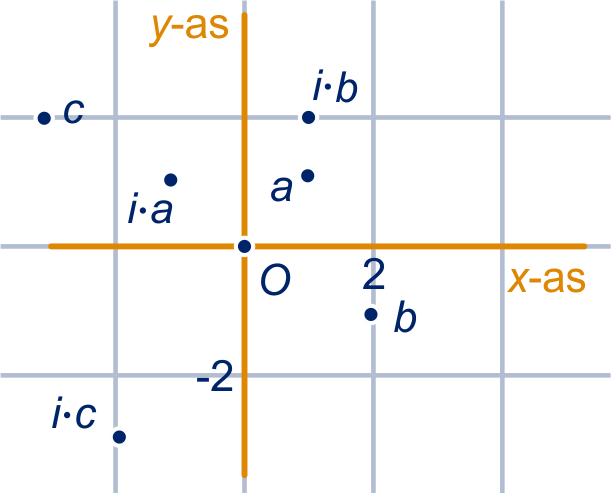
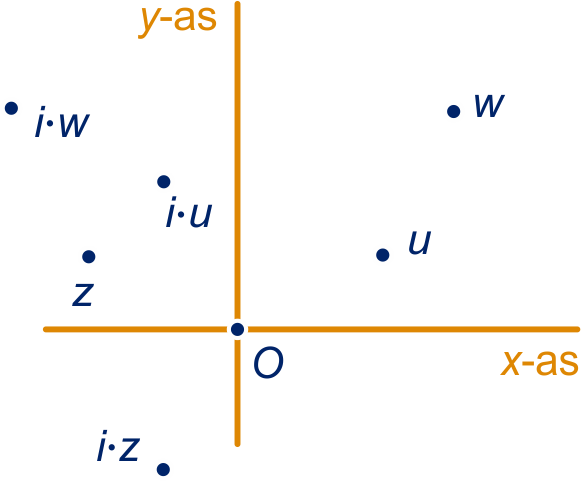
Als $z=a+bi$, dan $iz=\mathrm{‐}b+ai$, dus het punt $\left(a,b\right)$ wordt afgebeeld op $(\mathrm{‐}b,a)$. In paragraaf 5.6 van 4vb staat dat dit neerkomt op het linksom draaien om $O$ over $90°$.

$1\frac{1}{4}\text{π}$; de afstand is $\sqrt{2^2+2^2}=2\sqrt{2}$.

Voor $w$: $\text{ϕ}=1\frac{2}{3}\text{π}$ en de afstand is $\sqrt{1^2+{\sqrt{3}}^2}=2$.
Voor $u$: $\text{ϕ}=\text{π}$ en de afstand is $10$.

Die hoek is $\text{ϕ}=2\text{π}-\text{α}$, waarbij $\text{tan}\left(\text{α}\right)=1\frac{1}{2}$; je vindt: $\text{ϕ}=\mathrm{5,3}$.

Dit volgt meteen uit het feit dat $a=r\cdot \cos \left(\text{ϕ}\right)$ en $b=r\cdot \sin \left(\text{ϕ}\right)$ als $z$ correspondeert met $\left(a,b\right)$.

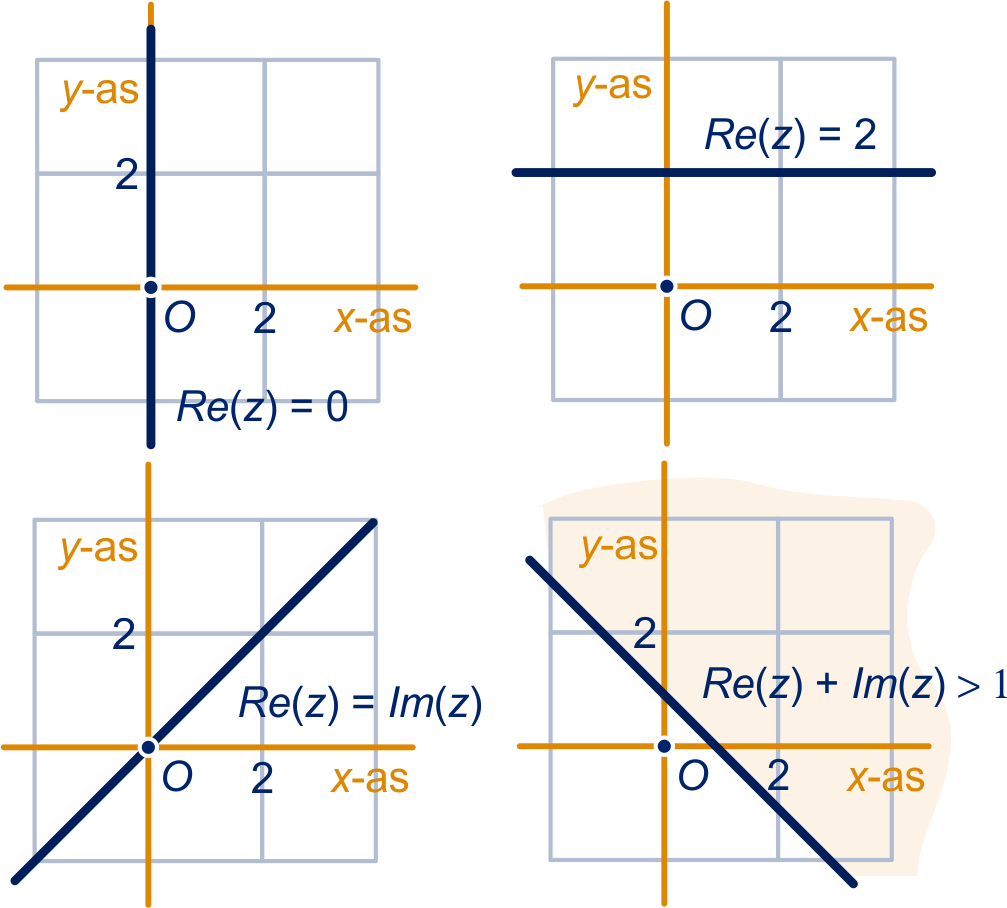
De punten $z$ met: $\arg \left(z\right)=\frac{3}{4}\text{π}$ vormen de eenheidscirkel.
De punten $z$ met: $\left|z\right|=1$ liggenop de halve lijn met beginpunt $0$ die door $\mathrm{‐}1+i$ gaat.

$0<z\le 4$, dus $0<\arg \left(z\right)\le \text{2π}$. De snijpunten met de assen en de lijnen $y=x$ en $y=\mathrm{‐}x$ hebben de eigenschap dat $\arg \left(z\right)=k\cdot \frac{1}{4}\text{π}$ met $k$ geheel, nu dus $k=\mathrm{1,}\mathrm{2,}\dots ,8$.
Je vindt: $z=\frac{1}{4}\sqrt{2}+\frac{1}{4}i\sqrt{2}$, $z=i$, $z=\mathrm{‐}\frac{3}{4}\sqrt{2}+\frac{3}{4}i\sqrt{2}$, $z=\mathrm{‐}2$, $z=\mathrm{‐}1\frac{1}{4}\sqrt{2}-1\frac{1}{4}i\sqrt{2}$, $z=\mathrm{‐}3i$, $z=1\frac{3}{4}\sqrt{2}-1\frac{3}{4}i\sqrt{2}$ en $z=4$.

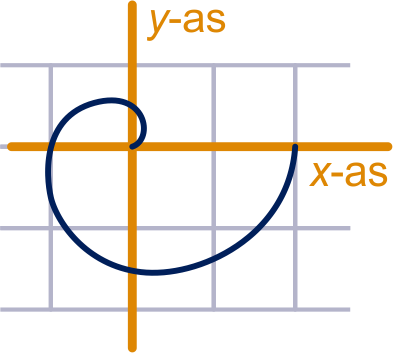
Neem $t=\left|z\right|$ als parameter, dan $\text{ϕ}=\frac{1}{2}\text{π}t$ en
$\left(x,y\right)=\left(t\cdot \cos \left(\frac{1}{2}\text{π}t\right),t\cdot \sin \left(\frac{1}{2}\text{π}t\right)\right)$.

-

Uit de somformules volgt:
$\cos \left(\text{α}\right)\cos \left(\text{β}\right)-\sin \left(\text{α}\right)\sin \left(\text{β}\right)+i\cdot \sin \left(\text{α}\right)\cos \left(\text{β}\right)+i\cdot \cos \left(\text{α}\right)\sin \left(\text{β}\right)=$
$\cos \left(\text{α}+\text{β}\right)+\sin \left(\text{α}+\text{β}\right)\cdot i$, dus $z\cdot w=$ $rs\cdot \left(\cos \left(\text{α}+\text{β}\right)+\sin \left(\text{α}+\text{β}\right)\cdot i\right)$.

Als je twee getallen met absolute waarde $1$ vermenigvuldigt is de absolute waarde van het product ook $1$. Dit volgt uit stelling 1.1.

$\left|z^2\right|={\left|z\right|}^2$, dit volgt ook uit stelling 1.1.

$\arg \left(z^2\right)=2\cdot \arg \left(z\right)$ op een veelvoud van $2\text{π}$ na. Dit volgt direct uit stelling 1.2.

Dan is $z$ unitair, dit volgt direct uit stelling 1.1.

In het eerste geval geldt: $\left|z\right|=z$, dus $\mathrm{Im}\left(z\right)=0$ en $\mathrm{Re}\left(z\right)\ge 0$.
In het tweede geval geldt: $\left|z\right|=\mathrm{‐}z$, dus $\mathrm{Im}\left(z\right)=0$ en $\mathrm{Re}\left(z\right)\le 0$.

$\arg \left(i\right)=\frac{1}{2}\text{π}$, dus $\arg \left(iz\right)=\arg \left(z\right)+\frac{1}{2}\text{π}$ op een veelvoud van $2\text{π}$ na.
$\left|i\right|=1$, dus $\left|iz\right|=\left|z\right|$.
Dus $iz$ ligt op dezelfde cirkel met middelpunt $0$ en de hoek met de positieve reële as is $\frac{1}{2}\text{π}$ groter.

Uit stelling 1.1 volgt dat ${\left|z\right|}^3=1$, dus $\left|z\right|=1$.

$\arg \left(1\right)=0$, dus $\arg \left(z^3\right)=3\cdot \arg \left(z\right)=0$ op een veelvoud van $2\text{π}$ na.

$z=1$, $z=\cos \left(\frac{2}{3}\text{π}\right)+i\cdot \sin \left(\frac{2}{3}\text{π}\right)$ $=\mathrm{‐}\frac{1}{2}+\frac{1}{2}i\sqrt{3}$, $z=\cos \left(\frac{4}{3}\text{π}\right)+i\cdot \sin \left(\frac{4}{3}\text{π}\right)$$=$ $\mathrm{‐}\frac{1}{2}-\frac{1}{2}i\sqrt{3}$.

Er geldt $\left|z\right|=1$ en $4\cdot \arg \left(z\right)=0$ op een veelvoud van $2\text{π}$ na. Voor de tekening, zie figuur 1 hieronder.
De oplossingen zijn: $z=1$, $z=i$, $z=\mathrm{‐}1$, $z=\mathrm{‐}i$

Er geldt $\left|z\right|=1$ en $8\cdot \arg \left(z\right)=0$ op een veelvoud van $2\text{π}$ na. Voor de tekening, zie figuur 2 hieronder.
De oplossingen zijn:
$z=1$, $z=\frac{1}{2}\sqrt{2}+\frac{1}{2}i\sqrt{2}$, $z=i$, $z=\mathrm{‐}\frac{1}{2}\sqrt{2}+\frac{1}{2}i\sqrt{2}$, $z=\mathrm{‐}1$, $z=\mathrm{‐}\frac{1}{2}\sqrt{2}-\frac{1}{2}i\sqrt{2}$, $z=\mathrm{‐}i$, $z=\frac{1}{2}\sqrt{2}-\frac{1}{2}i\sqrt{2}$.

Zie figuur 3 hieronder.

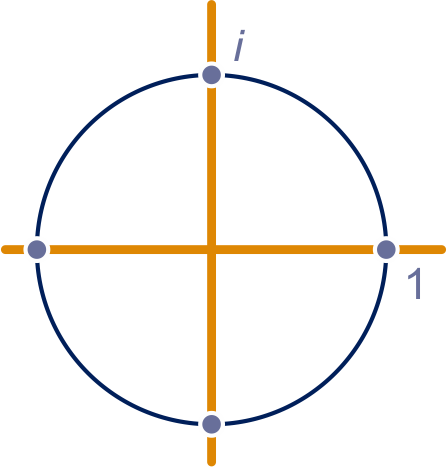
figuur 1 opgave 23

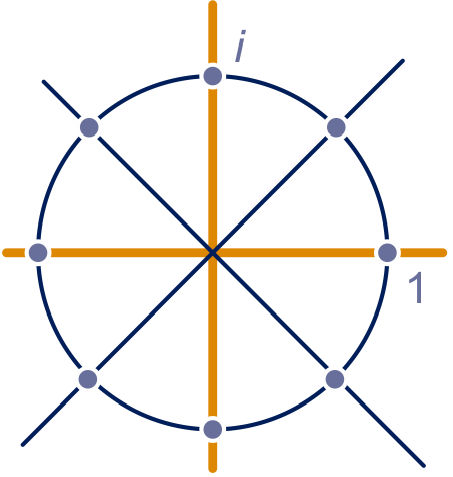
figuur 2 opgave 23

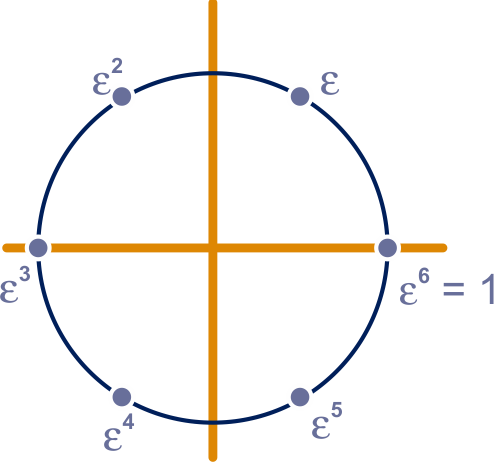
figuur 3 opgave 24

$\text{ε}=\frac{1}{2}+\frac{1}{2}i\sqrt{3}$

Draaien over $60°$ in tegenwijzerrichting om $0$.

${\text{ε}}^2$, ${\text{ε}}^3$, ${\text{ε}}^4$, ${\text{ε}}^5$, ${\text{ε}}^6=1$.

$\text{ε}+{\text{ε}}^5=1$, ${\text{ε}}^2+{\text{ε}}^4=\mathrm{‐}1$, dus $\text{ε}+{\text{ε}}^2+{\text{ε}}^3+{\text{ε}}^4+{\text{ε}}^5=\mathrm{‐}1+1+\mathrm{‐}1=\mathrm{‐}1$.
Of: $\text{ε}+{\text{ε}}^2+{\text{ε}}^3+{\text{ε}}^4+{\text{ε}}^5+{\text{ε}}^6=0$, dus $\text{ε}+{\text{ε}}^2+{\text{ε}}^3+{\text{ε}}^4+{\text{ε}}^5=\mathrm{‐}{\epsilon }^6=\mathrm{‐}1$.

Zie de figuur in onderdeel a. $\mathrm{‐}\text{ε}={\text{ε}}^4$ en ${\text{ε}}^2+1=\text{ε}$.

Zie figuur. Dat is de afstand van ${\text{ε}}^2$ tot $1$, dus de lengte van de 'basis' van een gelijkbenige driehoek met tophoek $120°$ en twee zijden van lengte $1$. Dus $\sqrt{3}$.

$\arg \left(\mathrm{‐}1\right)=\text{π}$, dus $8\cdot \arg \left(z\right)=\text{π}$ op een veelvoud van $2\text{π}$ na.

Er geldt $\left|z\right|=1$ en $\arg \left(z\right)=\frac{1}{8}\text{π}+k\cdot \frac{1}{4}\text{π}$, met $k$ geheel. Dus de oplossingen zijn: $\cos \left(\frac{1}{8}\text{π}+k\cdot \frac{1}{4}\text{π}\right)+i\cdot \sin \left(\frac{1}{8}\text{π}+k\cdot \frac{1}{4}\text{π}\right)$, met $k=\mathrm{0,}\mathrm{1,}\dots \mathrm{,7}$.

$3\cdot \arg \left(z\right)=\text{π}$ op een veelvoud van $2\text{π}$ na. Dus $\arg \left(z\right)=\frac{1}{3}\text{π}$, $\arg \left(z\right)=\text{π}$ of $\arg \left(z\right)=\mathrm{‐}\frac{1}{3}\text{π}$.

${\left|z\right|}^3=8$, dus $\left|z\right|=2$.

$z=2\cdot \cos \left(\frac{1}{3}\text{π}+k\cdot \frac{2}{3}\text{π}\right)+2i\cdot \sin \left(\frac{1}{3}\text{π}+k\cdot \frac{2}{3}\text{π}\right)$ met $k$ geheel, dus $z=1+i\sqrt{3}$, $z=\mathrm{‐}1$, $z=1-i\sqrt{3}$.
Je kunt ook ook zeggen: je krijgt de oplossingen door die van $z^3=1$ met $\mathrm{‐}2$ te vermenigvuldigen.

$3\cdot \arg \left(z\right)=\arg \left(i\right)=\frac{1}{2}\text{π}$ op een veelvoud van $2\text{π}$ na, dus $\arg \left(z\right)=\frac{1}{6}\text{π}+k\cdot \frac{2}{3}\text{π}$. Dus $z=\cos \left(\frac{1}{6}\text{π}+k\cdot \frac{2}{3}\text{π}\right)+i\cdot \sin \left(\frac{1}{6}\text{π}+k\cdot \frac{2}{3}\text{π}\right)$. Je vindt: $z=\frac{1}{2}\sqrt{3}+\frac{1}{2}i$, $z=\mathrm{‐}\frac{1}{2}\sqrt{3}+\frac{1}{2}i$ en $z=\mathrm{‐}i$.

$3\cdot \arg \left(z\right)=\arg \left(\mathrm{‐}i\right)=\mathrm{‐}\frac{1}{2}\text{π}$ op een veelvoud van $2\text{π}$ na, dus $\arg \left(z\right)=\frac{1}{6}\text{π}+k\cdot \frac{2}{3}\text{π}$. Dus $z=\cos \left(\mathrm{‐}\frac{1}{6}\text{π}+k\cdot \frac{2}{3}\text{π}\right)+i\cdot \sin \left(\mathrm{‐}\frac{1}{6}\text{π}+k\cdot \frac{2}{3}\text{π}\right)$. Je vindt: $z=\frac{1}{2}\sqrt{3}\mathrm{-}\frac{1}{2}i$, $z=\mathrm{‐}\frac{1}{2}\sqrt{3}\mathrm{-}\frac{1}{2}i$ en $z=i$.
Je kunt ook zeggen: het zijn de tegengestelden van de oplossingen uit a.

$3\cdot \arg \left(z\right)=\arg \left(2+2i\right)=\frac{1}{4}\text{π}$ op een veelvoud van $2\text{π}$ na, dus $\arg \left(z\right)=\frac{1}{12}\text{π}$, $\arg \left(z\right)=\frac{3}{4}\text{π}$ of $\arg \left(z\right)=\mathrm{‐}\frac{7}{12}\text{π}$.
${\left|z\right|}^3=\left|2+2i\right|=\sqrt{8}$, dus $\left|z\right|=\sqrt{2}$.

$z=\sqrt{2}\cdot \cos \left(\frac{3}{4}\text{π}\right)+i\sqrt{2}\cdot \sin \left(\frac{3}{4}\text{π}\right)=\mathrm{‐}1+i$

$3\cdot \arg \left(z\right)=\arg \left(2-2i\right)=\mathrm{‐}\frac{1}{4}\text{π}$ op een veelvoud van $2\text{π}$ na, dus $\arg \left(z\right)=\mathrm{‐}\frac{1}{12}\text{π}$, $\arg \left(z\right)=\frac{7}{12}\text{π}$ of $\arg \left(z\right)=1\frac{1}{4}\text{π}$ (ofwel $\mathrm{‐}\frac{3}{4}\text{π}$).
De oplossing is: $\sqrt{2}\cdot \cos \left(\mathrm{‐}\frac{3}{4}\text{π}\right)+i\sqrt{2}\cdot \sin \left(\mathrm{‐}\frac{3}{4}\text{π}\right)=\mathrm{‐}1-i$.