,
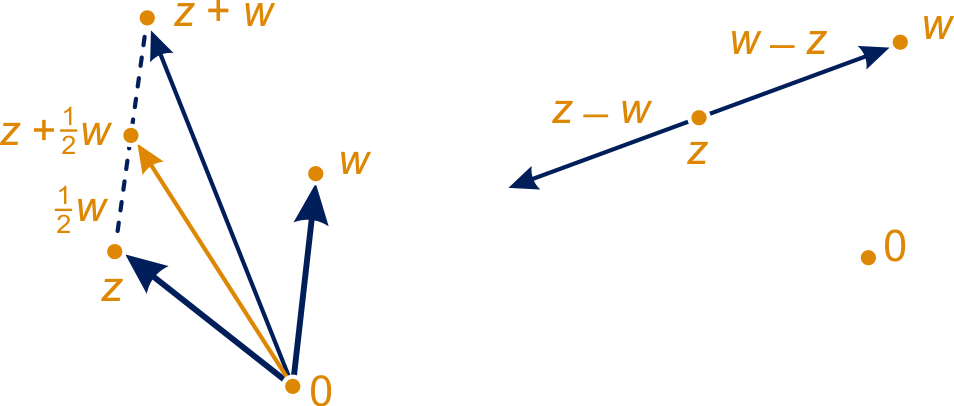
Ze vormen de lijn door en .
Ze vormen de lijn door en .
Die getallen vormen het lijnstuk met eindpunten en .
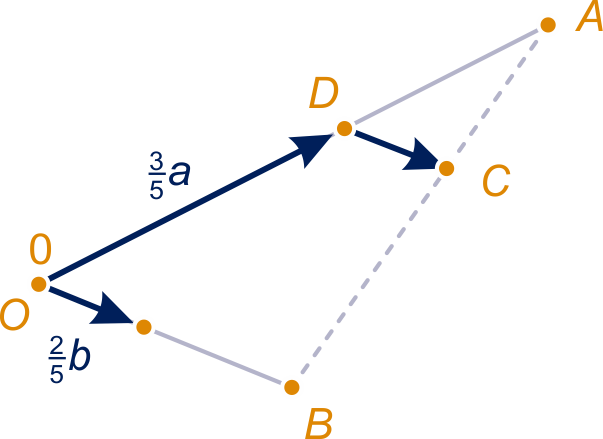
Het punt bij noemen we .
Dan zijn de driehoeken en
gelijkvormig, dus
.
Dit volgt uit bovenstaande stelling met , , en .
Omdat symmetrisch in , en is.
Uit onderdeel b van deze opgave en onderdeel h van
opgave 42 volgt:
.
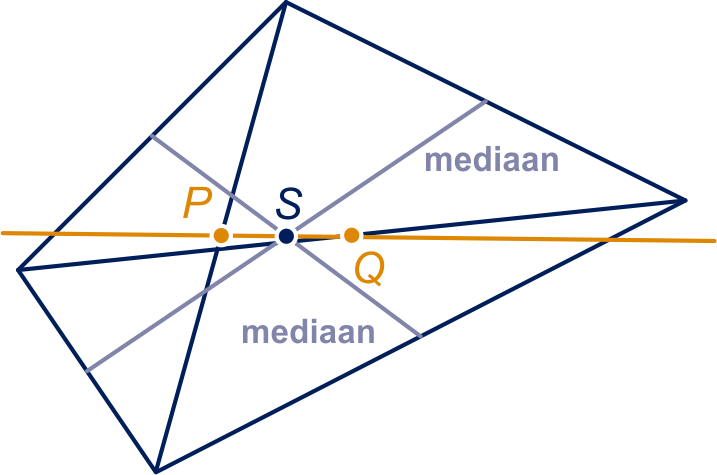
en zijn middens van diagonalen; is het snijpunt van de medianen.
Noem de hoekpunten van de vierhoek , ,
en en de bijbehorende complexe getallen
, ,
en .
Bij het midden van hoort
het complexe getal .
Bij het midden van hoort
het complexe getal .
Het midden van en ligt op mediaan . Het complexe getal dat hierbij
hoort is: .
Vanwege de symmetrie in deze uitdrukking ligt dit punt ook op de andere mediaan.
Het getal dat bij het midden van hoort is
en bij het midden van
: .
Het getal bij het midden van
is . Dit getal hoort bij het
snijpunt van de medianen.
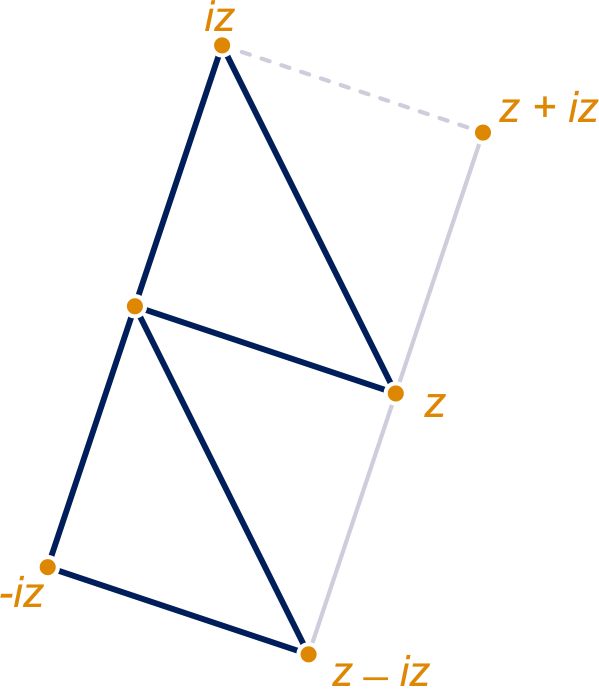
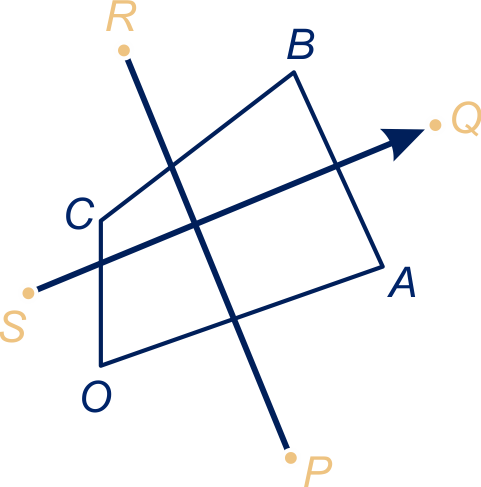
Een vierkant
Een vierkant
Eindpunt pijl 1: ; eindpunt pijl 2: .
en ,
Klopt
krijg je door een kwartslag tegen de wijzers van de klok in te draaien. Dus en zijn even lang en staan loodrecht op elkaar.
Zet op de zijden van een parallellogram vierkanten. De middens van die vierkanten zijn hoekpunten van een vierkant.
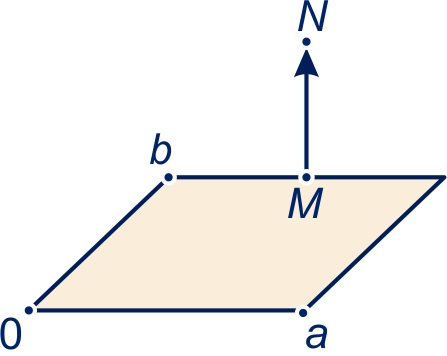
is het midden van een zijde van het parallellogram en
het midden van van een vierkant op de zijden.
Dan en
, dus
.
De middens van de vierkanten op de zijden van het parallellogram vanaf
met de klok mee noemen we ,
en .
Dan ,
en
.
Uit onderdeel c volgt:
,
,
en
.
Dus:
, ,
,
.
Hieruit volgt: bij draaiing over een kwartslag in wijzerrichting is
lijnstuk het beeld van lijnstuk ,
lijnstuk het beeld van lijnstuk ,
lijnstuk het beeld van lijnstuk .
Dus is een vierkant.
is het midden van
zijde . Dan
en
, dus
.
Op soortgelijke wijze vind je:
,
en
.
en
Er geldt: , dus lijnstuk krijg je uit lijnstuk door een kwartslag linksom te draaiien.
Het hoekpunt
tegenover
hoort bij ;
het
hoekpunt tegenover bij
.
Dan , onafhankelijk van
.
-
Het punt in het vlak bij noemen we D. Dan is een ruit omdat . Het gevraagde volgt uit het feit dat de diagonalen in een ruit loodrecht op elkaar staan.
representeert , dus uit onderdeel a volgt dat loodrecht op staat.
Omdat de formule voor symmetrisch is in , en , is het hoogtepunt van driehoek .
De punten bij , en liggen op één lijn en .
Noem de hoogtepunten van de vier driehoeken achtereenvolgens
,
,
en
.
In opgave 50 hebben we bewezen:
,
,
en
.
Uit onderdeel a volgt: , dus is evenwijdig met en even lang als enzovoort.
Noem de zwaartepunten van de vier driehoeken achtereenvolgens
,
,
en
.
Dan is
, ,
,
en
.
Dan , dus
is evenwijdig met
en de lengte van
is
van de lengte van
enzovoort.
en , dus vermenigvuldigen met is linksom draaien over . Bovendien geldt: voor elke postitieve gehele waarde van .
Rechtsom draaien over .
is het spiegelbeeld van in de imaginaire as, dus en dus .
en .
Zie figuur 1 hieronder.
Het is een regelmatige driehoek .
Zie figuur 2. of .
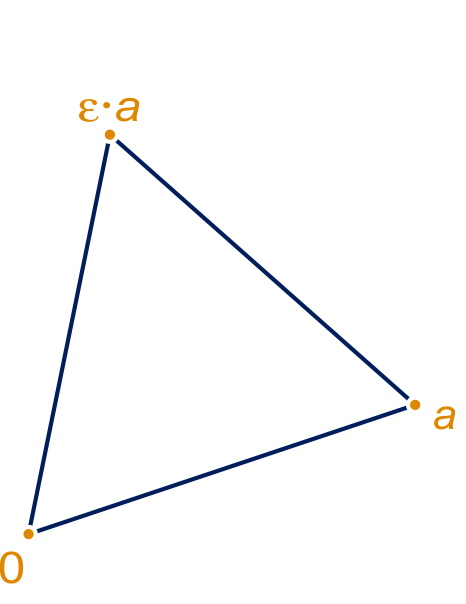
figuur 1
|
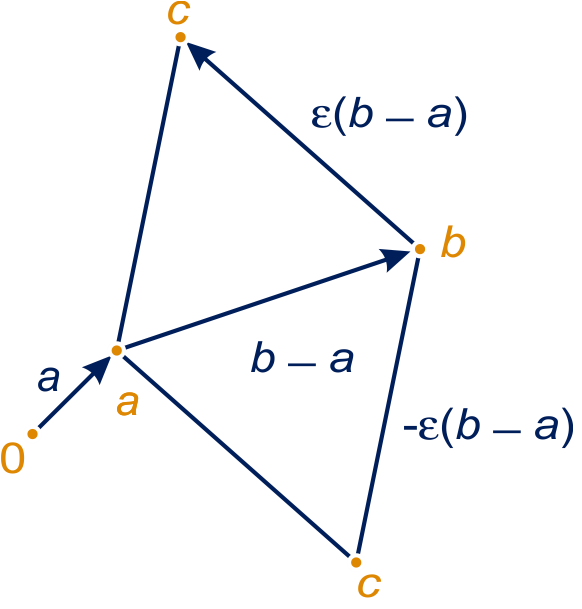
figuur 2
|
We kiezen de oorsprong van het complexe vlak in . Da: en , dus .
We nemen het punt als oorsprong. Dan:
,
en
.
Verder:
,
en
.
We moeten aantonen dat:
.
Dit laatste volgt uit opgave 53c.
