Hoofdstukken > Inleiding complexe getallen

Rekenen met complexe getallen kent vele toepassingen. In veel gevallen werk je met complexe e-machten en moet je complex differentiëren. Wiskundig gezien is dit niet eenvoudig. Een toepassingsgebied waarbij je minder theorie over complexe getallen nodig hebt, is de meetkunde.
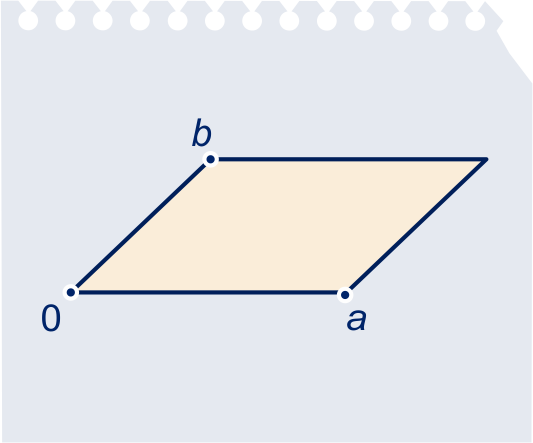
Eerst even het volgende. Af en toe komt het ons goed uit een complex getal als vector (pijl) te beschouwen.
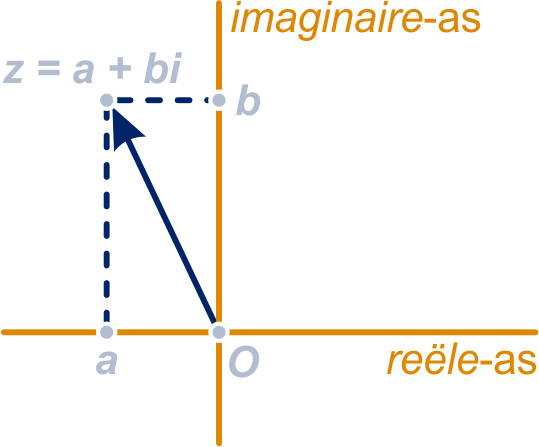
Het getal $z = a + b \cdot i$ (met $a$ en $b$ reëel, vatten we op als de vector die een verplaatsing van $a$ eenheden in de ‘reële’ richting en $b$ eenheden in de ‘imaginaire’ richting aangeeft. (In de getekende situatie is $a$ negatief en $b$ postitief).

Wat we in de analytische meetkunde met vectoren, parametervoorstellingen enzovoort gedaan hebben, kunnen we kopiëren naar de complexe getallen.
In het vervolg kun je zien hoe dat gaat.

We noteren het punt horend bij het complexe getal $a$ met $A$ .

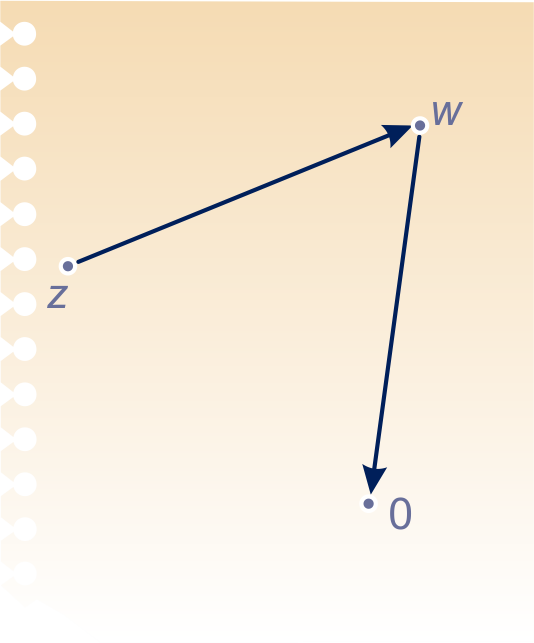
$z$ en $w$ zijn twee getallen in het complexe vlak.

Welk complex getal wordt voorgesteld door de vector die $z$ naar $w$ verplaatst? En die van $w$ naar $0$ wijst? Druk je antwoorden uit in $z$ en $w$ .

Neem het plaatje hiernaast over en teken hierin (als punten) de complexe getallen $z + w$ , $z - w$ , $w - z$ , $z + \frac{1}{2} w$ .

Druk het getal dat midden tussen $z$ en $w$ ligt uit in $z$ en $w$ .

Wat merk je op over de ligging van de complexe getallen $t \cdot w$ , waarbij $t$ alle mogelijke reële waarden aanneemt?

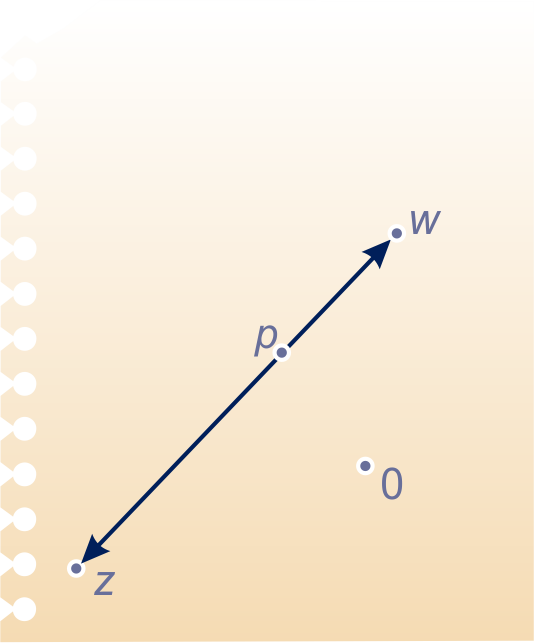
Het getal $p$ ligt op het verbindingslijnstuk van $z$ en $w$ zó, dat het twee keer zo ver van $z$ als van $w$ ligt, zie plaatje.

Druk $p$ uit in $z$ en $w$ .

We bekijken alle complexe getallen $z + t (w - z)$ , waarbij $t$ alle mogelijke reële waarden aanneemt.

Wat kun je zeggen over de ligging van die complexe getallen?

Wat kun je zeggen over de ligging als $0 \leq t \leq 1$ ?

Gegeven twee complexe getallen $a$ en $b$ .
Voor het getal $c$ geldt: $c = \frac{3}{5} a + \frac{2}{5} b$ . Dan ligt $C$ op lijnstuk $A B$ .

Bereken $A C : C B$ .

$z + t (w - z) = (1 - t) z + t w$ , dus uit de onderdelen f en g van opgave 42 volgt:

Stelling
Gegeven twee complexe getallen $z$ en $w$ .
De complexe getallen $s \cdot z + t \cdot w$ met $s$ en $t$ reëel en $s + t = 1$ vormen de lijn door $z$ en $w$ .
Voor $s \geq 0$ en $t \geq 0$ (en $s + t = 1$ ) krijg je de punten op het lijnstuk met eindpunten $z$ en $w$ .
We noemen $u = z + t (w - z)$ een parametervoorstelling (pv) van de lijn door $z$ en $w$ , dat wil zeggen:
als je voor $t$ alle mogelijke reële getallen neemt, dan vormen de complexe getallen $u$ precies de lijn door de punten $z$ en $w$ .
Een andere pv van de lijn door $z$ en $w$ is dus $u = s \cdot z + t \cdot w$ , met $s$ en $t$ reëel en $s + t = 1$ .

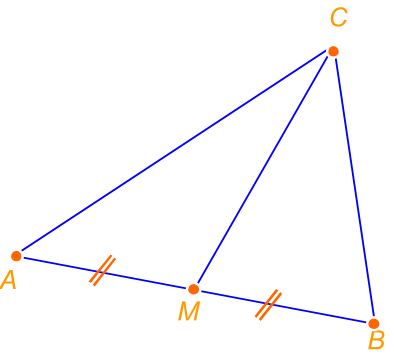
Een zwaartelijn in een driehoek is een lijn door een hoekpunt en het midden van de tegenoverliggende zijde.

In de figuur hiernaast is $M$ het midden van zijde $A B$ .
Lijn $C M$ is de zwaartelijn uit $C$ van driehoek $A B C$ .

Gegeven is een driehoek $A B C$ . De complexe getallen bij de hoekpunten van de driehoek zijn $a$ , $b$ en $c$ . Het midden van het verbindingslijnstuk van $A$ en $B$ is $M$ en het complexe getal dat bij $M$ hoort is $m$ .

Druk $m$ uit in $a$ en $b$ .

Toon aan dat $v = \frac{2}{3} \cdot \frac{1}{2} (a + b) + \frac{1}{3} c$ op de zwaartelijn vanuit $C$ ligt.

Schrijf $v$ zonder haakjes, zo eenvoudig mogelijk.

Hoe zie je met behulp van onderdeel c dat $v$ ook op de andere zwaartelijnen van driehoek $A B C$ ligt?

Het bij $v$ horende punt is $V$ .

Bereken $C V : V M$ .

We hebben nu de volgende stelling bewezen. (In vwo5 wiskunde b heb je deze stelling ook al bewezen.)

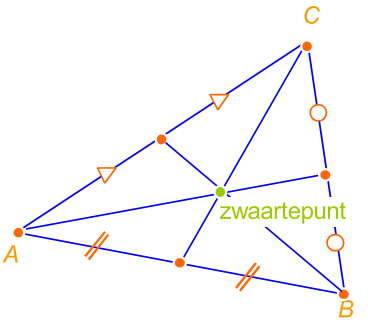
Stelling
De zwaartelijnen van een driehoek gaan door één punt. Dat punt heet het zwaartepunt van de driehoek. Het zwaartepunt ligt twee keer zo ver van een hoekpunt als van het midden van de tegenoverliggende zijde.

Teken een willekeurige vierhoek.
Teken het verbindingslijnstuk van de middens van de diagonalen van de vierhoek en de twee medianen van de vierhoek (een mediaan verbindt de middens van twee tegenover elkaar liggende zijden).

Het snijpunt van medianen ligt op het verbindingslijnstuk van de middens van de diagonalen.

Bewijs dat.

(hint)

Je kunt met complexe getallen bewijzen dat het midden van een mediaan ook op de andere mediaan ligt én op de verbindingslijn van de middens van de diagonalen.

Teken een getal $z$ in het complexe vlak. Teken hierbij het getal $i z$ en $z + i z$ .

Wat kun je zeggen over de vierhoek met hoekpunten: $0$ , $z$ , $i z$ en $z + i z$ ?

En wat kun je zeggen over de vierhoek met hoekpunten:

0

z

‐ i z

z - i z

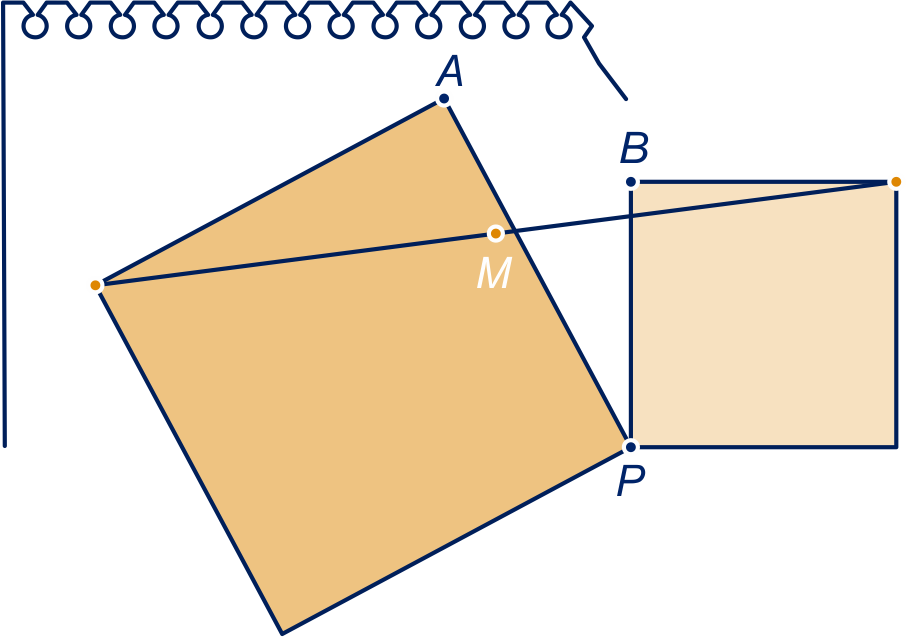
Hieronder links zijn twee vierkanten getekend met een gemeenschappelijk hoekpunt. Twee hoekpunten van het kleine vierkant zijn verbonden met twee hoekpunten van het grote vierkant, zie het plaatje hieronder.

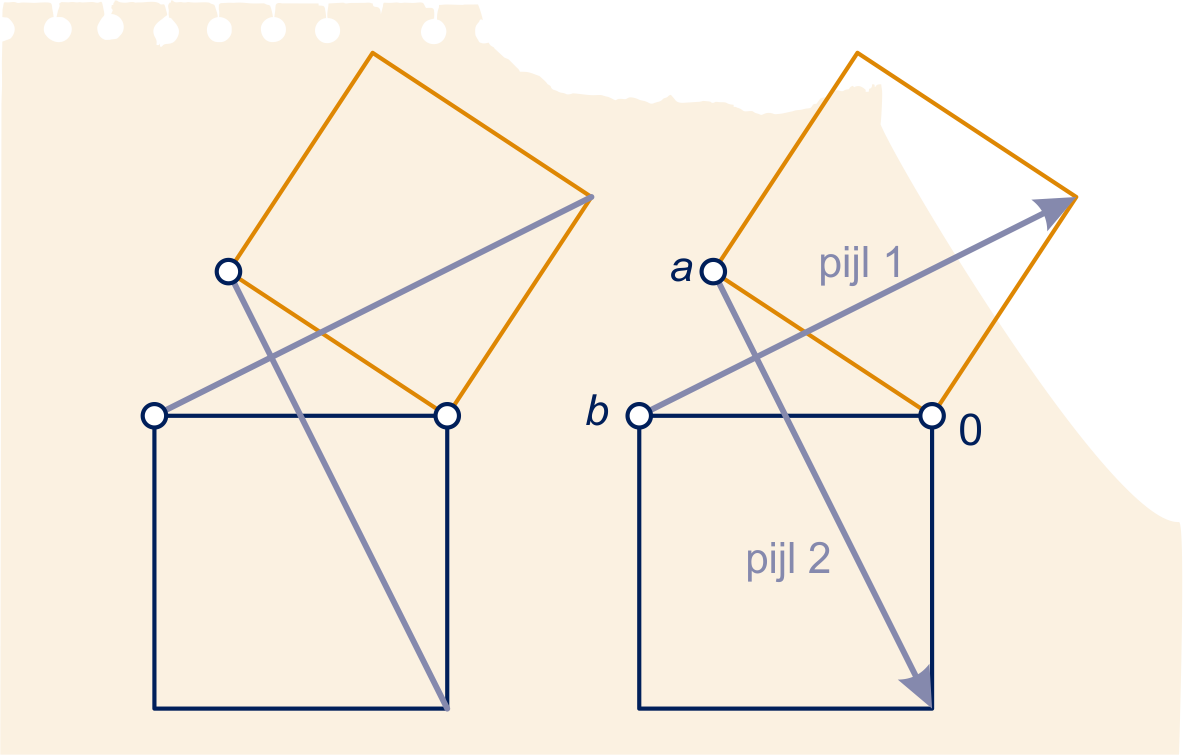
De verbindingslijnstukken zijn even lang en staan loodrecht op elkaar. Je kunt een bewijs geven met congruentie.
Het kan ook met complexe getallen. Dat gebeurt nu.
Kies het getal $0$ in het gemeenschappelijke hoekpunt van de vierkanten en de getallen $a$ en $b$ als in het plaatje hierboven rechts.

Druk de getallen bij de start- en eindpunten van de pijlen uit in $a$ en $b$ .

Welke getal $p$ hoort dus bij pijl 1? En welk getal $q$ bij pijl 2?

In de tekening kun je ‘zien’ dat $i q = p$ .

Reken na dat dat juist is.

Waarom heb je het bewijs nu gegeven?

Een Sangaku uit Pythagoras
In Pythagoras, jaargang 48, nummer 5 staat de volgende Sangaku op de achterkant.

De Sangaku is ontworpen door Hans van Lint, de winnaar van de NWD-sangakuwedstrijd 2009.
Een Sangaku beeldt zonder woorden een stelling uit. De kunst is om uit het diagram af te leiden welke stelling dat is en die te bewijzen.

Welke stelling?

Hiernaast is het parallellogram in het midden van de sangaku getekend. We kiezen de getallen $0$ , $a$ en $b$ als in het plaatje hiernaast.

Laat zien dat $b + \frac{1}{2} (a + a i)$ één van middens van de vierkanten op de zijden van het parallellogram is.

Druk de middens van de andere vierkanten ook in $a$ en $b$ uit.

Bewijs de stelling.

van Aubel

De stelling van Van Aubel
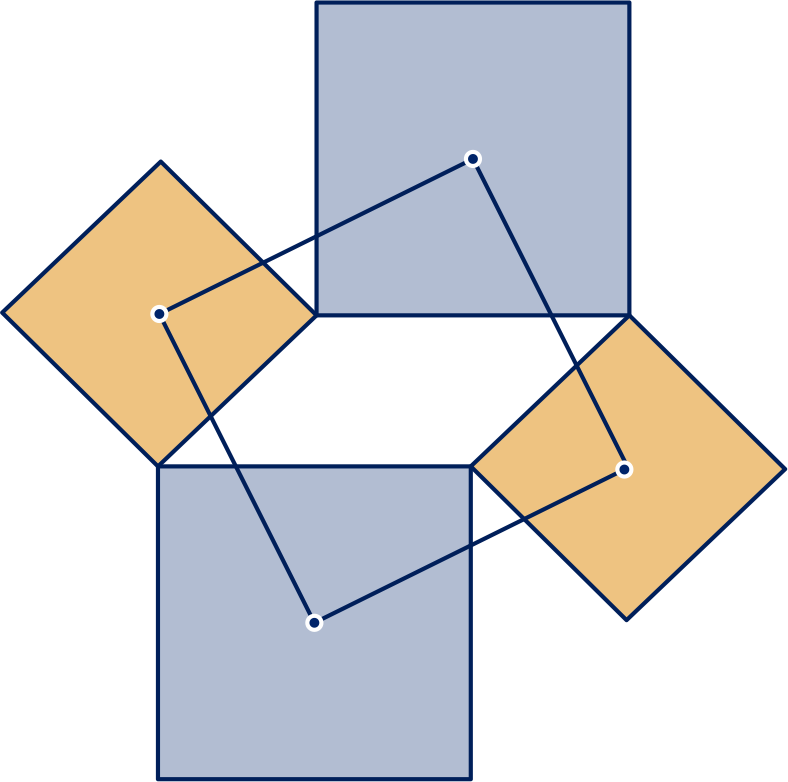
Op de zijden van een willekeurige vierhoek zijn vierkanten gezet. De middens van de vierkanten op tegenover elkaar liggende zijden worden met elkaar verbonden, zie plaatje.

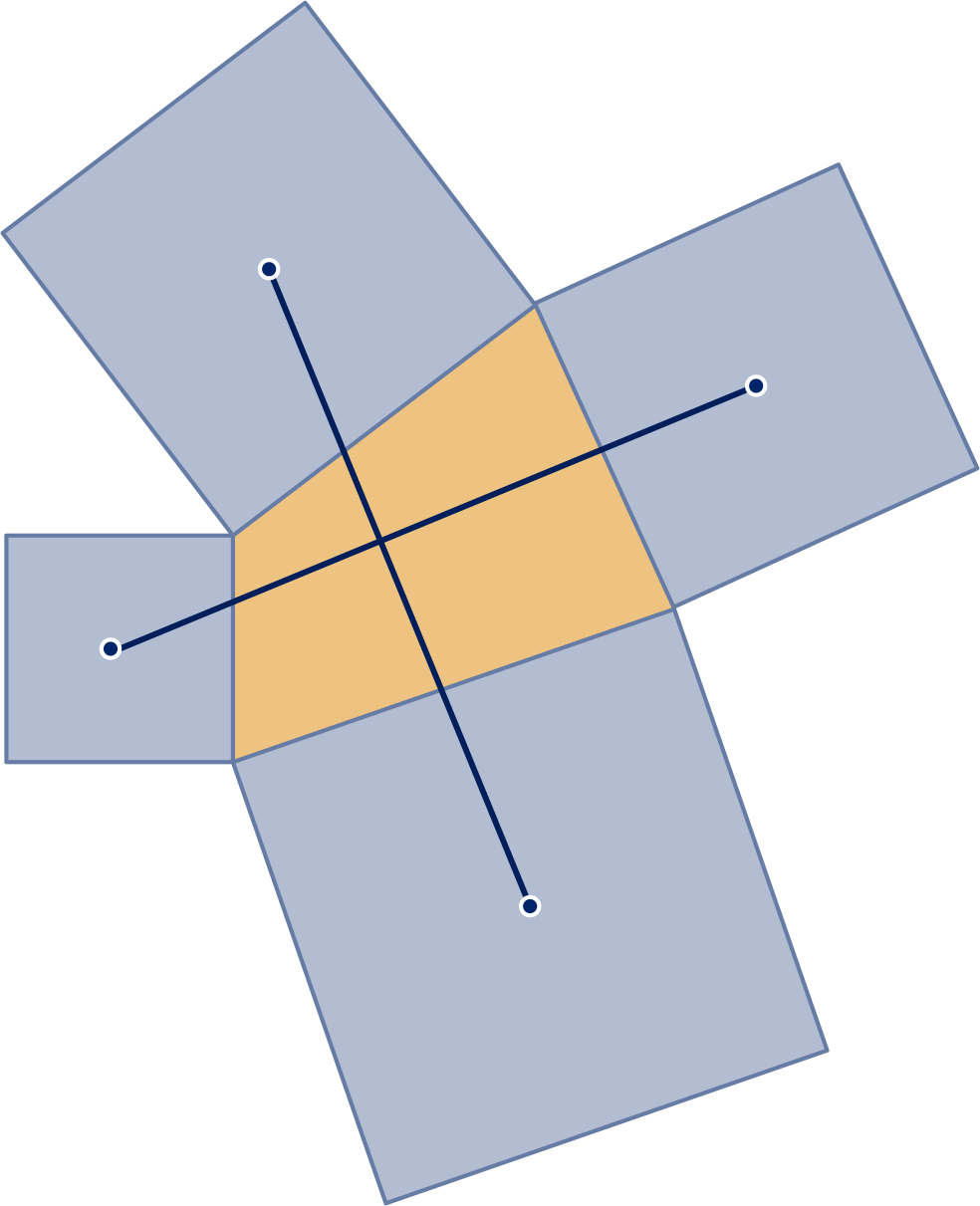
De verbindingslijnstukken zijn even lang en staan loodrecht op elkaar.
De stelling is genoemd naar Henricus Hubertus van Aubel (geboren op 20 november 1830 te Maastricht; overleden op 3 februari 1906 te Antwerpen), oa. leraar wiskunde aan het Koninklijk Atheneum van Antwerpen. Bron Wikipedia
We gaan de stelling bewijzen.
We geven de hoekpunten van de vierhoek en de middens van de vierkanten namen, zie het plaatje hiernaast.

Druk $p$ , $q$ , $r$ en $s$ in $a$ , $b$ , $c$ en $d$ .

(hint)

Bijvoorbeeld

q = \frac{1}{2} a + \frac{1}{2} c + \frac{1}{2} i a - \frac{1}{2} i c

Druk nu $r - p$ en $s - q$ uit in $a$ , $b$ , $c$ en $d$ .

Bewijs de stelling.

De stelling van Bottema
$A$ en $B$ zijn twee punten in het vlak. We kiezen een punt $P$ .
Op de lijnstukken $P A$ en $P B$ worden vierkanten gezet, zie plaatje.

Het hoekpunt tegenover $P$ van het ene vierkant wordt verbonden met het hoekpunt tegenover $P$ van het andere vierkant. Het midden van het verbindingslijnstuk noemen we $M$ .
De plaats van $M$ hangt niet van $P$ af.
Dit kun je mooi zien in een applet . Misschien kun je zo’n applet zelf wel maken.

Bewijs de stelling.

Definitie
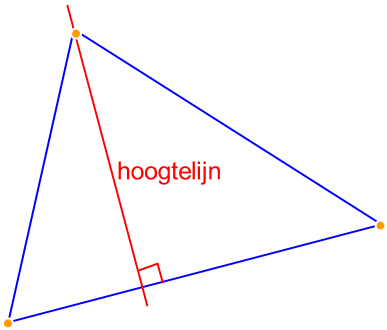
Een hoogtelijn van een driehoek gaat door een hoekpunt en staat loodrecht op de zijde tegenover dat hoekpunt.
De drie hoogtelijnen van een driehoek gaan door één punt. Dit punt heet het hoogtepunt van de driehoek.

De rechte van Euler

Teken een willekeurige driehoek, met het hoogtepunt, het zwaartepunt en het middelpunt van de omgeschreven cirkel van de driehoek.

Het lijkt wel of de drie punten op één lijn liggen. Dit gaan we in het volgende bewijzen. De lijn door de drie punten heet de rechte van Euler. Je kunt dit mooi zien in de volgende applet .
We kiezen het middelpunt van de omgeschreven cirkel als de oorsprong van het complexe vlak. Noem de hoekpunten van de driehoek $A$ , $B$ en $C$ .
Stel $h = a + b + c$ .

Waarom staat de verbindingslijn van $0$ met $a + b$ loodrecht op $A B$ ?

Leg uit dat hieruit volgt dat de lijn die $h$ met $c$ verbindt, loodrecht op $A B$ staat.

Hoe volgt nu dat $h$ bij het hoogtepunt van driehoek $A B C$ hoort?

Het hoogtepunt van driehoek $A B C$ noemen we $H$ en het zwaartepunt $Z$ .

Hoe volgt dat de punten $O$ , $Z$ en $H$ op een lijn liggen en dat $O Z : Z H = 1 : 2$ ?

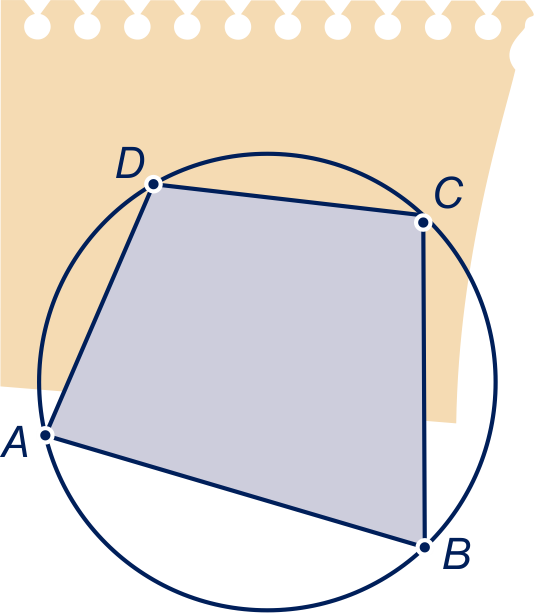
Gegeven is een koordenvierhoek $A B C D$ .
Dan is de vierhoek met als hoekpunten de hoogtepunten van de driehoeken $A B C$ , $A B D$ , $A C D$ en $B C D$ congruent met vierhoek $A B C D$ .

We bewijzen de stelling in deze opgave.
Als oorsprong $A B C D$ nemen we het middelpunt van de omgeschreven cirkel van de vierhoek.

Druk de complexe getallen bij die hoogtepunten uit in $a$ , $b$ , $c$ en $d$ .

(hint)

Gebruik opgave 50c.

Bewijs de stelling.

Stelling
Gegeven is een vierhoek $A B C D$ .
Dan vormen de zwaartepunten van de driehoeken $A B C$ , $A B D$ , $A C D$ en $B C D$ een vierhoek die gelijkvormig is met vierhoek $A B C D$ .

Bewijs de stelling en bepaal de bijbehorende vergrotingsfactor.

In de voorgaande bewijzen werd vaak gebruik gemaakt van de draaiing over $90 °$ , dus in de complexe getallen met de vermenigvuldiging met $i$ . In de laatste opgaven heb je de draaiing over $60 °$ nodig, dus vermenigvuldigen met $ε = \frac{1}{2} + \frac{1}{2} i \sqrt{3}$ , zie ook opgave 24.
Hierover gaat de volgende opgave, die voor een deel herhaling is.

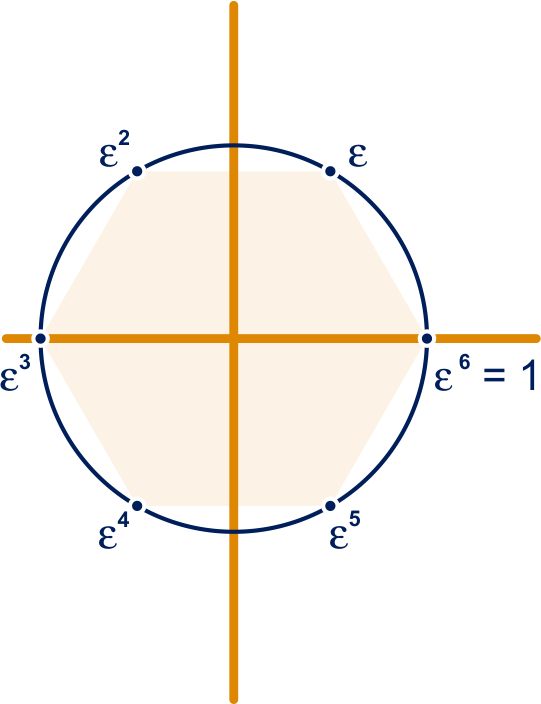
Gegeven het getal $ε = \frac{1}{2} + \frac{1}{2} i \sqrt{3}$ , zie opgave 24.

Laat zien de getallen $1$ , $ε^{2}$ , $ε^{3} = ‐ 1$ , $ε^{4}$ , $ε^{5}$ in het complexe vlak hoekpunten van een regelmatige zeshoek op de eenheidscirkel zijn.

Wat stelt vermenigvuldigen met $ε^{5}$ meetkundig voor?

Leg uit dat $ε^{2} + 1 = ε$ .

Druk $ε^{4}$ en $ε^{5}$ uit in $ε$ zonder machten van $ε$ te gebruiken.

$ε$ is als in opgave 53 en $a$ een willekeurig complex getal $\neq 0$ .

Teken de driehoek met hoekpunten $0$ , $a$ en $ε a$ .

Welke bijzonderheid heeft deze driehoek?

Welk punt krijg je als je $0$ spiegelt in de lijn door de punten $a$ en $ε a$ ? Druk je antwoord uit in $ε$ en $a$ .

Gegeven de getallen $a$ en $b$ . Er zijn twee getallen $c$ zodat driehoek $A B C$ gelijkzijdig is.

Druk $c$ uit in $a$ , $b$ en $ε$ .

De driehoeken $A B T$ en $C D T$ in de figuur hieronder zijn gelijkzijdig.

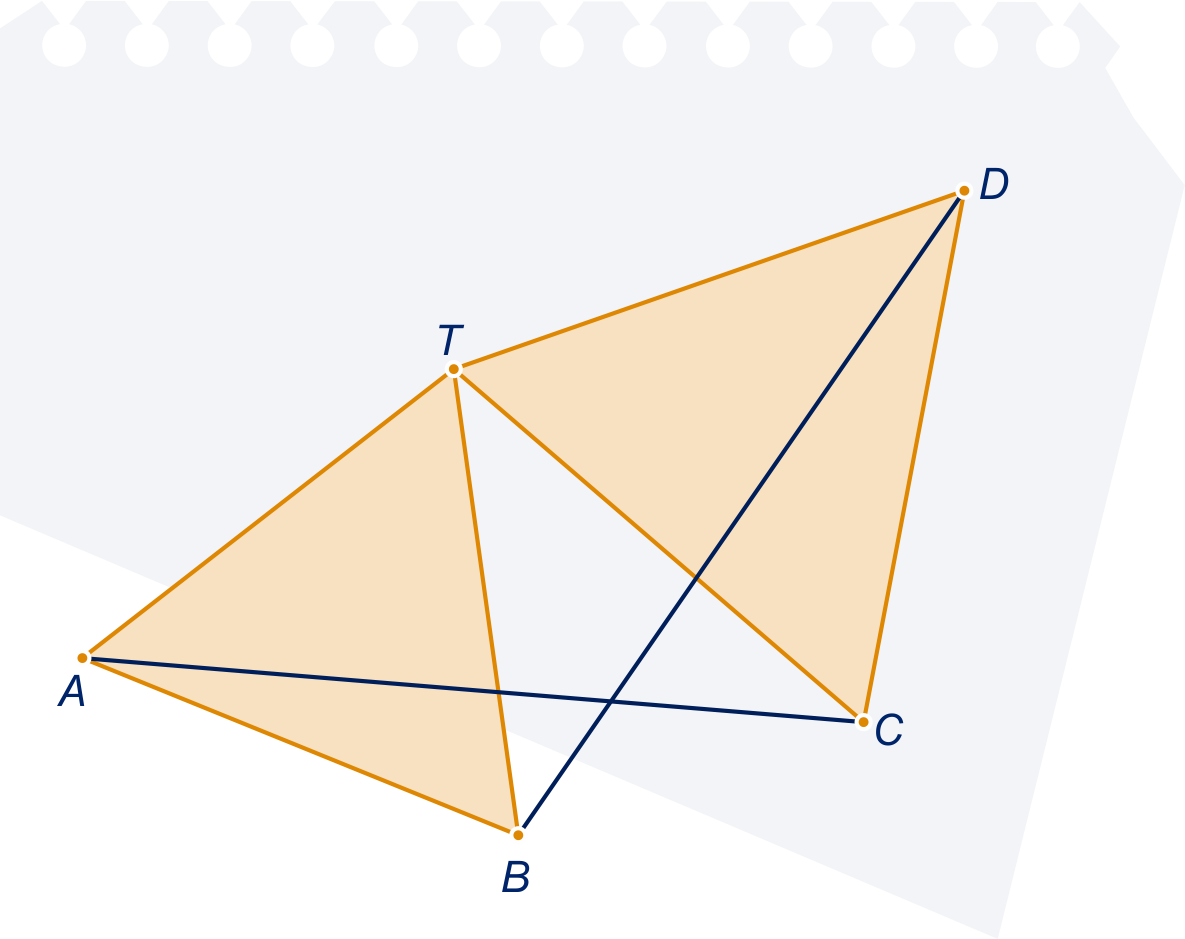
Toon met een berekening met complexe getallen aan: De lijnen $A C$ en $B D$ snijden elkaar onder een hoek van $60 °$ en de lijnstukken $A C$ en $B D$ zijn even lang.

Napoleon Bonaparte 1769-1821 Keizer der Fransen
Hij werd de machtigste man van Europa en een van de bekendste en meest invloedrijke figuren in de wereldgeschiedenis. Napoleon bleek als militair in opleiding uitzonderlijk goed te zijn in rekenen en kaartlezen. Het rekenen paste hij o.a. toe in de artillerie bij het berekenen van de baan van een kanonskogel, het kaartlezen gebruikte hij zijn leven lang om vanaf (vaak slordige en foute) kaarten een goede positie en opstelling na te streven.
Bron: Wikipedia

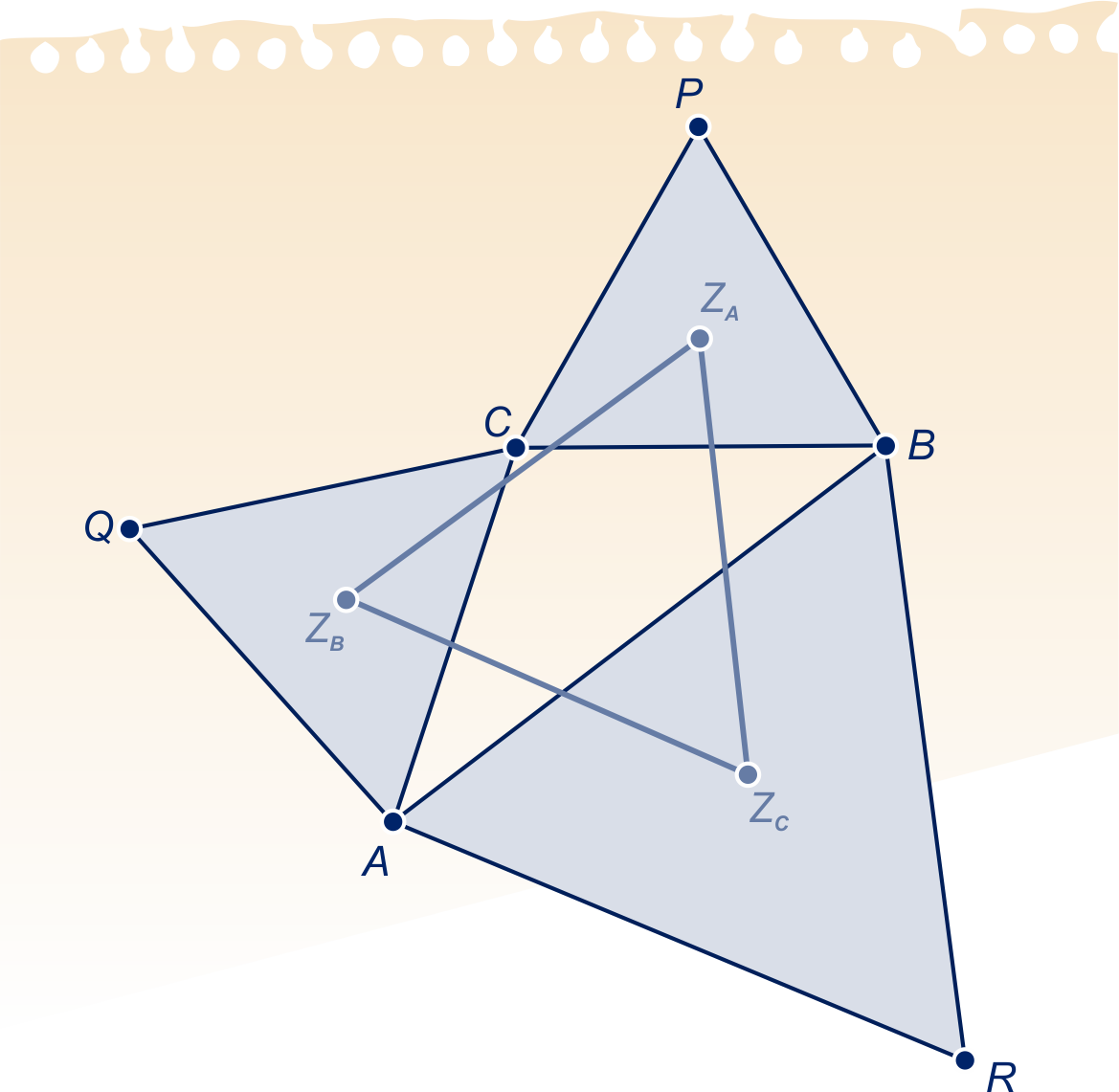
De stelling van Napoleon
$A B C$ is een willekeurige driehoek. De driehoeken $P B C$ , $A Q C$ en $A B R$ zijn gelijkzijdig met zwaartepunten $Z_{A}$ , $Z_{B}$ en $Z_{C}$ .
Dan is driehoek $Z_{A} Z_{B} Z_{C}$ gelijkzijdig.

Bewijs de stelling met een berekening met complexe getallen.

(hint)

Gebruik opgave 53.