kleiner

groter

Noem die hoek α, dan $\tan \text{α}=\frac{HD}{BD}=\frac{1}{2}\sqrt{2}$, dus $\text{α}=35°$.

in de richting van de snijlijn

in de richting van de vouwlijn

-

-

Zie figuur hieronder.

figuur bij opgave 45

figuur bij opgave 46

$35°$

waar ; waar ; waar

tussen $0°$ en $90°$.

Zie figuur hieronder.

$35°$

Zie figuur. Noem de gevraagde hoek α. Neem aan dat $P$ het midden van het grondvlak is en $Q$ het midden van het bovenvlak, dan $\tan \left(\text{α}\right)=\frac{PQ}{AP}=\sqrt{2}$ , dus de gevraagde hoek is $55°$.

Als $P$ het midden van $HF$ en $Q$ van $MN$, dan is het hoek $PQG$, die is $55°$.

figuur bij opgave 48a

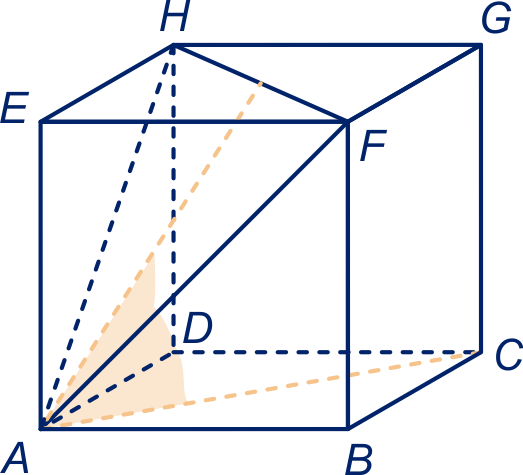
figuur bij opgave 49a

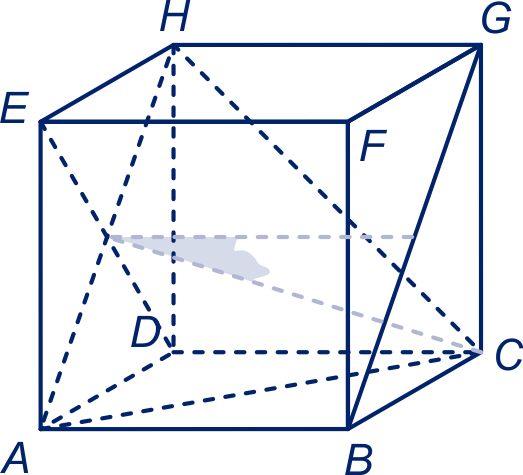
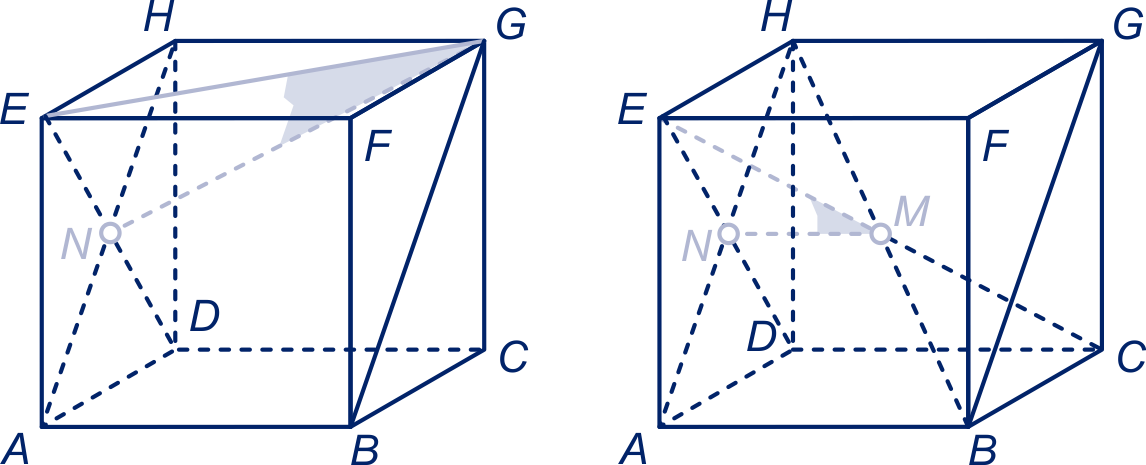
Zie figuur. Het midden van vierkant $ABCD$ noemen we $P$ en het midden van $BC$ noemen we $Q$, dan is de gevraagde hoek $2\cdot {\tan }^{\mathrm{‐}1}\left(\frac{PQ}{PT}\right)=2\cdot {\tan }^{\mathrm{‐}1}\left(\frac{1}{\sqrt{2}}\right)$, dus de gevraagde hoek is $71°$.

Zie figuur. Het midden van ribbe $DT$ noemen we $M$ en het midden van vierkant $ABCD$ is $P$. Dan is $2\cdot {\tan }^{\mathrm{‐}1}\left(\frac{PA}{PM}\right)=2\cdot {\tan }^{\mathrm{‐}1}\left(\sqrt{2}\right)$ de gevraagde hoek, dus $109°$.

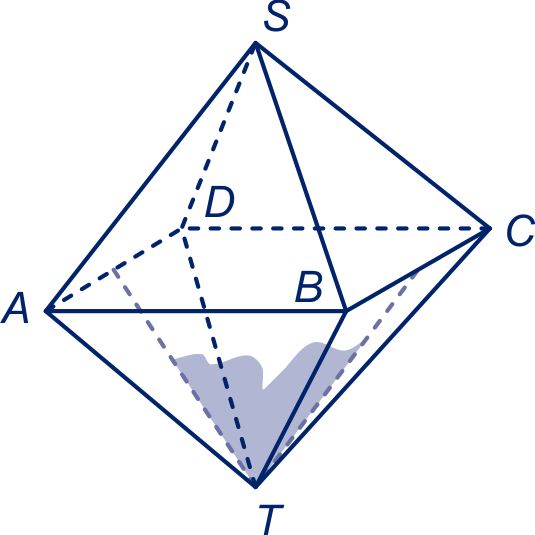
figuur bij opgave 50a

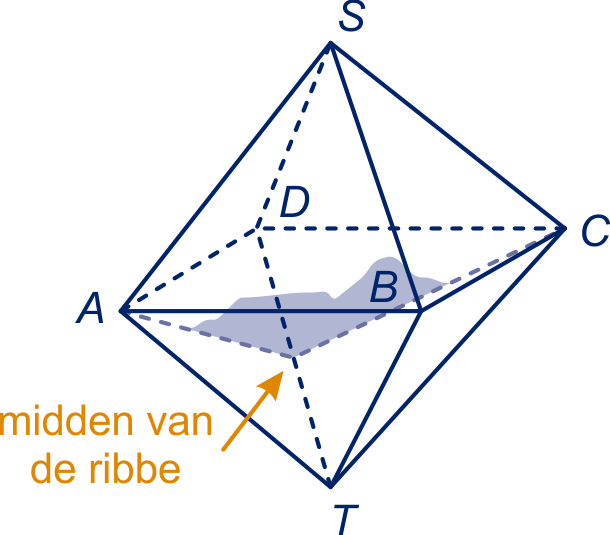
figuur bij opgave 50b

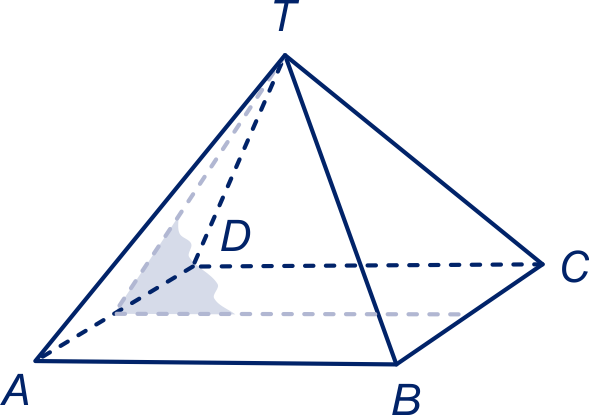
Neem het regelmatige viervlak heeft hoekpunten $A$, $B$, $C$ en $D$ en de ribben hebben lengte $2$. Het midden van $AB$ noemen we $M$, dan is de standhoek hoek $CMD$. De driehoek $CMD$ is gelijkbenig met zijden $MC=MD=\sqrt{3}$ en $CD=2$. Noem de standhoek α dan is $\sin \left(\frac{1}{2}\text{α}\right)=\frac{1}{\sqrt{3}}$, dus α$=71°$.

De hoek uit opgave 51a  is samen met de hoek uit opgave 50b $180°$.

De driehoeken $EBP$ en $HBE$ zijn gelijkvormig (beide driehoeken hebben hoek $B$ gemeenschappelijk en beide hebben een rechte hoek). Dus: $\frac{BP}{BE}=\frac{BE}{BH}$, dus $BP=4\sqrt{3}$. Dus $BP:HP=2:1$.

Het midden van $EG$ noemen we $M$. De zijden van driehoek $EMP$ zijn dan $\sqrt{6}$, $2\sqrt{6}$ en $3\sqrt{2}$, dus $EMP$ is een $30-60-90$-graden driehoek, de gevraagde hoek is dus exact $120°$.

$\frac{1}{2}\cdot \frac{1}{3}\cdot 8\sqrt{2}\cdot 8\sqrt{2}\cdot 8\sqrt{2}=170\frac{2}{3}\sqrt{2}$

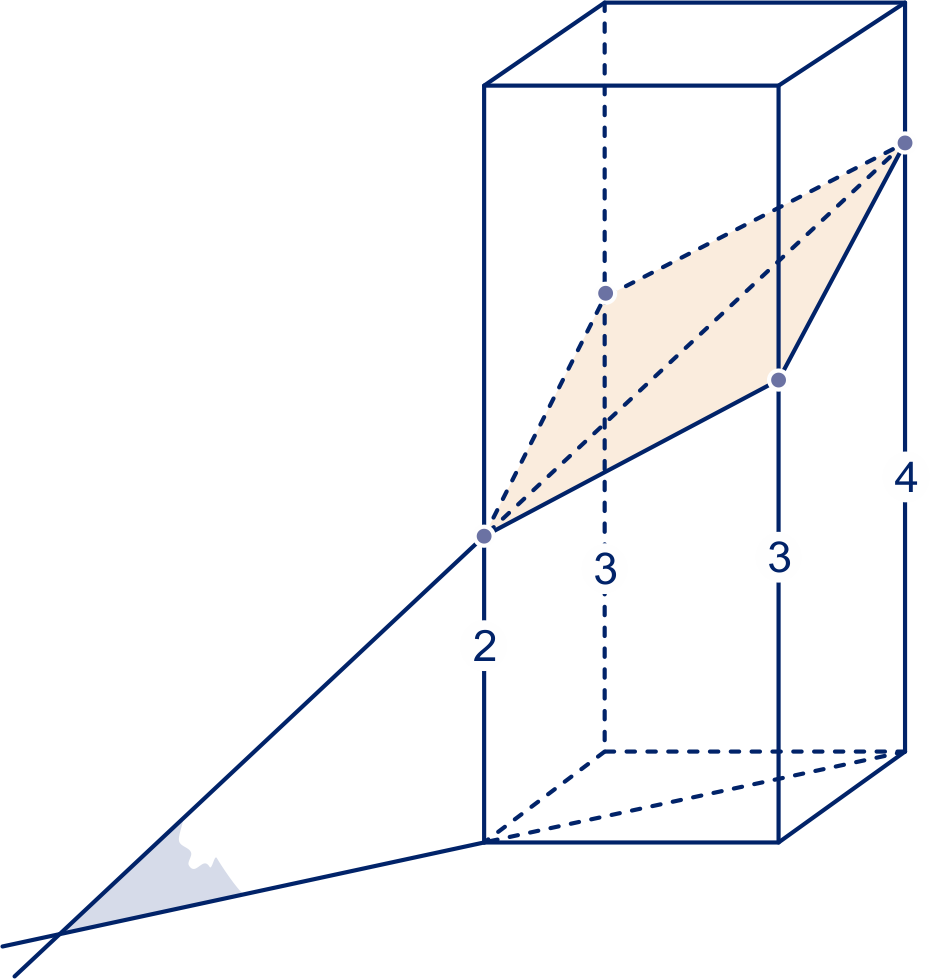
De oppervlakte van het grondvlak is $8\cdot 8\sqrt{3}=64\sqrt{3}$. Noem de gevraagde hoogte $h$, dan $\frac{1}{3}h\cdot 64\sqrt{3}=\frac{512}{3}\sqrt{2}$, dus $h=\frac{8}{3}\sqrt{6}$.

Noem de top van het bouwsel $T$, het midden van de lange zijde van een geodriehoek $M$ en de projectie van de top op het grondvlak $P$, dan is de gevraagde hoek de hoek $TMP$. Noem die α, dan $\sin \text{α}=\frac{h}{8}$, dus $\text{α}=$${\sin }^{\mathrm{‐}1}\left(\frac{1}{3}\sqrt{6}\right)=55°$.

Zie de figuur hieronder links.

Zie de figuur hieronder rechts.

$4°$, $86°$

Zie de figuur links. α is hoek $NGE$; die hoek is $30°$, want driehoek $DEG$ is gelijkzijdig.

Zie de figuur rechts. β is hoek $EMN$. Ergeldt: $\tan \left(\text{β}\right)=\frac{EN}{MN}=\sqrt{2}$, dus $\text{β}\approx$$55°$.

figuren bij opgave 56

$x+y+z=6$.

$\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$ is een richtingvector van lijn $MN$, dus $N=\left(3+t\mathrm{,6}+t\mathrm{,6}+t\right)$. Invullen in een vergelijking van $V$ geeft $t=\mathrm{‐}3$, dus $N=\left(\mathrm{0,3,3}\right)$.

$\sin \left(\text{α}\right)=\frac{MN}{AM}=\frac{3\sqrt{3}}{9}=\frac{1}{3}\sqrt{3}$, dus $\text{α}={\sin }^{\mathrm{‐}1}\left(\frac{1}{3}\sqrt{3}\right)=35°$.

Een normaalvector van vlak $ABHG$ is $\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right)$ en een normaalvector van vlak $ACH$ is $\overrightarrow{f}=\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$. Noem de hoek tussen die twee vectoren α, dan $\cos \left(\text{α}\right)=\frac{\overrightarrow{e}\cdot \overrightarrow{f}}{\sqrt{2}\cdot \sqrt{3}}=\frac{1}{3}\sqrt{6}$, dus (in graden nauwkeurig) $\text{α}=35°$.

Normaalvectoren van de vlakken zijn $\overrightarrow{f}=\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$ en $\overrightarrow{x}=\left(\begin{array}{c}1\\ 0\\ 2\end{array}\right)$. Noem de hoek tussen de vectoren β, dan $\cos \left(\text{β}\right)=\frac{\overrightarrow{x}\cdot \overrightarrow{f}}{\sqrt{5}\cdot \sqrt{3}}=\frac{1}{5}\sqrt{15}$, dus $\text{β}=39°$.

Noem die hoeken achtereenvolgens α, β en γ.
$\cos \left(\text{α}\right)=\frac{\overrightarrow{BA}\cdot \overrightarrow{BC}}{\left|\overrightarrow{BA}\right|\cdot \left|\overrightarrow{BC}\right|}=\frac{1}{10}\sqrt{10}$, dus $\text{α}=72°$;
$\cos \left(\text{β}\right)=\frac{\overrightarrow{TB}\cdot \overrightarrow{TC}}{\left|\overrightarrow{TB}\right|\cdot \left|\overrightarrow{TC}\right|}=\frac{31}{\sqrt{43}\cdot \sqrt{29}}$, dus $\text{β}=29°$;
$\cos \left(\text{γ}\right)=\frac{\left|\overrightarrow{TB}\cdot \overrightarrow{OC}\right|}{\left|\overrightarrow{TB}\right|\cdot \left|\overrightarrow{OC}\right|}=\frac{3}{\sqrt{43}}$ ,dus $\text{γ}=63°$.

Dat is de hoek die $\overrightarrow{BT}$ met $\overrightarrow{OT}$ maakt. Die is: $\mathrm{40,3}°$

Vlak $TAB$ is evenwijdig met de $y$-as en snijdt de andere coördinaat-assen in $\left(\mathrm{6,0,0}\right)$ en $\left(\mathrm{0,0,10}\right)$. Een vergelijking van vlak $TAB$ is dus: $\frac{x}{6}+\frac{z}{10}=1$, dus een normaalvector: $\overrightarrow{p}=\left(\begin{array}{c}5\\ 0\\ 3\end{array}\right)$.
Een vergelijking van vlak $TBC$ is: $\frac{x}{\mathrm{‐}12}+\frac{y}{4}+\frac{z}{10}=1$, dus een normaalvector is $\overrightarrow{q}=\left(\begin{array}{c}\mathrm{‐}5\\ 15\\ 6\end{array}\right)$. De hoek tussen de vlakken noemen we δ, dan $\left|\overrightarrow{p}\right|\cdot \left|\overrightarrow{q}\right|\cdot \cos \left(\delta \right)=\left|\overrightarrow{p}\cdot \overrightarrow{q}\right|$, dus $\text{δ}=86°$.

$2y-3z=0$ en $3x-4y=0$

Noem de gevraagde hoek α. Lijn $BC$ heeft richtingsvector $\left(\begin{array}{c}4\\ 3\\ \mathrm{‐}4\end{array}\right)$ en vlak $OAB$ heeft normaalvector ,$\left(\begin{array}{c}0\\ 2\\ \mathrm{‐}3\end{array}\right)$, dan $\left(\begin{array}{c}4\\ 3\\ \mathrm{‐}4\end{array}\right)\cdot \left(\begin{array}{c}0\\ 2\\ \mathrm{‐}3\end{array}\right)=\left|\left(\begin{array}{c}4\\ 3\\ \mathrm{‐}4\end{array}\right)\right|\cdot \left|\left(\begin{array}{c}0\\ 2\\ \mathrm{‐}3\end{array}\right)\right|\sin \left(\text{α}\right)$, dus $\sin \left(\text{α}\right)=\frac{18}{\sqrt{41}\cdot \sqrt{13}}$. De gevraagde hoek is dus $51°$.

Noem de gevraagde hoek β, dan is β de hoek tussen de vectoren $\left(\begin{array}{c}0\\ 2\\ \mathrm{‐}3\end{array}\right)$ en $\left(\begin{array}{c}\mathrm{‐}3\\ 4\\ 0\end{array}\right)$, dus $\left(\begin{array}{c}\mathrm{‐}3\\ 4\\ 0\end{array}\right)\cdot \left(\begin{array}{c}0\\ 2\\ \mathrm{‐}3\end{array}\right)=\left|\left(\begin{array}{c}\mathrm{‐}3\\ 4\\ 0\end{array}\right)\right|\cdot \left|\left(\begin{array}{c}0\\ 2\\ \mathrm{‐}3\end{array}\right)\right|\cos \left(\text{β}\right)$, dus $\cos \left(\text{β}\right)=\frac{8}{5\sqrt{13}}$. De gevraagde hoek is $64°$

$\frac{18}{13}\sqrt{13}$

$\text{cos}\left(\text{α}\right)=\frac{\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)\cdot \left(\begin{array}{c}4\\ 3\\ 2\end{array}\right)}{\sqrt{29}}=\frac{4}{\sqrt{29}}$; uit ${\sin }^2\left(\text{α}\right)+{\cos }^2\left(\text{α}\right)=1$ volgt dan dat $\sin \left(\text{α}\right)=\sqrt{\frac{13}{29}}$.

Oppervlakte driehoek $OAB=\frac{1}{2}\cdot OA\cdot OB\cdot \sin \left(\text{α}\right)=\frac{1}{2}\cdot 6\cdot \sqrt{29}\cdot \sqrt{\frac{13}{29}}=3\sqrt{13}$.

De inhoud van viervlak $OABC=\frac{1}{3}\cdot 3\sqrt{13}\cdot \frac{18}{13}\sqrt{13}=18$.