Het is de hoek α tussen de vectoren en . Dus en .
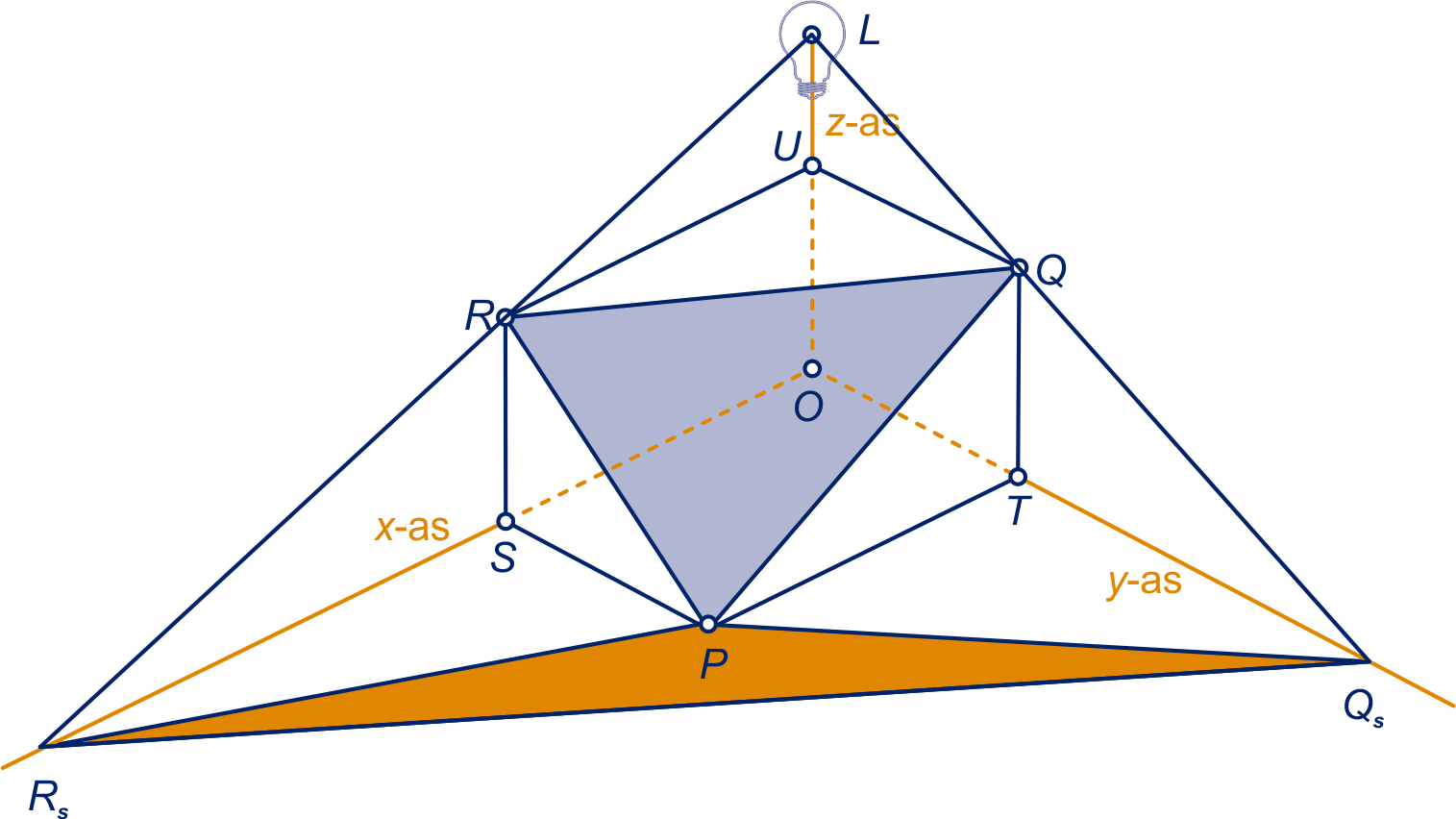
Het snijpunt van lijn met de
-as is en
het snijpunt van lijn met de
-as is ,
De schaduw is driehoek .
Uit gelijkvormigheid volgt: en .
Dus oppervlakte driehoek ,
oppervlakte driehoek ,
oppervlakte vierhoek ,
oppervlakte driehoek .
Dus oppervlakte schaduw is .
Teken een lijn door evenwijdig aan lijn . Die snijdt de ribbe . Het snijpunt noemen we . Lijn snijdt de -as in het gewenste punt .
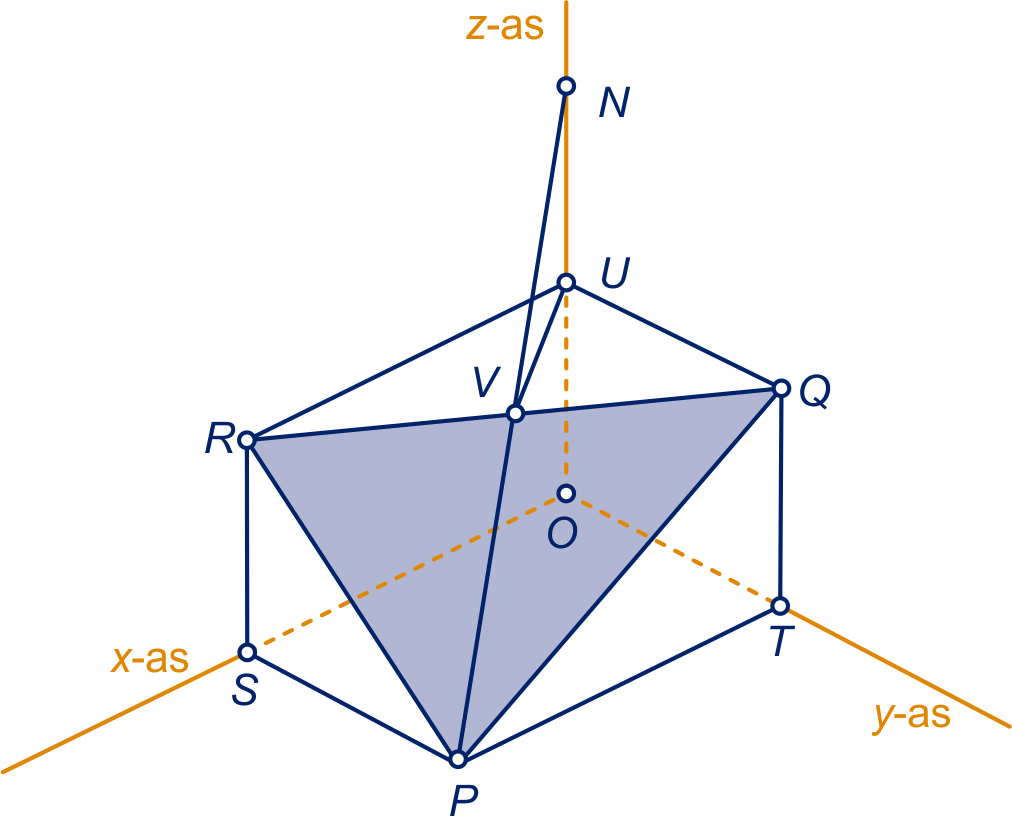
en
, dus
.
Die oppervlakte is .
Vlak heeft normaalvector , zie vorige onderdeel, dus een vergelijking is . Dit vlak snijdt d -as in .
en , dus
De oppervlakte van driehoek is
Noem die hoek α. Dan is de hoek tussen en
gelijk aan .
,
dus .
Lijn heeft pv
.
Een vergelijking van vlak is: . Dus
de waarde van die bij hoort is oplossing van de vergelijking:
, dus en
.
De inhoud van piramide is , dus de gevraagde inhoud is .
De doorsnede is vijfhoek , waarbij het snijpunt van de lijnen en is en het snijpunt van de lijnen en is en
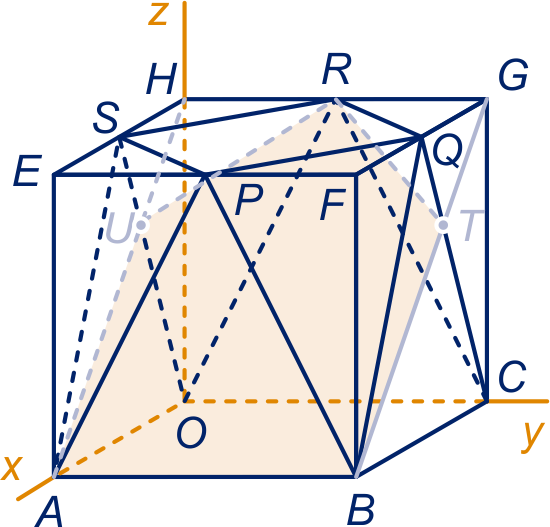
De driehoeken en
zijn gelijkvormig; de vergrotingsfactor is , dus
.
De oppervlakte van rechthoek ; de oppervlakte
van driehoek , De
oppervlakte van de doorsnede is .
Het vlak snijdt de -as in
, de
-as in
.
Een vergelijking is dus voor een of
ander getal . Het punt voldoet, dus
. Een vergelijking is dus:
.
Noem die hoek α, dan is α ook de hoek tussen de normaalvectoren en . We berekenen met het inproduct. Je vindt:, dus .
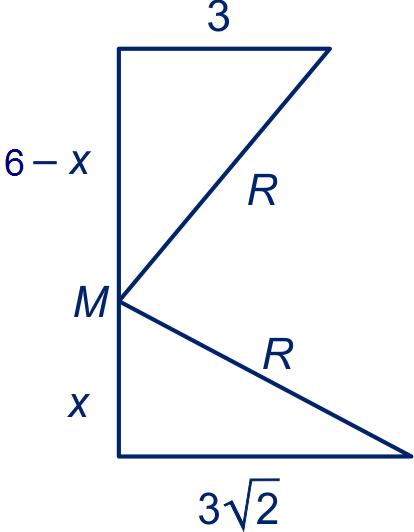
Het middelpunt van de bol ligt op de lijn door de middens van het boven- en het grondvlak van de kubus. Zeg op hoogte .
De cirkel door de vier hoekpunten in het bovenvlak heeft straal , die door hoekpunten van het
grondvalk heeft straal .
Noem de straal van de bol , dan geldt:
en
, dus
, dus het middelpunt is
.
De achthoek op hoogte bestaat uit een vierkant van bij waaruit bij de hoekpunten rechthoekige driehoeken met rechthoekszijden zijn weggelaten. De oppervlakte van de achthoek is dus , dus .
Kies een assenstelsel zó, dat de drie ribben op de assen liggen. Het hoogste punt is dan de oorsprong . En vergelijking van het maaiveld is: oftewel: . De afstand van tot het maaiveld is dan .
Dat is de hoek tussen de vlakken en
, dus de hoek α van
de vectoren en
.
Dus , dus
.
Noem de hellingshoek β, dan zijn normaalvectoren van de dakvlakken en , dus , dus .
De coördinaten van het snijpunt van de lijnen en zijn (met gelijkvormigheid). Een tweede punt van de snijlijn is , dus de snijlijn heeft pv: .
is het snijpunt van lijn met het vlak
door loodrecht op lijn . Een vergelijking van
is: .
Een pv van lijn is:
.
Je krijgt voor de waarde van waarvoor
, dus
voor . Je vindt:
.
is het snijpunt van lijn met het vlak
door loodrecht op lijn . Een vergelijking van
is: .
Een pv van lijn is:
.
Je krijgt voor de waarde van waarvoor
, dus
.
Dat is een stompe hoek. Normaalvectoren van de vlakken en zijn en . Noem de hoek α, dan en , dus de gevraagde hoek is .
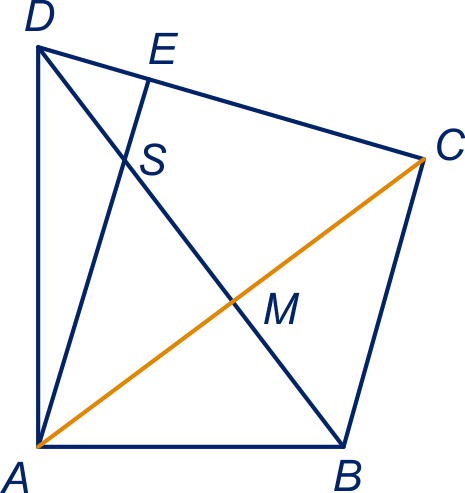
Druk de vlakken en
'plat'. De kortste weg is lijnstuk
in de platte figuur.
is het snijpunt van de lijnstukken
en . Er geldt:
(beide tweemaal de oppervlakte van driehoek
,
dus
en
.
staat loodrecht op
. Dus
is het snijpunt van het vlak loodrecht op met lijn .
Een pv van lijn is , een vergelijking van
is: .
Het snijpunt krijg je voor , dus dit is:
.
Zie figuur. De kortste weg is lijnstuk , waarbij
loodrecht op staat.
Hoek noemen we γ. Dan
en dus
, dus en
.
De gevraagde hoek is hoek , waarbij de punten , en in de 'ruimte' liggen. De zijden van driehoek zijn , en . De gevraagde hoek is: .
