Afbraak van penicilline
Ter bestrijding van een infectie begint een patiënt aan
een penicillinekuur die bestaat uit het innemen van pillen.
Iedere keer na het innemen van een pil stijgt de
concentratie penicilline in het bloed met eenheden
per milliliter. Aan het begin van de kuur zit er geen
penicilline in het bloed van de patiënt. De penicilline
wordt afgebroken met een snelheid die evenredig is met
de concentratie:
.
Hierbij is
de tijd (in uren) en de concentratie penicilline
(in eenheden per milliliter). De concentratie penicilline
mag niet onder de eenheden per milliliter
komen
Bereken hoeveel uur na het innemen van de eerste pil de tweede, derde en vierde pil moeten worden ingenomen. Geef je antwoorden in gehele uren.

Radioactief verval
Een manier om de ouderdom van organisch materiaal
vast te stellen is de zogenaamde koolstof-14 methode. In
levende organismen zit koolstof-12 en koolstof-14 in een
vaste verhouding. Zodra het organisme sterft, vervalt het
radioactieve koolstof-14. Het gehalte koolstof-14 noemen
we (in procenten van de oorspronkelijke hoeveelheid),
de tijd rekenen we in jaren vanaf het moment van sterven
van het organisme.
De groeisnelheid van is evenredig met zelf.
De evenredigheidsconstante noemen we .
Welke differentiaalvergelijking volgt hieruit voor ?
Is de evenredigheidsconstante in de differentiaalvergelijking positief of negatief?
Wat is de beginwaarde van ?
Stel een formule op voor uitgedrukt in .
De halfwaardetijd is de tijd waarin wordt gehalveerd. Voor koolstof-14 is de halfwaardetijd jaar.
Bereken .

Liften
Een student lift elke dag naar de
universiteit. De ene dag heeft hij snel een lift, de andere
dag duurt dat langer. De kans dat hij langer dan minuten
moet wachten om een lift te krijgen, noemen we .
Leg uit dat .
Maak aannemelijk dat voor alle getallen en geldt:
.
Uit b volgt:
.
Dus met
.
De ervaring leert dat de wachttijd in een kwart van de gevallen
langer is dan minuten.
Geef een formule voor .
Luchtdruk
De luchtdruk (in pascal) is gelijk aan het gewicht van de kolom lucht die zich boven een vierkante meter oppervlak
bevindt. Volgens de wet van Boyle is de snelheid waarmee de luchtdruk afneemt bij toenemende hoogte boven
het zeeniveau evenredig met de luchtdruk.
Dit leidt tot de differentiaalvergelijking
waarbij
de luchtdruk in hectopascal is en
de hoogte boven het zeeniveau in meters.
De luchtdruk op zeeniveau is hectopascal en op
km boven het zeeniveau
hectopascal.
Bepaal de hoogte met luchtdruk hectopascal.

In elk punt van de grafiek van de functie
hiernaast
geldt: de raaklijn in aan de grafiek van snijdt de
-as in
en de -as in
en is het midden van lijnstuk
.
Gegeven is de differentiaalvergelijking: .
Laat zien dat oplossingsfunctie is van de differentiaalvergelijking.
Toon aan dat de functies , waarbij een willekeurig getal is, oplossingsfuncties zijn van de differentiaalvergelijking
Teken op de GR de grafiek van een oplossingsfunctie die door gaat.

Algen
In een poel leeft een algenpopulatie. De hoeveelheid algen
die in de poel kan leven kent een natuurlijke bovengrens,
zeg . Hierdoor vindt geremde groei plaats.
Noem de omvang van de algenpopulatie op dag ,
uitgedrukt in procenten van . De groei
wordt geremd doordat in de poel visjes leven die algen
eten. Hierdoor verdwijnt een constante hoeveelheid algen
per dag uit de poel. Er geldt nu: ,
waarbij en positieve constanten
zijn. Neem aan dat ,
en .
Benader met de methode van Euler. Neem als stapgrootte. Geef je antwoord in twee decimalen nauwkeurig.
Bereken uit de gegeven differentiaalvergelijking op
welk percentage van de algenpopulatie zich zal stabiliseren.
Geef je antwoord in twee decimalen nauwkeurig.
Gegeven is de differentiaalvergelijking .
is de oplossingsfunctie met .
Geef een formule voor .
Hoe kun je aan de differentiaalvergelijking zien dat een buigpunt van de grafiek van is?
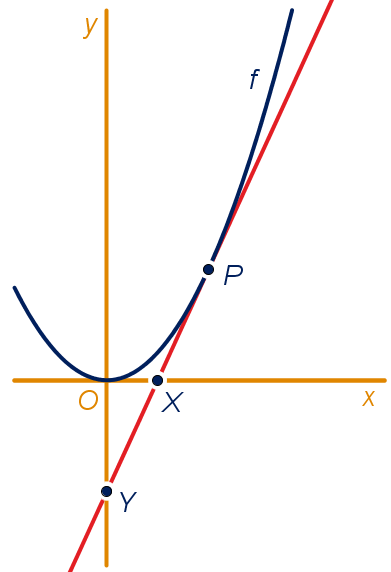
In elk punt van de grafiek van de functie hiernaast
geldt: de raaklijn in aan de grafiek van snijdt de
-as
in en de -as in
, dat het midden van lijnstuk
is.
Gegeven is de differentiaalvergelijking:
.
Laat zien dat oplossingsfunctie is van de differentiaalvergelijking.
Oplossingsfuncties zijn kwadratische functies met top .
Toon dat aan.

Glas
In de glastuinbouw is bekend dat licht aan intensiteit verliest
wanneer het door een glasplaat valt. De afstand die
het licht door het glas aflegt in mm noemen we en de
intensiteit die voldoet aan de differentiaalvergelijking
.
Hierbij is de uitdovingscoëfficiënt.
Een glasplaat van mm dik laat % van het (loodrecht)
erop vallende licht door.
Bereken .

De Italiaan Volterra (1860-1940) heeft wiskundige modellen
opgesteld die gebruikt worden bij populatievoorspellingen
in de biologie. In een van deze modellen ging
hij uit van twee vissoorten: roofdieren en
prooidieren in een zeker gebied.
Volterra nam aan dat bij afwezigheid van roofdieren, het
aantal prooidieren exponentieel zou toenemen, dus:
,
waarbij een evenredigheidsconstante is.
Als er wel roofdieren zijn, zal de factor afhankelijk zijn
van het aantal roofdieren: hoe groter het aantal roofdieren,
hoe kleiner de factor .
Volterra ging uit van een lineair verband:
.
Dit geeft de differentiaalvergelijking:
.
Op dezelfde manier vond hij voor de groei van het aantal roofdieren:
.
We kiezen ,
,
en .
Verklaar waarom genomen moet worden.
Op een gegeven moment zijn er roofdieren en prooidieren.
Geef een schatting van het aantal prooidieren en het aantal roofdieren tijdseenheid later.
Bij welk aantal prooi- en roofdieren zullen beide populaties volgens dit model constant blijven?
We bekijken opnieuw de differentiaalvergelijking bij de mottenbal uit
opgave 21: .
We definiëren de functies door
.
Hieronder staan de grafieken van voor
.
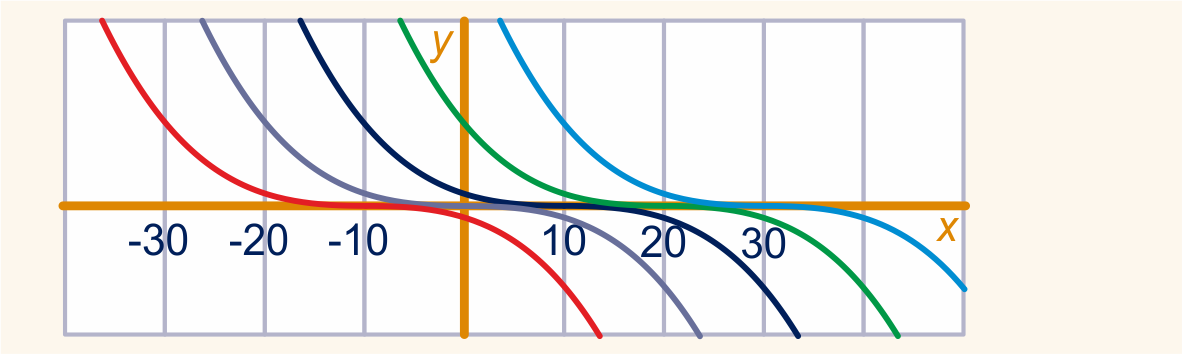
Laat zien dat de functies oplossingsfunctie van de differentiaalvergelijking zijn.
Ga na dat de nulfunctie (dat is de functie die constant de waarde heeft) ook een oplossing is.
En er zijn nog meer oplossingen. Bijvoorbeeld de functie
die ontstaat door een stuk van bijvoorbeeld in het snijpunt met de
-as aan een
stuk van de nulfunctie te 'plakken':
.
En deze functie beschrijft voor precies het gewicht van de
mottenbal van opgave 21 als functie van de tijd . Op
tijdstip wordt het gewicht en blijft het !
Bij deze differentiaalvergelijking gaan er door alle punten
van de -as meer dan één oplossingsfunctie. In deze
punten kun je van de ene oplossingsfunctie "overstappen"
op de andere. Er zijn dus meerdere oplossingen
van hetzelfde beginwaardeprobleem. Uit de context volgt
welke oplossingsfunctie het fysische proces beschrijft.
Gegeven is de differentiaalvergelijking .
Zoek een kwadratische functie die oplossing is van de differentiaalvergelijking.
Substitueer .
Links en rechts moet je dezelfde uitdrukking in krijgen.
