Hoofdstukken > Continue dynamische modellen

Differentiaalvergelijkingen

Een differentiaalvergelijking $\frac{d y}{d x} = c (x, y)$ schrijft in elk punt $(x, y)$ een richting voor: $c (x, y)$ .

Een functie die in elk punt van zijn grafiek de door de differentiaalvergelijking voorgeschreven richting (groeisnelheid) heeft, is een oplossingsfunctie van de differentiaalvergelijking.

Voorbeeld
Gegeven is de differentiaalvergelijking $\frac{d y}{d x} = \frac{2 y}{x} - 2$ .
Hier is dus $c (x, y) = \frac{2 y}{x} - 2$ . Een oplossingsfunctie van deze differentiaalvergelijking is bijvoorbeeld de functie
$f : x \to 2 x$ .
Dat kun je controleren door substitutie als volgt.
De richtingscoëfficiënt $\frac{d f}{d x}$ (groeisnelheid) van de functie $f$ is in elk punt $2$ . In elk punt van de grafiek van $f$ is de door de differentiaalvergelijking voorgeschreven richting: $\frac{2 y}{x} - 2 = \frac{2 \cdot 2 x}{x} - 2 = 2$ .
De functie $f$ heeft dus in elk punt van zijn grafiek de door de differentiaalvergelijking voorgeschreven richting.
Andere oplossingsfuncties zijn de functies $g_{c} : x \to c \cdot x^{2} + 2 x$ voor elke waarde van $c$ .
Enerzijds is de richtingscoëfficiënt van de functie $g_{c}$ in een punt $(x, y)$ van de grafiek $\frac{d g_{c}}{d x} = 2 c \cdot x + 2$ .
Anderzijds is de door de differentiaalvergelijking voorgeschreven richting in $(x, y)$ de richting $\frac{2 y}{x} - 2 = \frac{2 c x^{2} + 4 x}{x} - 2 = 2 c x + 2$ .
Deze zijn gelijk, dus zijn de functies $g_{c}$ oplossing van de differentiaalvergelijking.

Als er naast de differentiaalvergelijking ook een punt gegeven wordt dat op de grafiek van gezochte de oplossingsfunctie moet liggen, spreekt men van een beginwaardenprobleem.
Een oplossingsfunctie $h$ van de differentiaalvergelijking
$\frac{d y}{d x} = \frac{2 y}{x}$ met beginwaarde $h (1) = 10$ is: $h : x \to 8 \cdot x^{2} + 2 x$ .

Bij een gegeven differentiaalvergelijking kan een richtingsveld getekend worden. Hieronder is die bij de differentiaalvergelijking $\frac{d y}{d x} = \frac{2 y}{x} - 2$ getekend: de lijnstukjes hebben in elk punt de voorgeschreven richting.

De methode van Euler

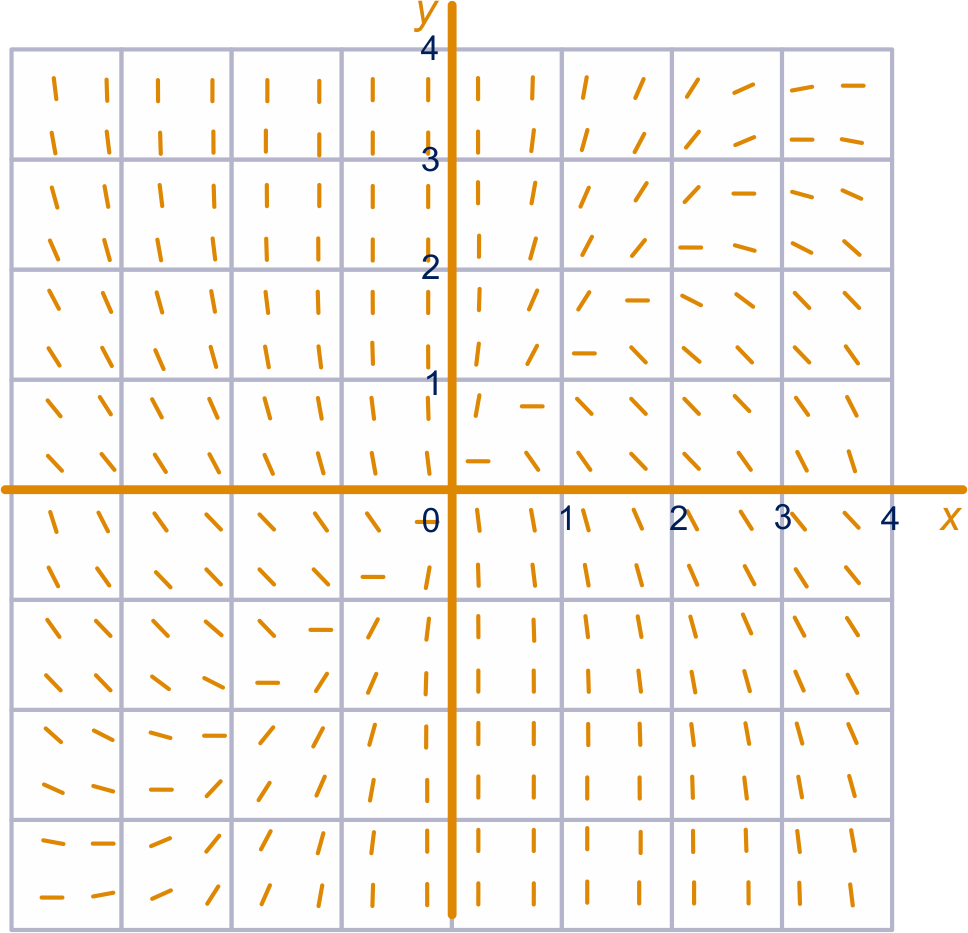
De oplossingsfunctie van de differentiaalvergelijking
$\frac{d y}{d x} = c (x, y)$ met beginwaarde $(p, q)$
kun je benaderen met een grafiek van punten die in de $x$ -richting op afstand $Δ$ van elkaar liggen met de methode van Euler.
Het zijn de punten $(a_{n}, b_{n})$ waarbij $(a_{0}, b_{0}) = (p, q)$ en
$a_{n + 1} = a_{n} + Δ$ en $b_{n + 1} = b_{n} + c (a_{n}, b_{n}) \cdot Δ$ .
Hoe kleiner $Δ$ , hoe beter de grafiek van de oplossingsfunctie benaderd wordt.

Ongeremde groei

De differentiaalvergelijking $\frac{d y}{d x} = c \cdot y$ hoort bij ongeremde groei. Hierbij is $c$ een willekeurige constante.
Oplossingsfuncties van deze differentiaalvergelijking zijn van de vorm $y = a \cdot e^{c \cdot x}$ , voor alle mogelijke waarden van $a$ .
Door elk punt van het vlak gaat een functie van deze vorm. Een oplossingsfunctie met domein $ℝ$ (de verzameling van alle reële getallen) is door zijn startpunt vastgelegd.

Logistische groei

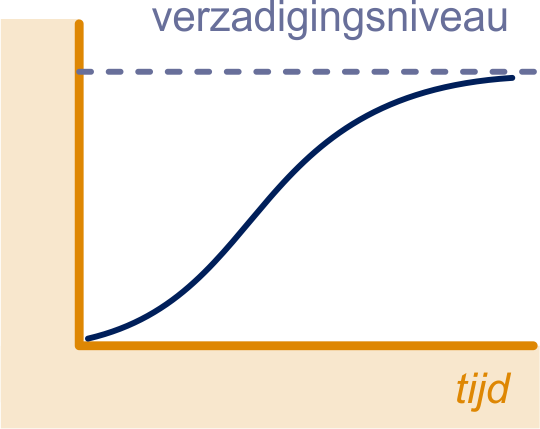
De hoeveelheid $y$ groeit logistisch met verzadigingsniveau $M$ als de groeisnelheid evenredig is met $y (M - y)$ , dus
$\frac{d y}{d t} = c \cdot y (M - y)$ voor een of ander positief getal $c$ .
De oplossingsfuncties van deze differentiaalvergelijking zijn: $y = \frac{M}{1 + b \cdot e^{‐ c M t}}$ .
Hierbij wordt $b$ bepaald door het beginwaarde van de oplossingsfunctie.
Een grafiek bij zo'n groei heeft een vorm zoals hiernaast getekend is.
Een logistische groeifunctie heeft een buigpunt. Dat ligt half zo hoog als het verzadigingsniveau.
Logistische groei bij de differentiaalvergelijking
$\frac{d y}{d t} = c \cdot y (M - y)$
is aanvankelijk nagenoeg exponentiëel met groeifactor $e^{c M}$ .