1

a

De overstaande hoeken zijn gelijk; twee aanliggende hoeken zijn samen $180 °$ .
De diagonalen delen elkaar midden door.

b

De zijden zijn even lang.
De diagonalen staan loodrecht op elkaar.

c

De hoeken zijn $90 °$ .
Die zijn even lang.

2

a

Een parallellogram.

b

Een rechthoek

3

a

Een rechthoek

b

Een vierkant

4

a

Nee

b

Ja

5

a

Nee

b

Ja

6

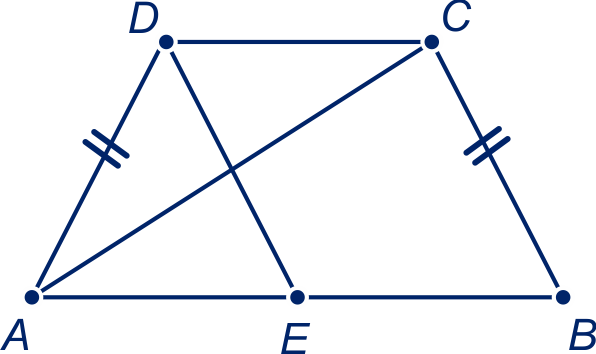
$A B C D$ is een gelijkbenig trapezium. Neem $E$ op $A B$ zó, dat $D E ∥ C B$ , dan is $E B C D$ een parallellogram.
Gegeven $| A D | = | B C |$ en $E B C D$ parallellogram.
Te bewijzen $| A C | = | B D |$
Bewijs

$1. ∠ D E A = ∠ C B E$	F-hoeken
$2. \| D E \| = \| C B \|$	$D E B C$ parallellogram
$3. \| D E \| = \| A D \|$	uit 2 en gegeven
$4. ∠ D A B = ∠ D E A$	uit 3
$5. ∠ D A B = ∠ C B A$	uit 1 en 4
$6. △ D A B ≅ △ C B A$	ZHZ, uit 5, gegeven en $\| A B \| = \| A B \|$

Het gevraagde volgt nu uit 6.

7

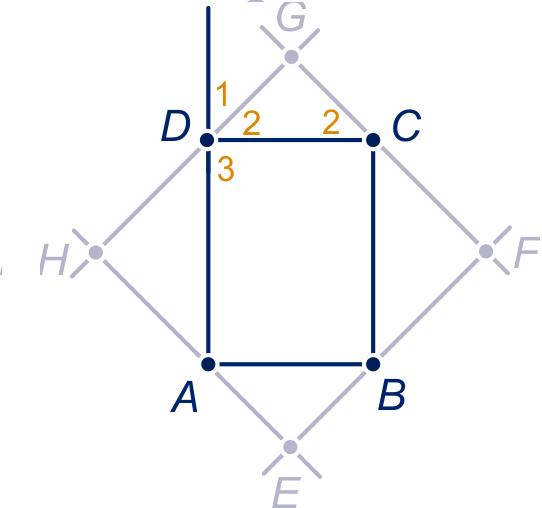
Opmerking In een gelijkbenige rechthoekige driehoek verhouden de zijden zich als $1 : 1 : \sqrt{2}$ .
Gegeven $A B C D$ rechthoek en $G H$ , $H E$ , $E F$ en $F G$ zijn buitenbissectricen.
Te bewijzen $E F G H$ is een vierkant.

$1. ∠ D_{1} = ∠ D_{2}$	buitenbissectrice
$2. ∠ D_{1} + ∠ D_{2} = 90 °$	$A B C D$ rechthoek
$3. ∠ D_{1} = ∠ D_{2} = 45 °$	uit 1 en 2
$4. ∠ C_{2} = 45 °$	zoals $∠ D_{2} = 45 °$
$5. ∠ G = 90 °$	uit 3 en 4
$6. △ D C G$ gelijkbenig rechthoekig	uit 3 en 4
$7. △ D H A$ gelijkbenig rechthoekig	net zo
$8. \| G H \| = \frac{1}{2} \sqrt{2} (\| A D \| + \| D C \|)$	Zie opmerking

Dat laatste geldt ook voor de andere zijden van vierhoek $E F G H$ en de hoeken zijn, net als hoek $G$ recht. Dus vierhoek $E F G H$ is een vierkant.

8

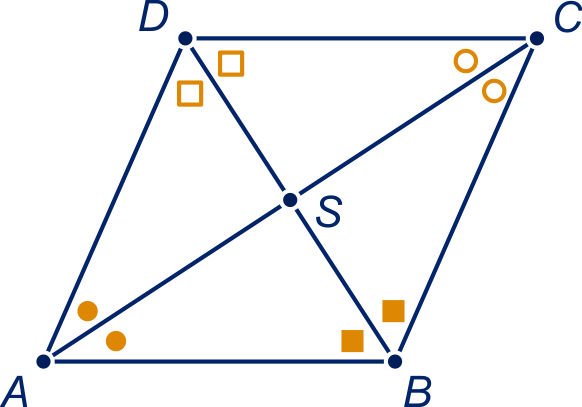
Gegeven In vierhoek $A B C D$ zijn de diagonalen bissectrices. (Dit is met gelijke symbolen aangegeven in de figuur.)
Tebewijzen $A B C D$ is een ruit.
Bewijs

$1. ∠ A C B = ∠ A C D$	gegeven
$2. ∠ C A B = ∠ C A D$	gegeven
$3. \| A C \| = \| A C \|$
$4. △ A B C ≅ △ A D C$	HZH uit 1, 2 en 3
$5. \| A B \| = \| A D \|$ en $\| B C \| = \| C D \|$	uit 4
$6. △ B C D ≅ △ B A D$	net zo
$7. \| B C \| = \| A B \|$	uit 6
$8.$ $A B C D$ ruit	uit 5 en 7

9

Gegeven vierhoek $A B C D$ met $A B$ en $C D$ evenwijdig en $| B C | = | A D |$ . Als $A D ∥ B C$ , dan is vierhoek $A B C D$ een parallellogram (definitie).
Als $A D$ en $B C$ niet evenwijdig zijn, is vierhoek $A B C D$ een gelijkbenig trapezium (definitie).

10

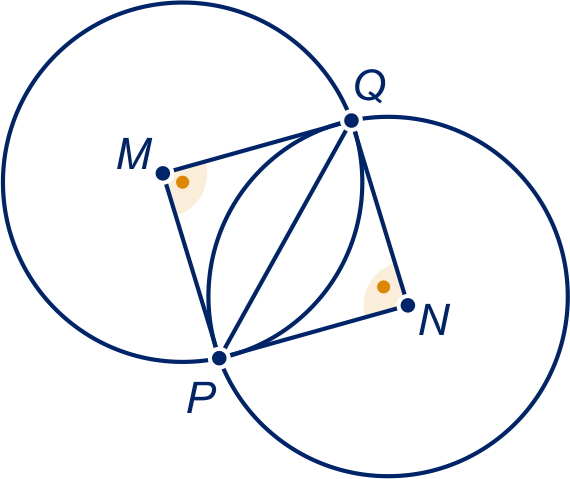
De driehoeken $P M Q$ en $P N Q$ zijn gelijkbenig en hebben dezelfde tophoek, dus hebben ze alle hoeken gelijk. Omdat beide dezelfde basis $P Q$ hebben, zijn ze congruent (HZH), dus hebben ze dezelfde straal.

11

Zie de figuur hieronder.

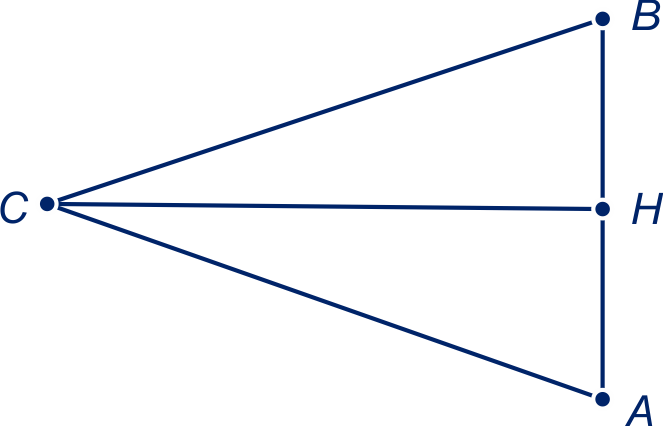
In driehoek $A B C$ geldt: $| A C | = | B C |$ en $H$ ligt op lijnstuk $A B$ zó, dat $C H ⊥ A B$ .
We bewijzen dat de driehoeken $A H C$ en $B H C$ congruent zijn.

$1. ∠ A H C = ∠ B H C$ $= 90 °$	$C H ⊥ A B$
$2. \| A C \| = \| B C \|$	gegeven
$3. \| H C \| = \| H C \|$
$4. △ A H C ≅ △ B H C$	uit 1, 2 en 3

Uit de congruentie volgt dat $∠ A C H = ∠ B C H$ , dus dat $C H$ bissectrice van driehoek $A B C$ is.
En ook dat $| A H | = | B H |$ , dus dat $C H$ middelloodlijn van driehoek $A B C$ is.
Merk op dat het middelpunt van de ingeschreven cirkel van een driehoek op elke bissectrice van de driehoek ligt en het middelpunt van de omgeschreven cirkel op elke middelloodlijn van de zijden van de driehoek.

12

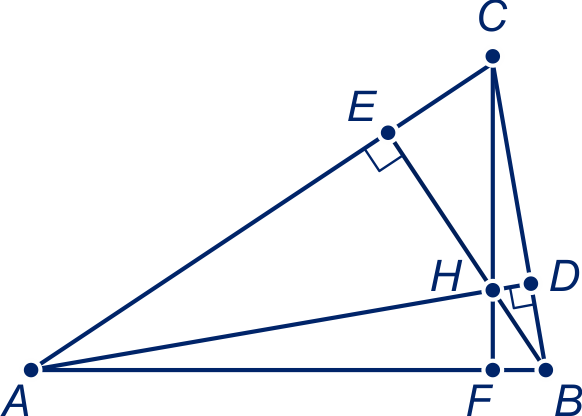
Gegeven: $A D$ , $B E$ en $C F$ hoogtelijnen van driehoek $A B C$ .
Dan zijn $B D$ , $A E$ en $H F$ de hoogtelijnen van driehoek $A B H$ .
Dus $C$ is het hoogtepunt van driehoek $A B H$ .

13

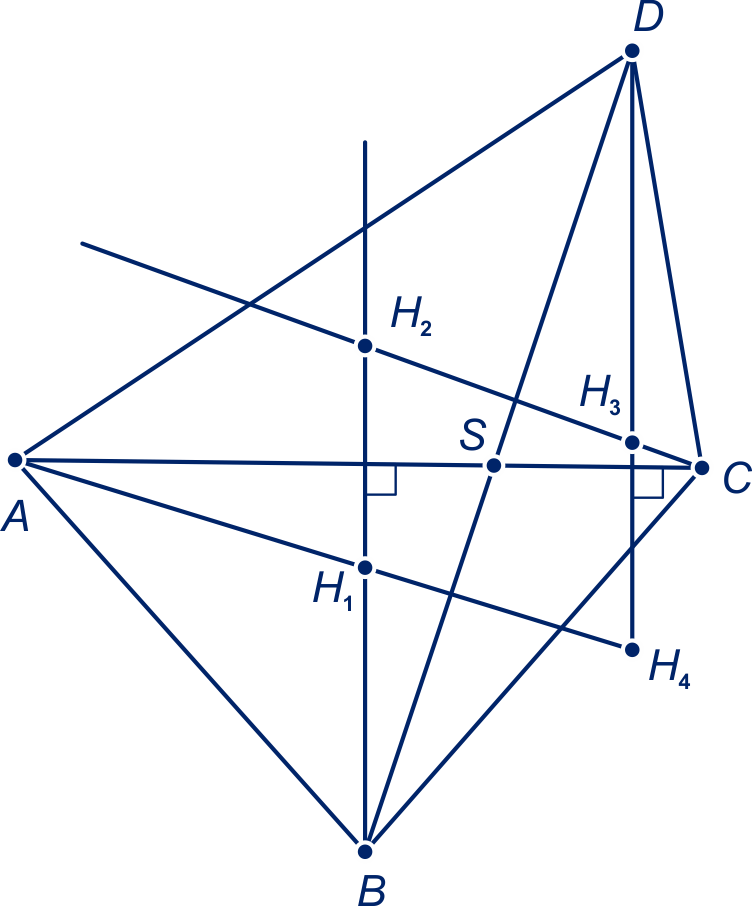
Het snijpunt van de diagonalen van de vierhoek $A B C D$ is $S$ .
Het hoogtepunt van driehoek $A B S$ is $H_{1}$ .
Het hoogtepunt van driehoek $B C S$ is $H_{2}$ .
Het hoogtepunt van driehoek $C D S$ is $H_{3}$ .
Het hoogtepunt van driehoek $D A S$ is $H_{4}$ .

$1. H_{1} H_{2} ⊥ A C$	gegeven
$2. H_{3} H_{4} ⊥ A C$	gegeven
$3. H_{1} H_{2} ∥ H_{3} H_{4}$	F-hoeken, uit 1 en 2
$4. H_{1} H_{4} ∥ H_{2} H_{3}$	net zo

Uit 3 en 4 volgt volgens definitie:
$5. H_{1} H_{2} H_{3} H_{4}$ parallellogram

14

a

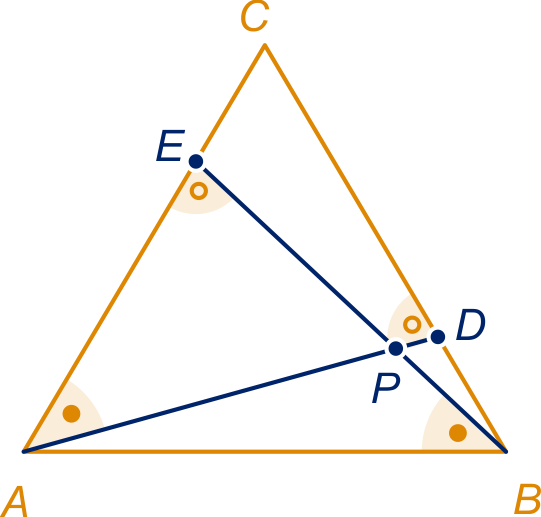
De driehoeken $A D C$ en $B E A$

$1. \| A C \| = \| A B \|$	gegeven
$2. \| C D \| = \| A E \|$	uit 1 en $\| B D \| = \| C E \|$
$3. ∠ A C D = ∠ B A E$	beide $60 °$
$4. △ A C D ≅ △ B A E$	ZHZ, uit 1, 2 en 3

b

$5. ∠ C A D = ∠ A B E$	uit 4
$6. ∠ A D C = ∠ B E A$	uit 4
$7. ∠ C A D + ∠ A D C$
$= 120 °$	hoekensom driehoek
$8. ∠ A E P + ∠ E A P$
$= 120 °$	uit 5, 6 en 7
$9. ∠ A P B = 120 °$	$A P B$ buitenhoek $△ A E P$

15

a

$b g (A C) = 180 °$ , want $A C$ is een middellijn van de cirkel.

b

$b g (A B) = \frac{1}{5} \cdot 360 ° = 72 °$ , $b g (A C) = \frac{2}{5} \cdot 360 ° = 144 °$

16

a

$| A B |$ met de cosinusregel:
$| A B |^{2} = 3^{2} + 3^{2} - 2 \cdot 3 \cdot \cos (129 °)$ , dus $| A B | \approx 5,42$ .
De lengte van boog $A B$ is $\frac{129}{360}$ van de cirkelomtrek, dus $\frac{129}{360} \cdot 2 π \cdot 3 \approx 6,75$

b

$| A B | = r \sqrt{2 - 2 \cos (α)} = 2 r \cdot \sin (\frac{1}{2} α) |$ ; de lengte van boog $A B$ is $\frac{α}{360} \cdot 2 π \cdot r = \frac{α \cdot π}{180} \cdot r$ .

17

Als $b g (A B) = b g (C D)$ , dan $∠ A M B = ∠ C M D$ , dus $△ A M B ≅ △ C M D$ (ZHZ), dus
$| A B | = | C D |$ .
Als | $| A B | = | C D |$ , dan $∠ A M B = ∠ C M D$ (ZZZ), dus $∠ A M B = ∠ C M D$ , dus
$b g (A B) = b g (C D)$ .