1

a

$11$ en $17$

b

$‐ 11$ , $‐ 17$ , $11$ , $17$

2

a

-

b

Als je linksom moet draaien is de hoek β tussen de vectoren $\vec{a}$ en $\vec{b}$ gelijk aan $90 ° - α$ en als je rechtsom moet draaien $α - 90 °$ . De oppervlakte van het parallellogram is $| \vec{a} | \cdot | \vec{b} | \sin (β)$ $= | \vec{a} | \cdot | {\vec{b}}_{R} | \sin (β)$ , want $\vec{b}$ en ${\vec{b}}_{R}$ hebben dezelfde lengte. In het eerste geval geldt: $\sin (β) = \cos (α)$ , in het tweede geval $\sin (β) = ‐ \cos (α)$ .

c

-

3

a

$| \begin{matrix} ‐ 1 & 3 \\ 3 & 2 \end{matrix} | = ‐ 11$ , dus de oppervlakte van het eerste is parallellogram is $11$ ; $| \begin{matrix} ‐ 1 & 5 \\ 3 & 2 \end{matrix} | = ‐ 17$ , dus de oppervlakte van het tweee is parallellogram is $17$ .

b

$\vec{A B} = (\begin{matrix} 6 \\ ‐ 4 \end{matrix})$ en $\vec{A C} = (\begin{matrix} 4 \\ 3 \end{matrix})$ ; $| \begin{matrix} 6 & 4 \\ ‐ 4 & 3 \end{matrix} | = 34$ , dus de oppervlakte van driehoek $A B C = 17$ .

c

De bijbehorende determinant (zoals in het vorige onderdeel) heeft twee kolommen met gehele getallen, is dus ook geheel.

4

a

$10$ , $14$ , $‐ 14$ en $0$

b

$‐ 2 \cdot 10 = ‐ 20$

c

$24$

d

$‐ 20$

5

a

Verbind het inwendig roosterpunt met de hoekpunten van de driehoek. Zo heb je de driehoek in drie roosterdriehoeken verdeeld die elk minstens oppervlakte $\frac{1}{2}$ hebben.

b

6

a

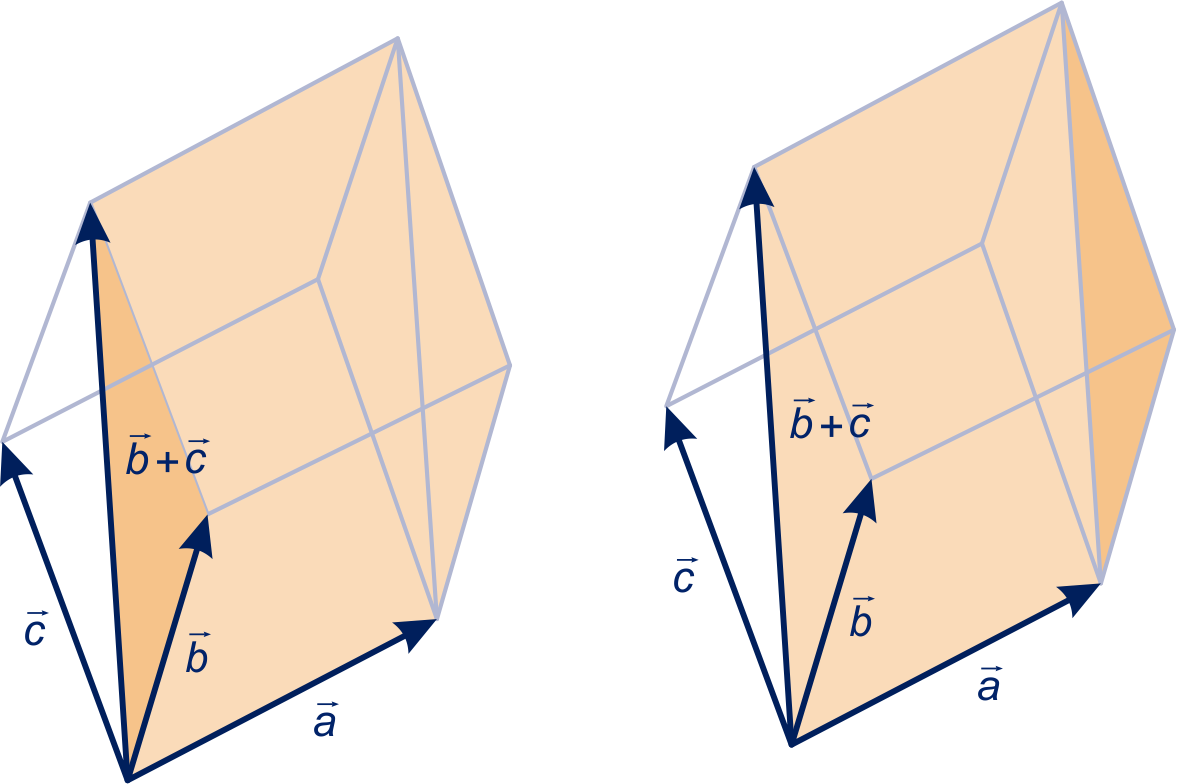
De twee licht gekleurde delen in de figuur links hebben samen oppervlakte $det (\vec{a}, \vec{b}) + det (\vec{a}, \vec{c})$ .
Het licht gekleurde parallellogram in de figuur rechts heeft oppervlakte $det (\vec{a}, \vec{b} + \vec{c})$ . Die twee zijn gelijk, want de donker gekleurde driehoeken links en rechts hebben dezelfde oppervlakte.

b

figuur bij opgave 79b

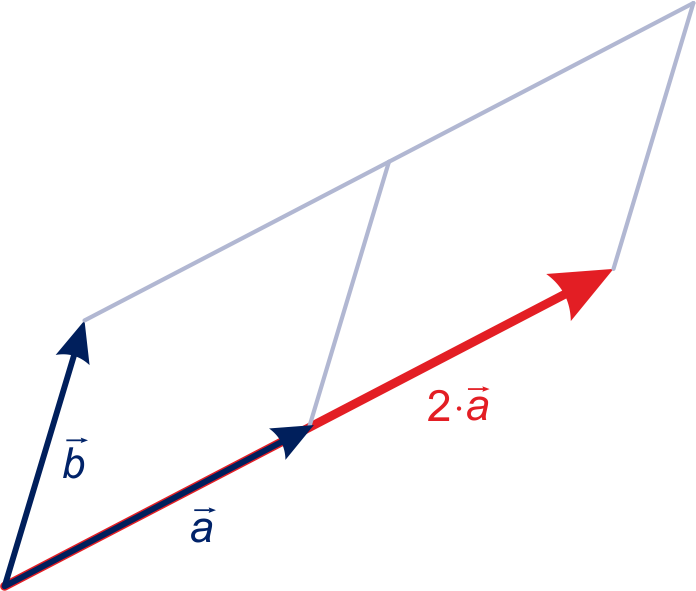
Het parallellogram bij de vectoren $2 \cdot \vec{a}$ en $\vec{b}$ heeft één zijde twee keer zo lang.

7

a

$det (\vec{a}, \vec{b}) =$ $det (a_{1} \cdot {\vec{e}}_{1} + a_{2} \cdot {\vec{e}}_{2}, \vec{b}) =$
$det (a_{1} \cdot {\vec{e}}_{1}, \vec{b}) + det (a_{2} \cdot {\vec{e}}_{2}, \vec{b}) =$
$a_{1} \cdot det ({\vec{e}}_{1}, \vec{b}) + a_{2} \cdot det ({\vec{e}}_{2}, \vec{b}) =$ ....
Maak het verder zelf af.

b

$({\vec{e}}_{1}, {\vec{e}}_{2})$ is positief georiënteerd en spant een vierkant van $1$ bij $1$ op; $det ({\vec{e}}_{1}, {\vec{e}}_{2}) = ‐ det ({\vec{e}}_{2}, {\vec{e}}_{1})$ ; verder $({\vec{e}}_{1}, {\vec{e}}_{1})$ en $({\vec{e}}_{2}, {\vec{e}}_{2})$ afhankelijk.

8

$C = (t,2 t + 7)$ ; dan $\vec{A B} = (\begin{matrix} 8 \\ ‐ 2 \end{matrix})$ en $\vec{A C} = (\begin{matrix} t + 3 \\ 2 t \end{matrix})$ . Dan $det (\vec{A B}, \vec{A C}) = \pm 30$ $\Leftrightarrow 18 t - 6 = \pm 30$ , dus $C = (5,10)$ of $C = (1 \frac{1}{2}, ‐ 3)$ .

9

Positief: $(\vec{a}, \vec{b}, \vec{c})$ , $(\vec{b}, \vec{c}, \vec{a})$ , $(\vec{c}, \vec{a}, \vec{b})$ ; de andere drie negatief.

10

a

Vergelijk dat met wat er in opgave 77 gedaan is.

b

$det ({\vec{e}}_{1}, {\vec{e}}_{1}, {\vec{e}}_{2}) = 0$ , want $({\vec{e}}_{1}, {\vec{e}}_{1}, {\vec{e}}_{2})$ is afhankelijk.
$det ({\vec{e}}_{1}, {\vec{e}}_{2}, {\vec{e}}_{3}) =$ $det ({\vec{e}}_{2}, {\vec{e}}_{3}, {\vec{e}}_{1}) =$ $det ({\vec{e}}_{3}, {\vec{e}}_{1}, {\vec{e}}_{2}) = 1$ en $det ({\vec{e}}_{1}, {\vec{e}}_{3}, {\vec{e}}_{2}) =$ $det ({\vec{e}}_{2}, {\vec{e}}_{1}, {\vec{e}}_{3}) =$ $det ({\vec{e}}_{3}, {\vec{e}}_{2}, {\vec{e}}_{1}) = ‐ 1$ : de zes rijtjes vectoren spannen een kubus met ribbe $1$ op; de eerste drie rijtjes vectoren hebben een positieve oriëntatie en de andere een negatieve.

c

Dit volgt direct uit de vorige twee onderdelen.

11

$2$ , $‐ 14$ , $‐ 51$

12

a

$\vec{A B} = (\begin{matrix} 2 \\ ‐ 2 \\ ‐ 1 \end{matrix})$ , $\vec{B C} = (\begin{matrix} 1 \\ ‐ 3 \\ ‐ 1 \end{matrix})$ en $\vec{A E} = (\begin{matrix} 0 \\ 0 \\ 10 \end{matrix})$ .
Van $A$ naar $H$ moet je schuiven over $\vec{B C} + \vec{A E}$ , dus $H = (3, ‐ 3,9)$ .

b

Het is de absolute waarde van de determinant $det (\vec{A B}, \vec{B C}, \vec{A E}) = | \begin{matrix} 2 & 1 & 0 \\ ‐ 2 & ‐ 3 & 0 \\ ‐ 1 & ‐ 1 & 10 \end{matrix} |$ .

c

$\frac{1}{6} \cdot 40 = 6 \frac{2}{3}$ ; ook $6 \frac{2}{3}$

13

De inhoud van het viervlak is $\frac{1}{6}$ van een parallellepipedum met roosterpunten als hoekpunt, dus de inhoud van het viervlak is minstens $\frac{1}{6}$ . Door het inwendig roosterpunt met de hoekpunten te verbinden, verdeel je het viervlak in vier viervlakken met inhoud minstens $\frac{1}{6}$ .

14

a

Dat is zo als $(\vec{a}, \vec{r}, \vec{s})$ , met $\vec{a} = (\begin{matrix} a \\ b \\ 2 \end{matrix})$ , afhankelijk is.

b

$a + b = 4$

c

$| \begin{matrix} a - 3 & 2 & 1 \\ b & 0 & 1 \\ 2 & 1 & 1 \end{matrix} | = 0$ , dus $a + b = 7$ .

15

a

$x + 4 y - 3 z = 0$

b

Vul maar in.

16

Schrijf links en rechts van het gelijkteken uit en constateer dat je detzelfde uitdrukkingen krijgt.

17

$(\begin{matrix} 5 \\ 2 \\ ‐ 3 \end{matrix})$ , $(\begin{matrix} 2 \\ 4 \\ 2 \end{matrix})$ , $(\begin{matrix} ‐ 1 \\ ‐ 10 \\ 7 \end{matrix})$

18

Dat is: $2 \cdot (| \vec{A B} \times \vec{B C} | + | \vec{A B} \times \vec{A E} | + | \vec{B C} \times \vec{A E} |) =$
$= 2 \cdot | (\begin{matrix} ‐ 1 \\ ‐ 1 \\ ‐ 4 \end{matrix}) | + 2 \cdot | (\begin{matrix} ‐ 20 \\ ‐ 20 \\ 0 \end{matrix}) | + 2 \cdot | (\begin{matrix} ‐ 30 \\ ‐ 10 \\ 0 \end{matrix}) |$ $= 46 \sqrt{2} + 20 \sqrt{10}$ .

19

$\vec{a} \times \vec{b}$ is normaalvector van $V$ en $\vec{c} \times \vec{d}$ is normaalvector van $W$ , dus
$\vec{r} = (\vec{a} \times \vec{b}) \times (\vec{c} \times \vec{d})$ , staat loodrecht op normaalvectoren van $V$ en $W$ , is dus richtingsvector van de snijlijn van $V$ en $W$ .